分析计算题解答详解

2.22 已知电阻电路如图2-49所示，R₁=15Ω，R₂=10Ω，R₃=3Ω，R₄=2Ω，试求各电路的等效电阻。

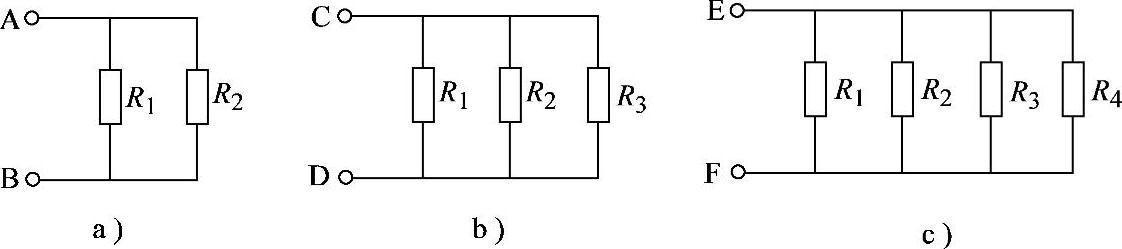
图2-49 习题2.22电路

解：（1）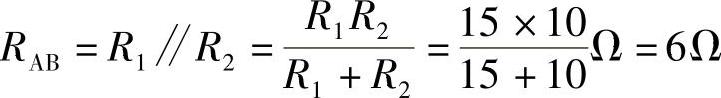

（2）

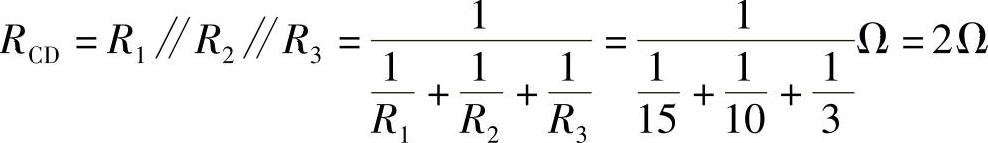
（3）

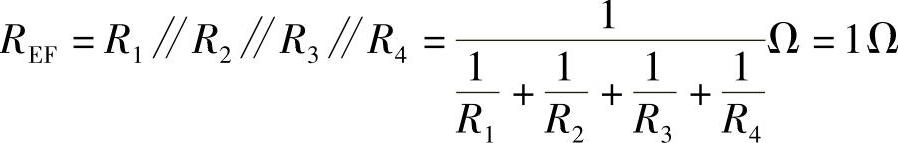
2.23 已知电阻电路如图2-50所示，试求各电路的ab端等效电阻。

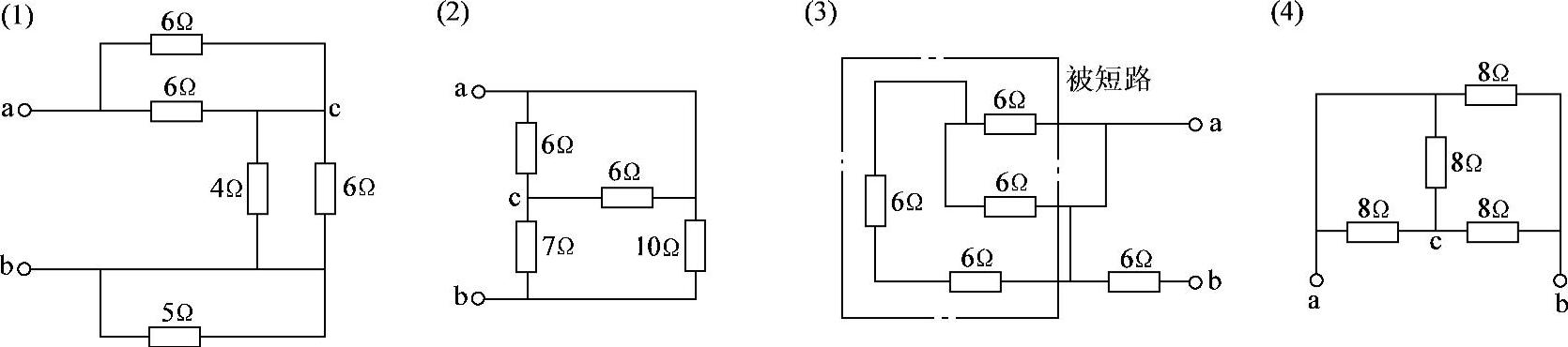
图2-50 习题2.23电路

解：分别画出图2-50所示各电路便于观察串并联结构的等效电路如图2-51所示。

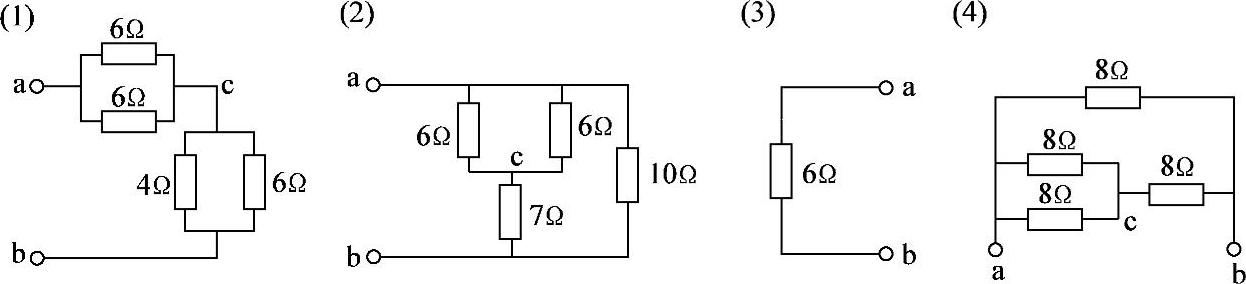
图2-51 习题2.23等效电路

（1）R_ab=[（6∥6）+（4∥6）]Ω=5.4Ω

（2）R_ab=[（6∥6）+7]∥10Ω=5Ω

（3）R_ab=6Ω，其中图2-50c虚线框内的电路被短路。

（4）R_ab=8∥[（8∥8）+8]Ω=4.8Ω

2.24 已知电阻电路如图2-52所示，R₁=R₂=R₃=R₄=R₅=R₆=1Ω，试分别求AB端和CB端等效电阻。

解：R_AB={[（R₃+R₆）∥R₅]+R₂}∥R₄+R₁=1.625Ω

R_CB={[（R₂+R₄）∥R₅]+R₃}∥R₆=0.625Ω

2.25 已知电阻电路如图2-53a所示，R₁=R₂=R₃=R₄=6Ω，试求ab端等效电阻。

解：标出与a、c短接的另两点a、c，改画为观察电阻连接关系较清晰的图2-53b电路。

R_ab=（R₁∥R₂∥R₃）+R₄=[（6∥6∥6）+6]Ω=8Ω

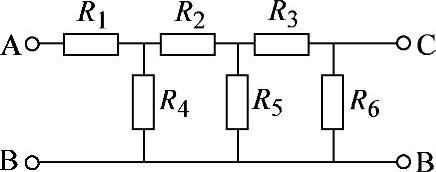
图2-52 习题2.24电路

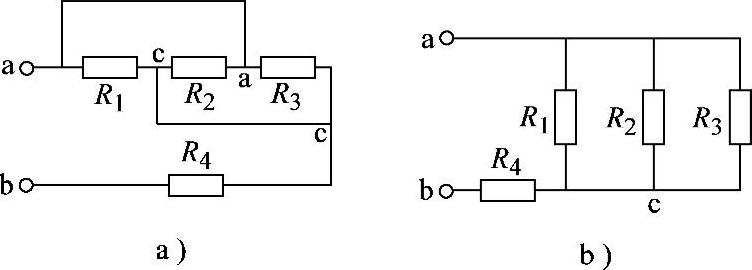
图2-53 习题2.25电路

2.26 已知电阻电路如图2-54a所示，试分别求S开关闭合和断开时ab端等效电阻。

解：（1）S开关闭合时，改画等效电路如图2-54b所示。

R_ab=[（6∥6）+（4∥2）]Ω=4.33Ω

（2）S开关断开时，改画等效电路如图2-54c所示。

R_ab=[（6+4）∥（6+2）]Ω=4.44Ω

2.27 已知分压器电路如图2-55所示，U₁=50V，U₂=15V，U₃=5V，R₁+R₂+R₃=20kΩ，试求分压电阻R₁、R₂和R₃值。

解：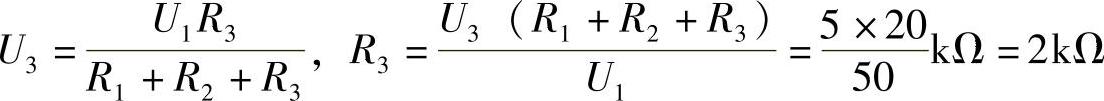

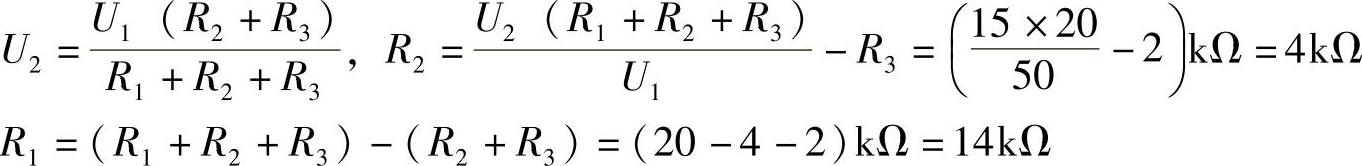
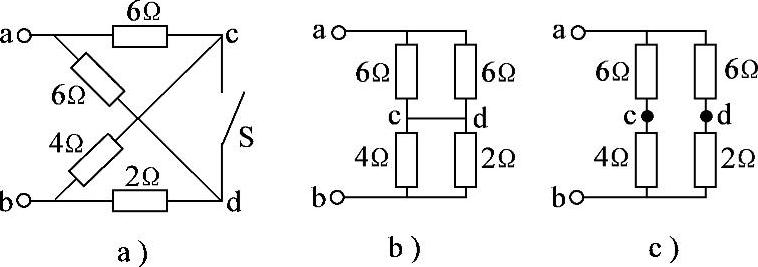
图2-54 习题2.26电路

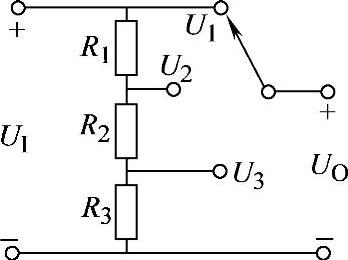
图2-55 习题2.27电路

2.28 已知电路如图2-56所示，试判断下列情况下电压表读数变化：（1）单独合上S₁；（2）单独合上S₂。

解：未合上S₁、S₂时，。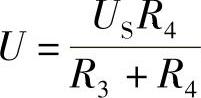

（1）合上S₁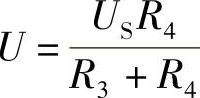：，读数不变；

（2）合上S₂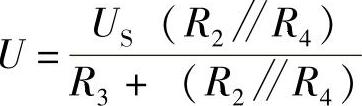，，读数变小。

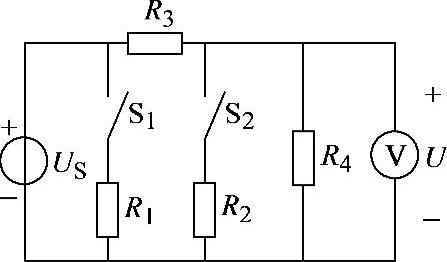
图2-56 习题2.28电路

2.29 已知电路如图2-57所示，R₂为可调电阻，试分析R₂变小时，各电表变化趋势（变大或变小）。

解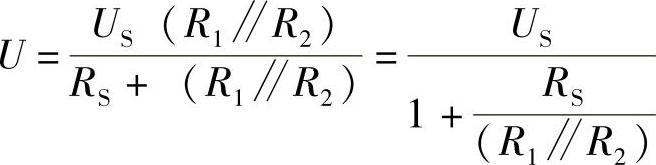：。R₂↓→（R₁∥R₂）↓→↓。

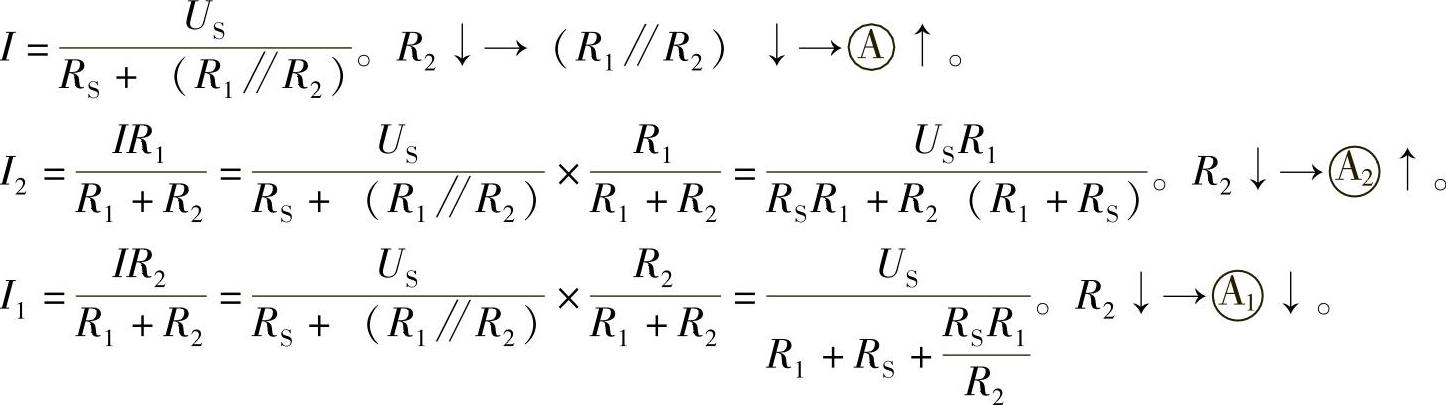
2.30 已知电路如图2-58所示，R₁=R₄=20Ω，R₂=R₃=30Ω，U_ab=25V，求U_S。

解：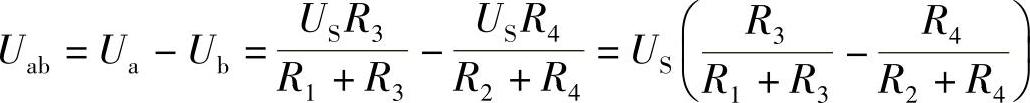

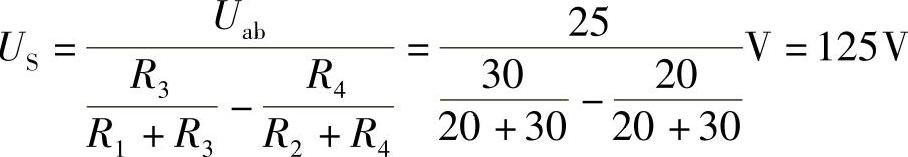
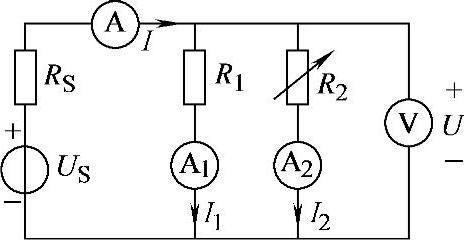
图2-57 习题2.29电路

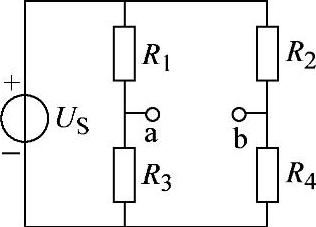
图2-58 习题2.30电路

2.31 已知电路如图2-59a所示，若R=0，则I=-2A；若R→∞，则I=0.333A；若I=0，则R=8Ω。

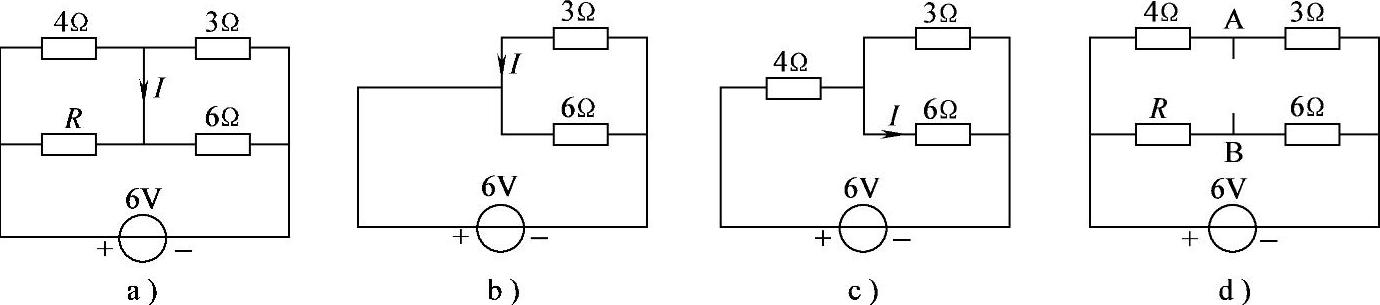
图2-59 习题2.31电路

说明：（1）R=0时，等效电路如图2-59b所示，I为流过3Ω中的电流。

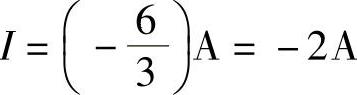
（2）R→∞时，等效电路如图2-59c所示。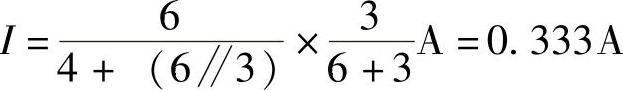

（3）I=0时，等效电路如图2-59d所示，此时UA=UB，。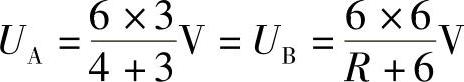

解得R=8Ω

2.32 已知电阻电路如图2-60a所示，R=10Ω，试求R_ab。

解：将图2-60a电路改画为图2-60b电路，再应用△-Y转换为图2-60c所示电路。

则有：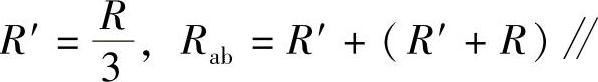

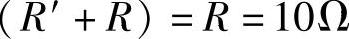
另解：按图2-60b电路，电桥电路平衡，c、d点可短路或开路。

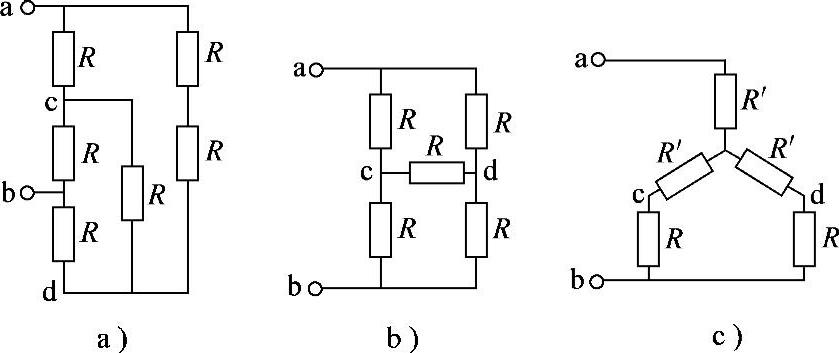
图2-60 习题2.32电路

cd点短路时，R_ab=（R∥R）+（R∥R）=R=10Ω

cd点开路时，R_ab=（R+R）∥（R+R）=R=10Ω

2.33 已知电路如图2-61a所示，R₁=R₅=R₆=40Ω，R₂=R₃=R₄=30Ω，试求ab端入端电阻。

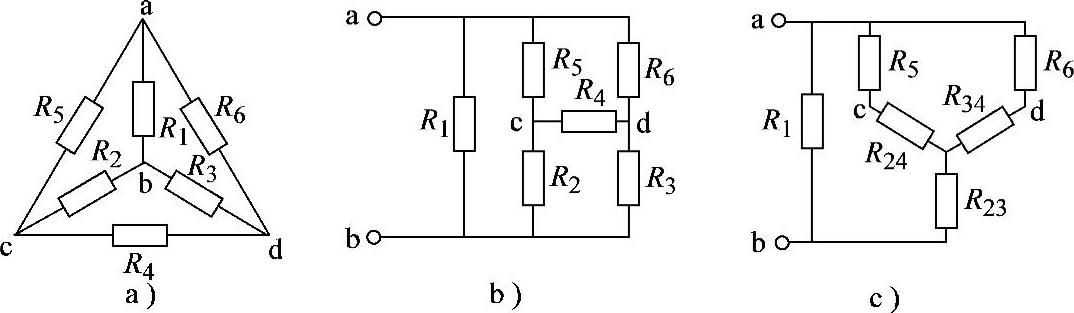
图2-61 习题2.33电路

解：先将图2-61a改画为观察连接关系较清晰的图2-61b电路。再将R₂R₃R₄组成的△形联结转换为Y形联结如图2-61c所示。其中：

R₂₄=R₃₄=R₂₃=R2/3=30/3=10Ω

R_ab=R₁∥{[（R₅+R₂₄）∥（R₆+R₃₄）]+R₂₃}

=40∥{[（40+10）∥（40+10）]+10}Ω=18.67Ω

另解：按2-61b电路，R₅/R₂=R₆/R₃，电桥电路平衡，c、d点可短路或开路。

cd点短路时，R_ab=R₁∥[（R₅∥R₆）+（R₂∥R₃）]=18.67Ω

cd点开路时，R_ab=R₁∥[（R₅+R₂）∥（R₆+R₃）]=18.67Ω

2.34 已知电路如图2-62所示，R₁=8Ω，R₂=4Ω，R₃=6Ω，R₄=3Ω，R₅=8Ω，试求AB端等效电阻。

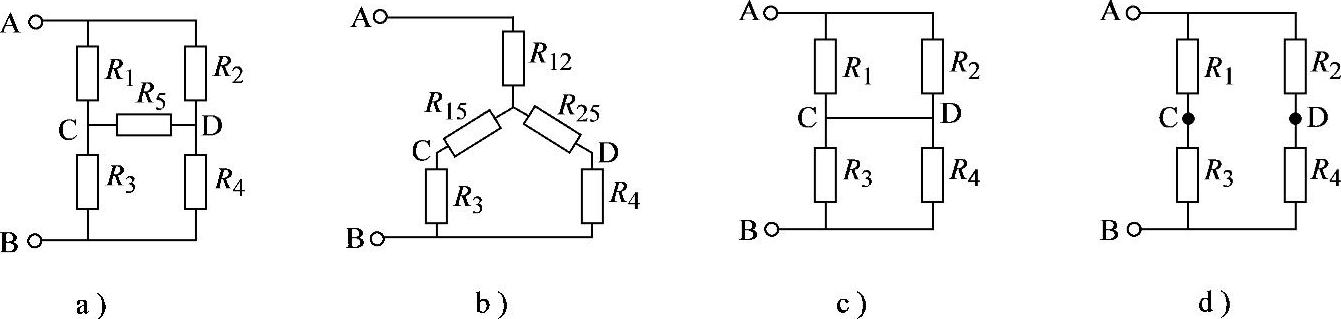
图2-62 习题2.34电路

解：本例有两种求解方法，一种是按Y-△变换求解，另一种是由于本例特殊结构和参数而产生的等电位概念方法求解。

（1）Y-△变换。

按Y-△变换也有多种变换，可以由R₁R₃R₅或R₂R₄R₅组成的Y形联结转换为△形联结，也可以由R₁R₂R₅或R₃R₄R₅组成的△形联结转换为Y形联结。本例分析其中一种，即由R₁R₂R₅组成的△形联结转换为Y形联结，如图2-62b所示。

（2）等电位概念。

由于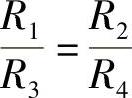，UC=U_D。因此，可用短路线代替，如图2-62c所示。

R_AB=（R₁∥R₂）+（R₃∥R₄）=[（8∥4）+（6∥3）]Ω=4.67Ω

又由于U_C=U_D，R₅中电流为0，因此，相当于开路，如图2-62d所示。

R_AB=（R₁+R₃）∥（R₂+R₄）=[（8+6）∥（4+3）]Ω=4.67Ω

需要指出的是，桥式电路应用等电位概念必须满足条件。

2.35 已知电路如图2-63a所示，R₁=R₂=R₃=6Ω，R₄=R₅=3Ω，试求ab端等效电阻。

解：本题有多种解法，现推出两种。

方法（1）：将R₁、R₂、R₅组成的△形联结电路转换为R₁₂、R₁₅、R₂₅组成的Y形联结电路，如图2-63b所示。

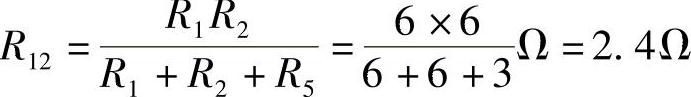
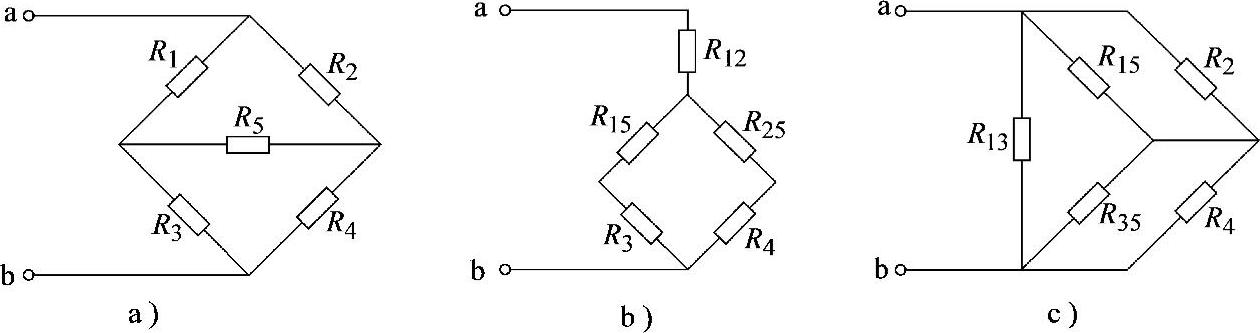
图2-63 习题2.35电路

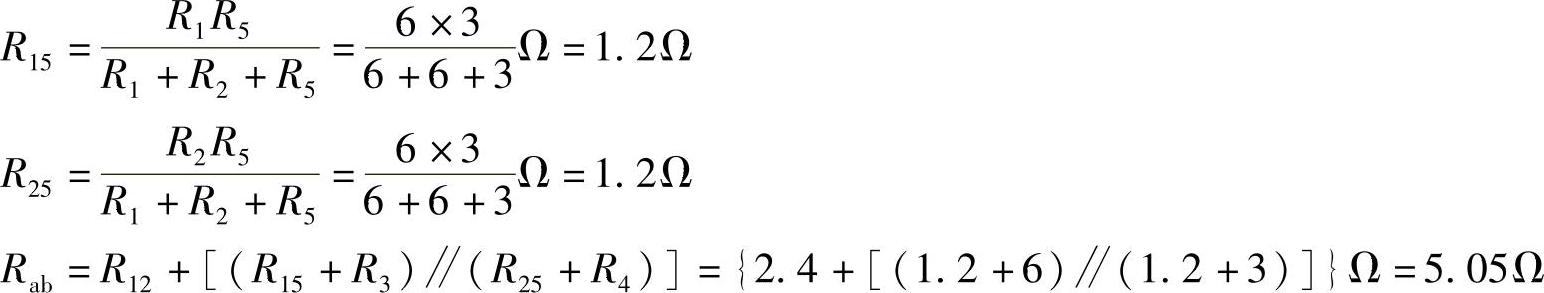
方法（2）：将R₁、R₃、R₅组成的Y形联结电路转换为R₁₃、R₁₅、R₃₅组成的△形联结电路，如图2-63c所示。

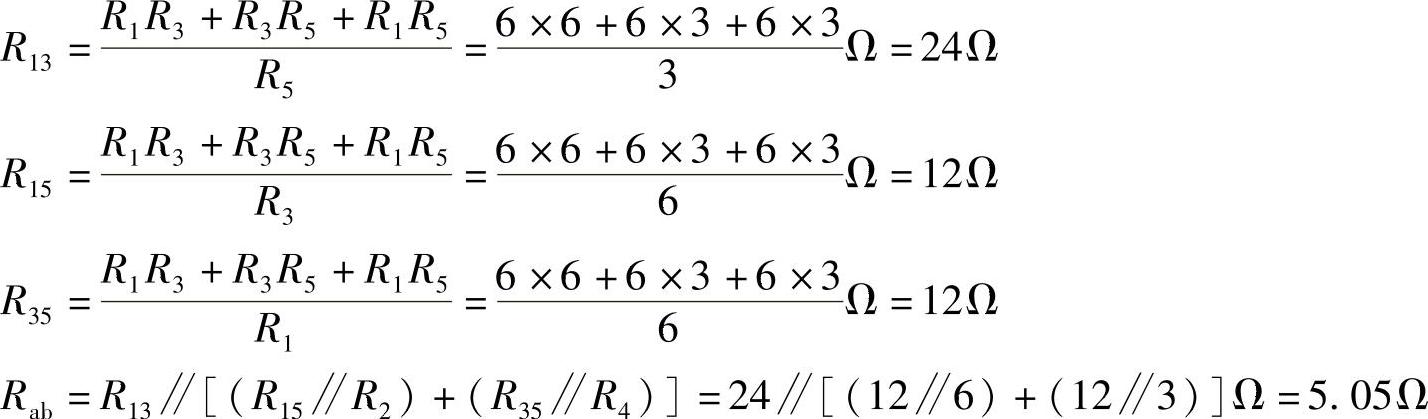
2.36 试化简并分析图2-64所示电路。

解：电源等效变换过程如图2-64所示。

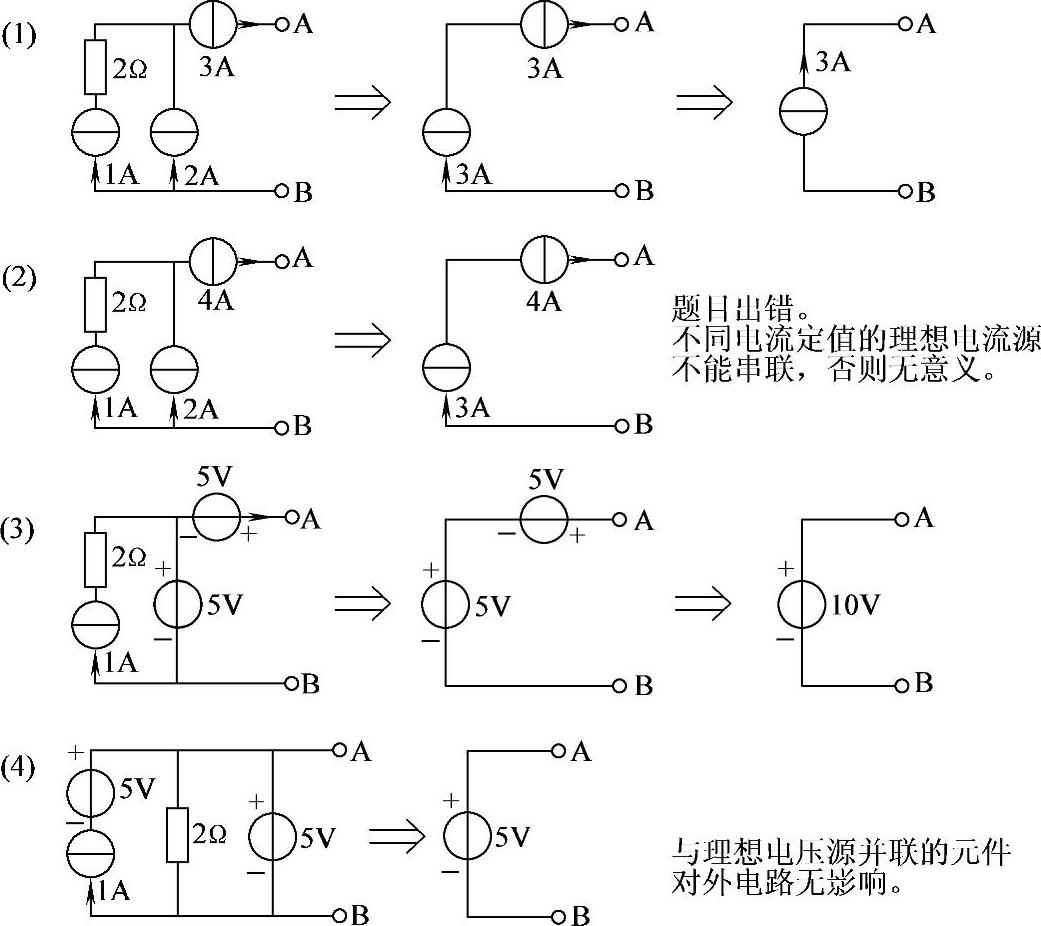
图2-64 习题2.36电路

2.37 利用电源等效变换化简图2-65所示电路。

解：电源等效变换过程如图2-65所示。

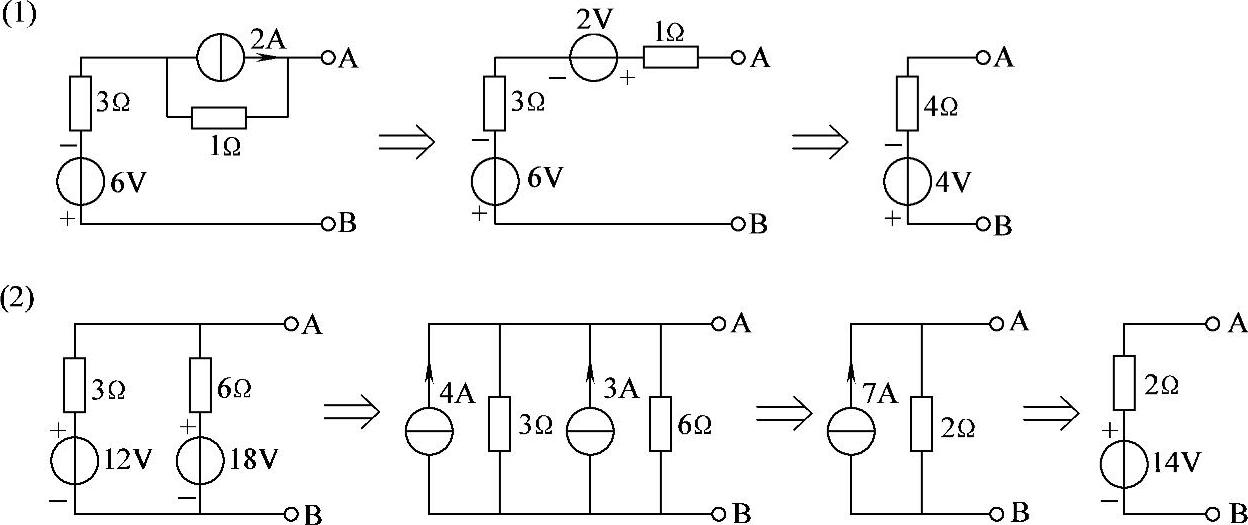
图2-65 习题2.37电路

2.38 已知电路如图2-66a所示，R₁=R₂=100Ω，R₃=50Ω，U_S1=100V，I_S2=0.5A，试利用电源等效变换求电阻R₃中的电流I。

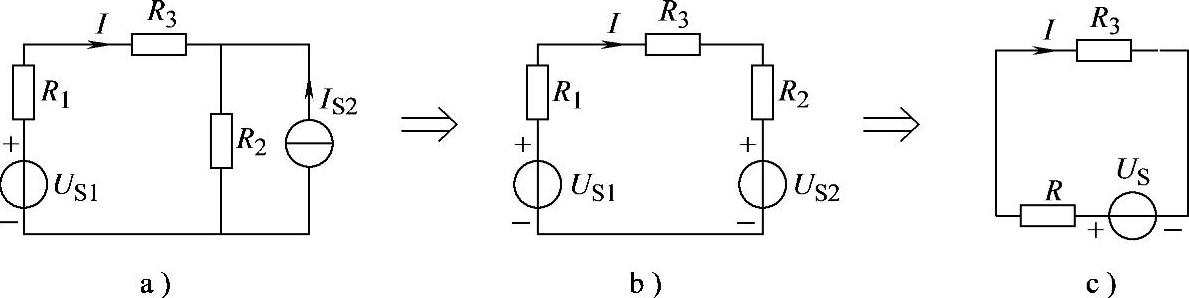
图2-66 习题2.38电路

解：将图2-66a所示电路依次等效变换图2-66b、c所示电路。其中：

U_S2=I_S2R₂=0.5×100V=50V

R=R₁+R₂=（100+100）Ω=200Ω

U_S=U_S1-U_S2=（100-50）V=50V

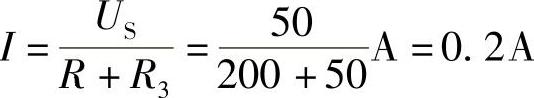
2.39 已知电路如图2-67a所示，R₁=R₂=R₃=6Ω，R₄=R₅=3Ω，U_S=12V，I_S=3A，试利用电源等效变换求解I₅。

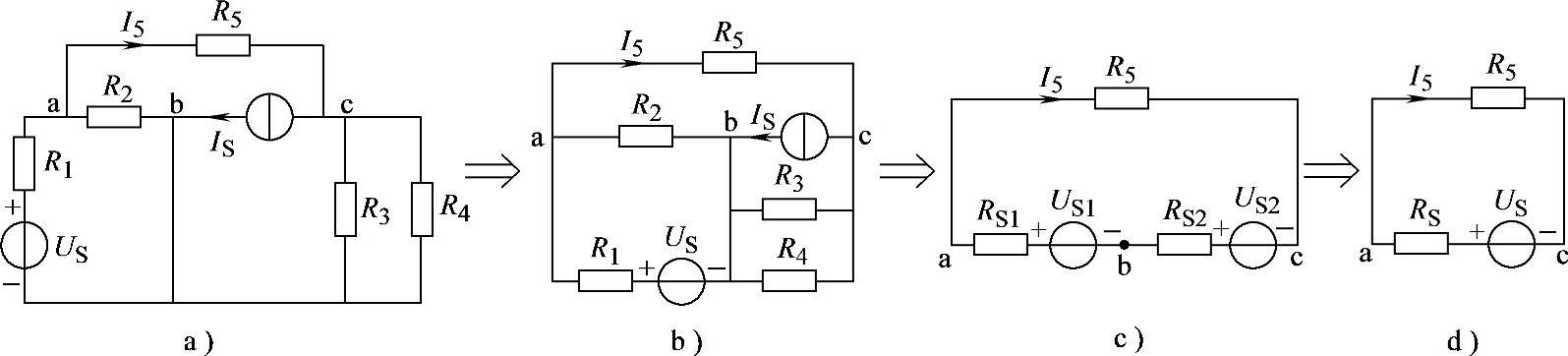
图2-67 习题2.39电路

解：（1）将图2-67a电路改画为容易看清连接关系的电路如图2-67b所示。

（2）ab端和bc端分别等效变换如图2-67c所示。

R_S1=R₁∥R₂=6∥6=3Ω，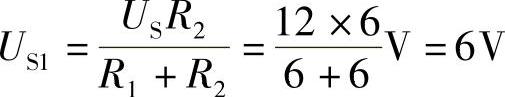

R_S2=R₃∥R₄=6∥3=2Ω，U_S2=I_SR_S2=3×2V=6V

（3）ab端电压源与bc端电压源串联合并，如图2-67d所示。

U_S=U_S1+U_S2=6+6=12V，R_S=R_S1+R_S2=（3+2）Ω=5Ω

（4）计算I₅：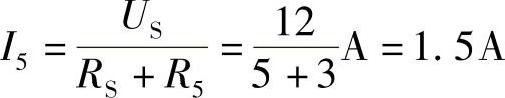

2.40 已知电路如图2-68所示，试按图中I_a、I_b、I_c绕行方向列出网孔电流方程。

解：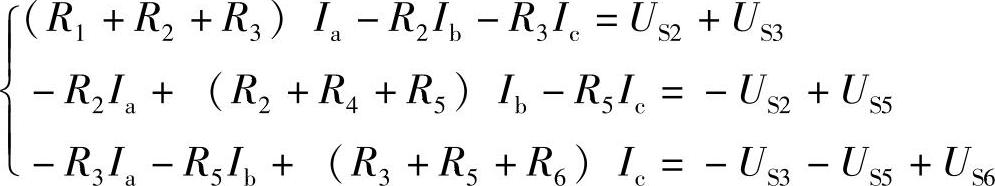

2.41 已知电路如图2-69a所示，试列出网孔电流方程。

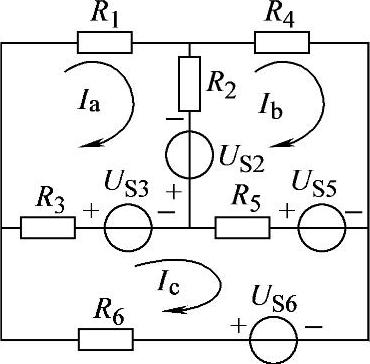
图2-68 习题2.40电路

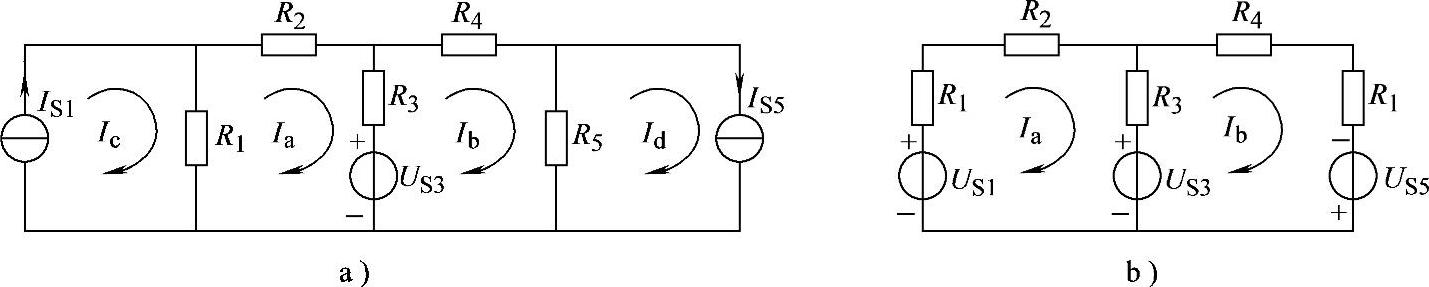
图2-69 习题2.41电路

解：标出网孔电流I_a、I_b、I_c和I_d，列出网孔电流方程。

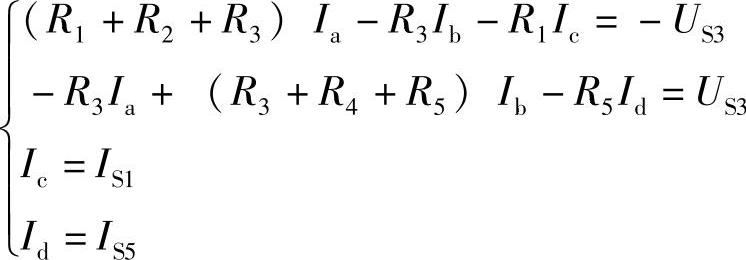
也可先将电路中电流源转换为电压源，如图2-69b所示，然后列出网孔电流方程。

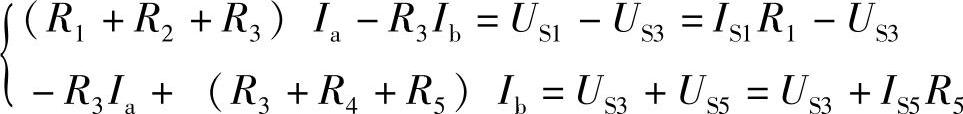
2.42 已知电路如图2-70所示，U_S1=20V，U_S2=10V，U_S3=13V，R₁=R₃=5Ω，R₂=4Ω，试用网孔电流法求解各支路电流I₁、I₂和I₃。

解：先标出网孔电流I_a、I_b参考方向如图2-70所示，则有：

代入数据得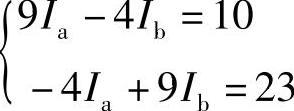

联立求解得：I_a=2.8A，I_b=3.8A

I₁=I_a=2.8A

I₂=I_a-I_b=（2.8-3.8）A=-1A

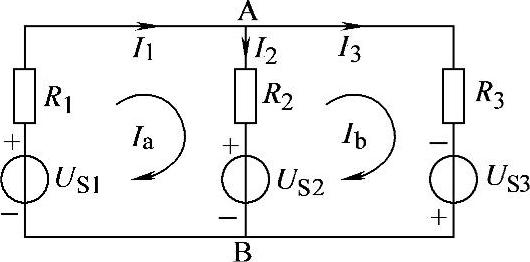
图2-70 习题2.42电路

I₃=I_b=3.8A

2.43 已知电路如图2-71所示，试以O为参考节点，列出A、B节点电压方程。

解：列出节点电压方程时，与理想电流源I_S4串联的电阻R₄对I_S4支路以外的电路不起作用，因此此节点电压方程中不应列入。

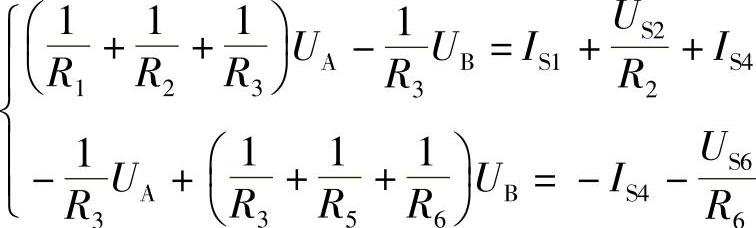
2.44 已知电路如图2-72所示，U_S1=6V，U_S3=4V，U_S5=11V，R₁=2Ω，R₂=R₃=R₄=R₅=4Ω，试用节点电压法求解各支路电流I₁～I₅。

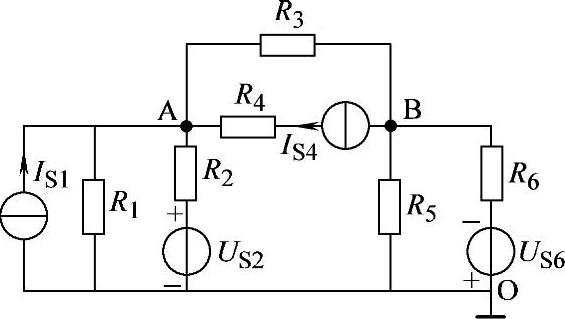
图2-71 习题2.43电路

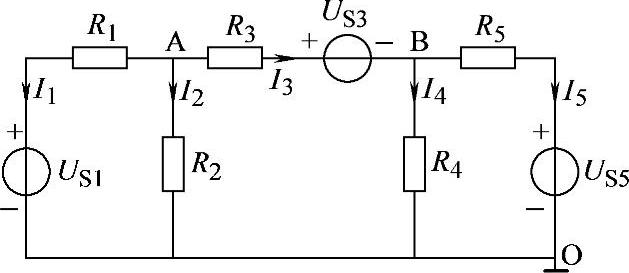
图2-72 习题2.44电路

解：以O点为参考节点，列出A、B两节点的节点电压方程：

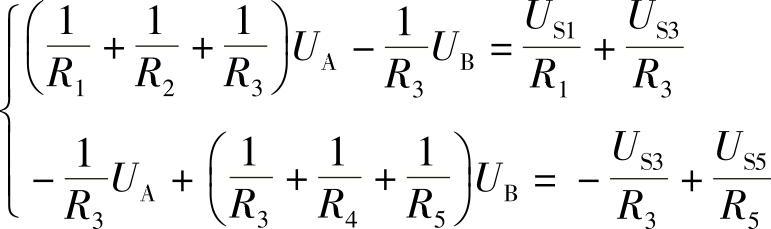
代入数据得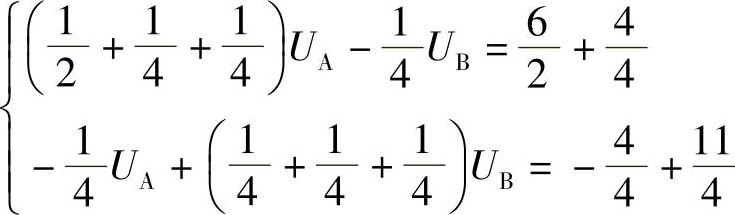即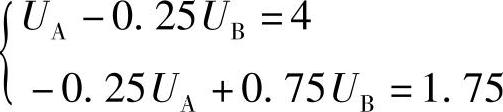

解得 U_A=5V，U_B=4V

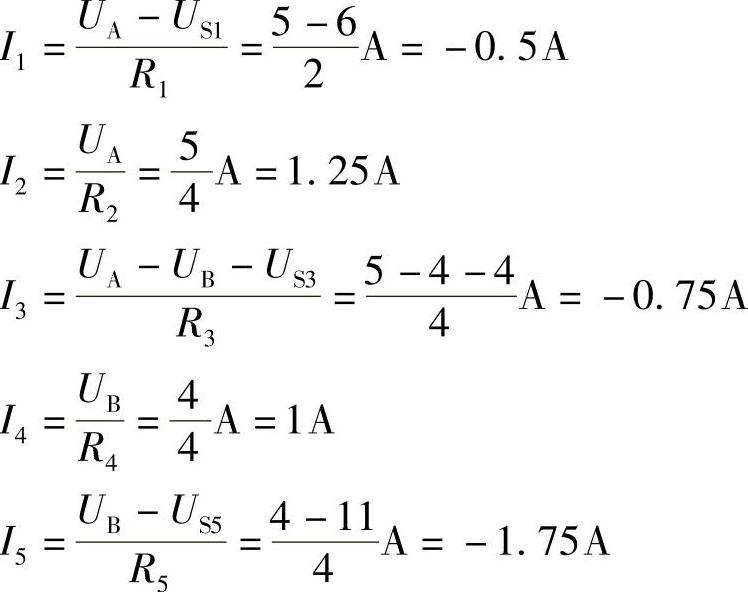
2.45 已知电路如图2-73所示，R₁=R₂=5Ω，R₃=R₄=10Ω，R₅=15Ω，U_S1=15V，U_S5=65V，试用节点电压法求解各支路电流I₁～I₅。

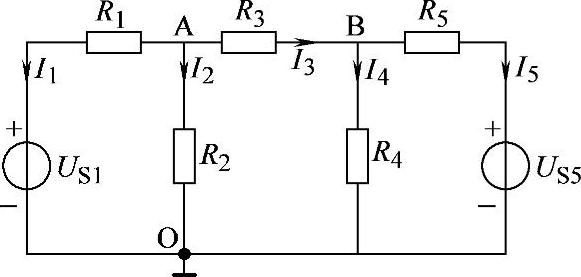
图2-73 习题2.45电路

解：以O点为参考节点，列出A、B节点电压方程：

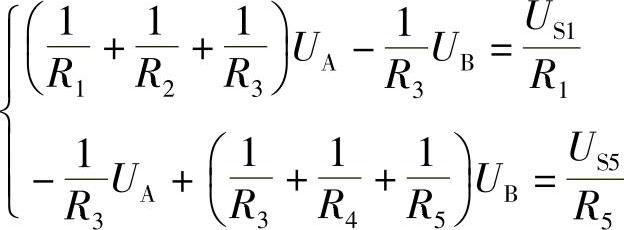代入数据得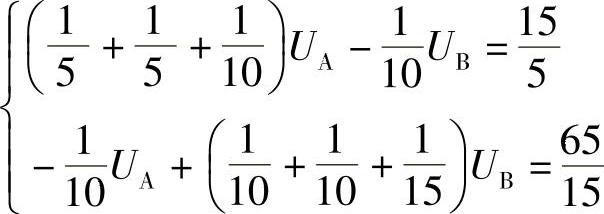

即：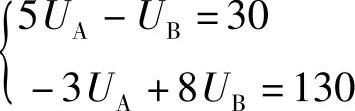

解得：U_A=10V，U_B=20V

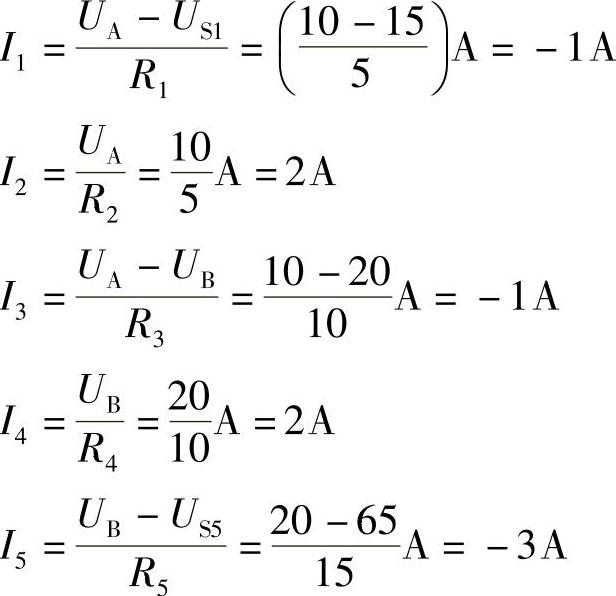
2.46 已知电路如图2-74所示，R₁=R₂=R₃=R₄=R₅=R₆=10Ω，I_S3=2A，U_S4=20V，U_S5=50V，试用弥尔曼定理求U_A。

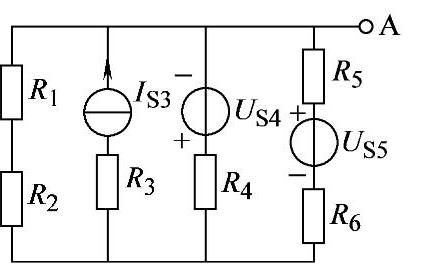
图2-74 习题2.46电路

解：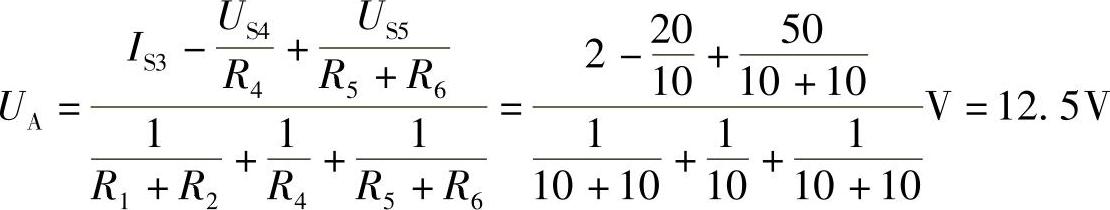

2.47 电路和元件参数同图2-70和题2.42，试用弥尔曼定理求支路电流I₁、I₂和I₃。

解：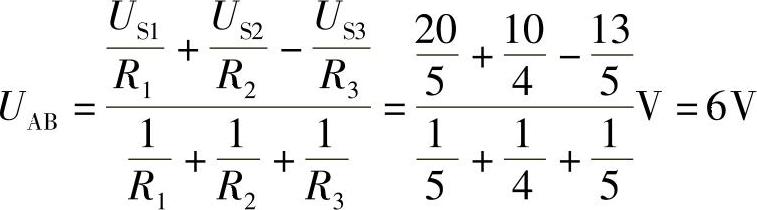

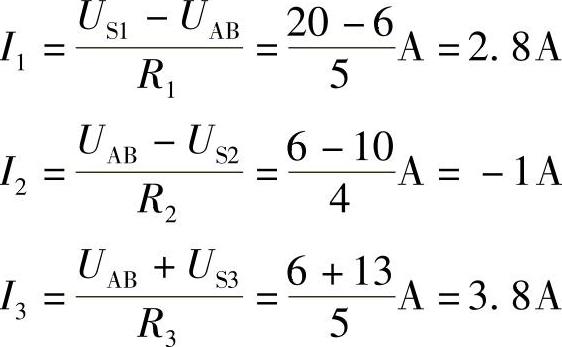
与题2.42要求用网孔电流法求解相比，用弥尔曼定理求解的方法要简洁方便得多。因此，凡两个节点的电路，一般宜用弥尔曼定理求解。

2.48 已知电路如图2-75a所示，U_S=24V，R₁=200Ω，R₂=100Ω，I_S=1.5A，试用叠加定理求解电流I。

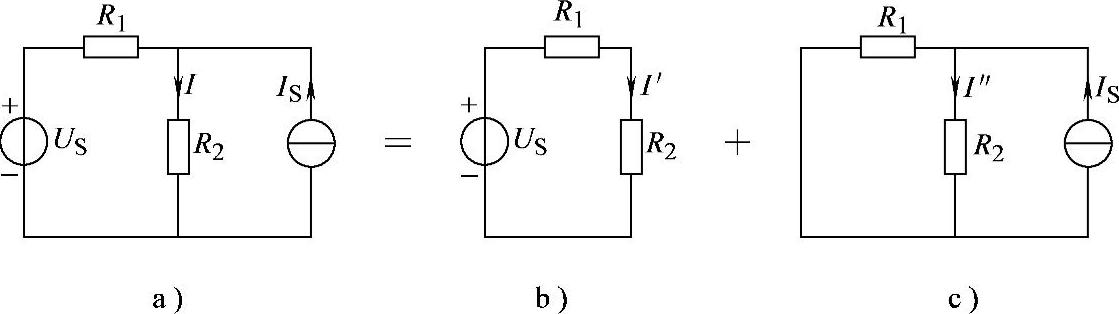
图2-75 习题2.48电路

解：通过叠加定理，求解电路如图2-75b、c所示。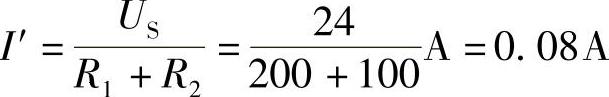

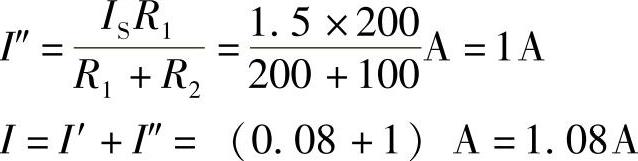
2.49 已知电路如图2-76所示，R₁=10Ω、R₂=50Ω、R₃=40Ω、U_S1=28V、U_S2=5V，试分别用支路电流法、网孔电流法、叠加定理和弥尔曼定理求解支路电流I₁、I₂和I₃。

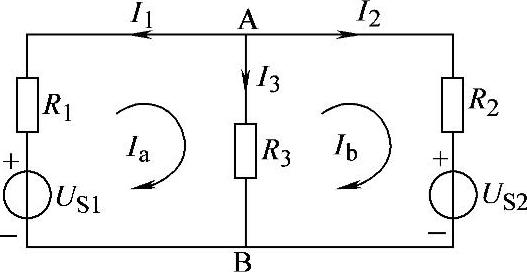
图2-76 习题2.49电路

解：（1）支路电流法。

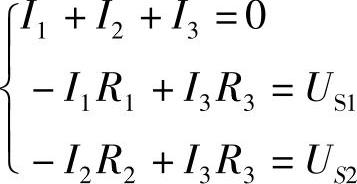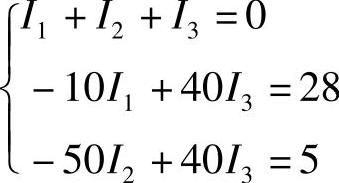代入数据得联立求解得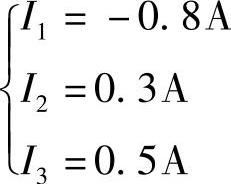

（2）网孔电流法。

画出网孔电流I_a、I_b及其绕行方向。

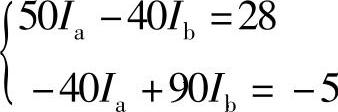代入数据得联立求解得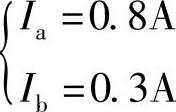

因此：I₁=-I_a=-0.8A

I₂=I_b=0.3A

I₃=I_a-I_b=（0.8-0.3）A=0.5A

（3）弥尔曼定理。

标出节点A、B，则有：

（4）叠加定理。

画出叠加定理求解电路如图2-77所示。

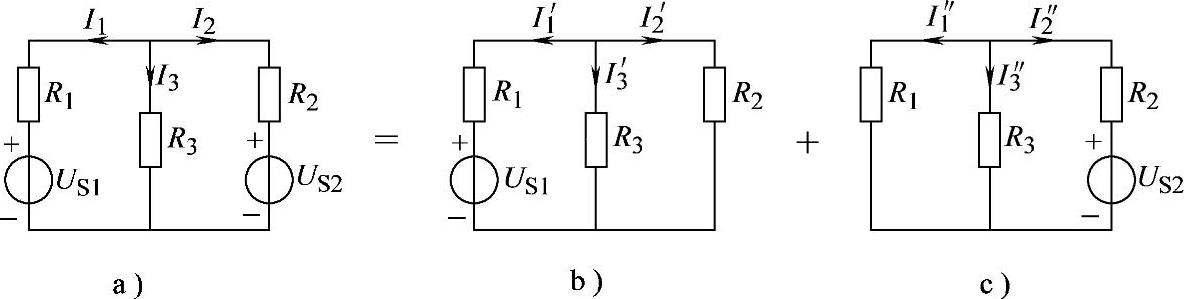
图2-77 习题2.49叠加定理求解电路

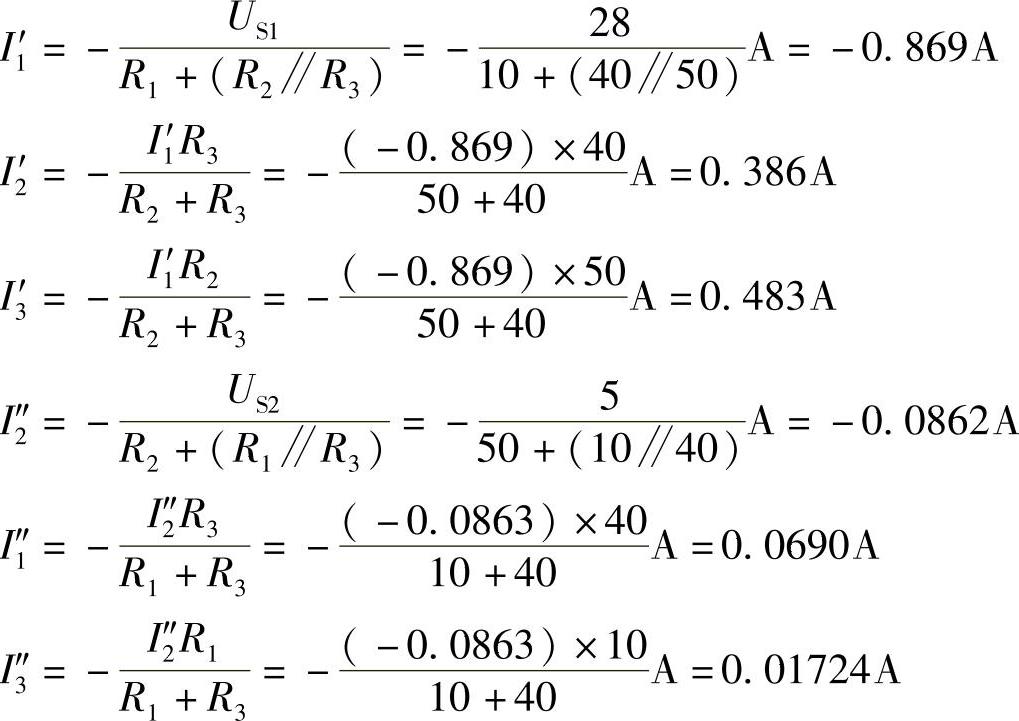
I₁=I₁′+I″₁=[（-0.869）+（-0.069）]A=-0.8A

I₂=I₂′+I₂″=[0.386+（-0.0862）]A=0.3A

I₃=I₃′+I₃″=（0.483+0.01724）A=0.5A

2.50 已知电路如图2-78a所示，R₁=R₂=10Ω，R₃=20Ω，U_S1=3V，I_S2=1.2A，试用叠加定理求支路电路I₁、I₃，并求各元件功率。

解：画出叠加定理求解电路如图2-78b、c所示。

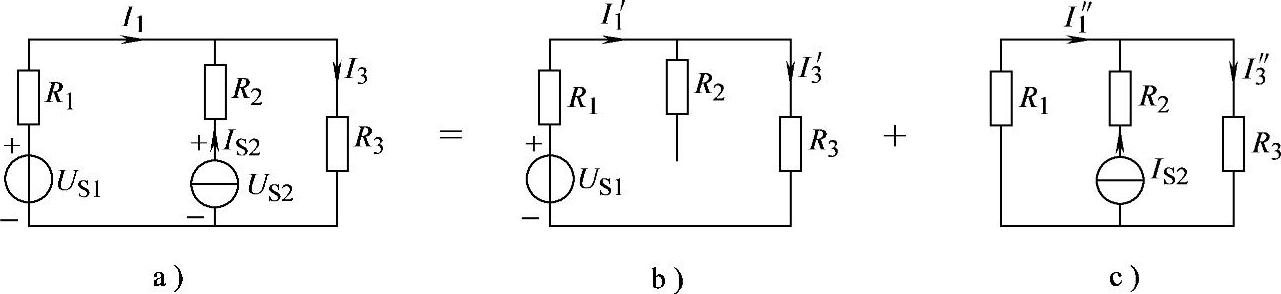
图2-78 习题2.50电路

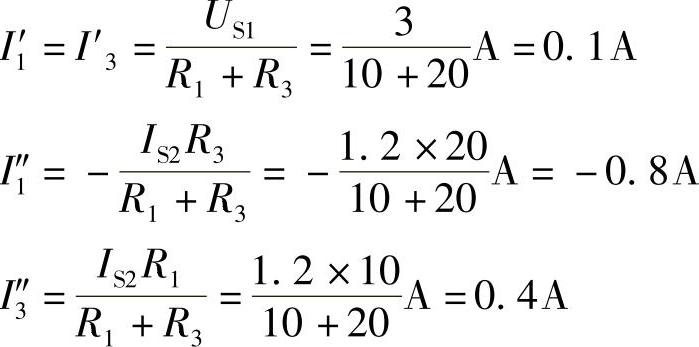
I₁=I₁′+I″₁=[0.1+（-0.8）]A=-0.7A

I₃=I₃′+I₃″=（0.1+0.4）A=0.5A

P_US1=-U_S1I₁=[-3×（-0.7）]W=2.1W（吸收功率）

P_R1=I²₁R₁=（-0.7）2×10W=4.9W（吸收功率）

P_R2=I²_S2R₂=（1.2）2×10W=14.4W（吸收功率）

P_R3=I²₃R₃=（0.5）2×20W=5W（吸收功率）

P_IS2=-I_S2U_S2=-I_S2（I_S2R₂+I₃R₃）

=[-1.2×（1.2×10+0.5×20）]W=-26.4W（发出功率）

P_IS2=P_US1+P_R1+P_R2+P_R3，功率平衡。

2.51 已知电路如图2-79a所示，I_S1=2A，I_S2=4A，R=2Ω，试用叠加定理求各支路电流I₁、I₂和I₃。

图2-79 习题2.51电路

解：画出叠加定理求解电路如图2-79b、c所示。

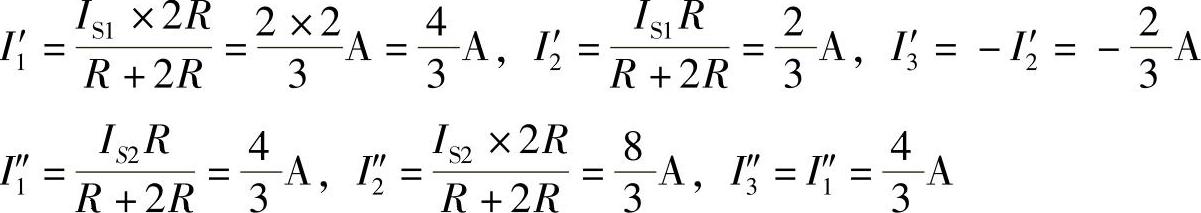
因此，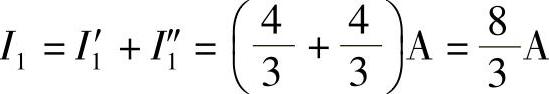

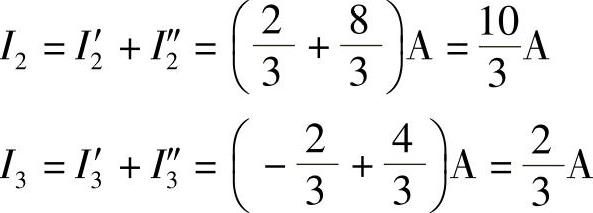(www.xing528.com)

2.52 已知电路如图2-80a所示，与图2-79a相比，电路中多了一个电压源U_S3=6V，其余部分均相同，试再求各支路电流。

图2-80 习题2.52电路

解：本题可利用上题电路解答，将上题解答作为I₁′、I₂′、I₃′，将U_S3单独作用作为I″₁、I″₂、I″₃，画出叠加定理求解电路如图2-80b、c所示。

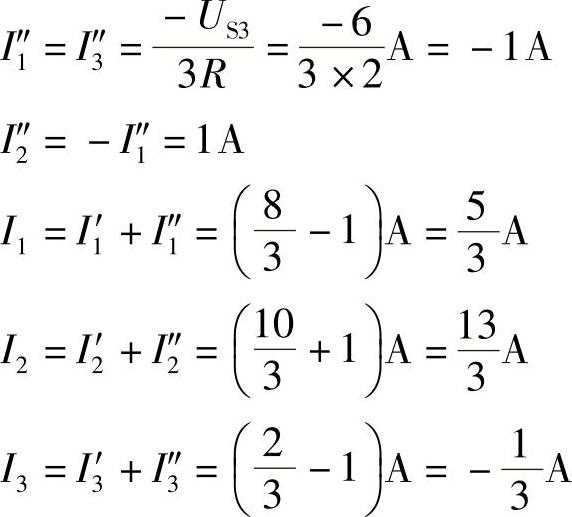
2.53 已知电路如图2-81a所示，试用叠加定理求解6Ω电阻中电流I。

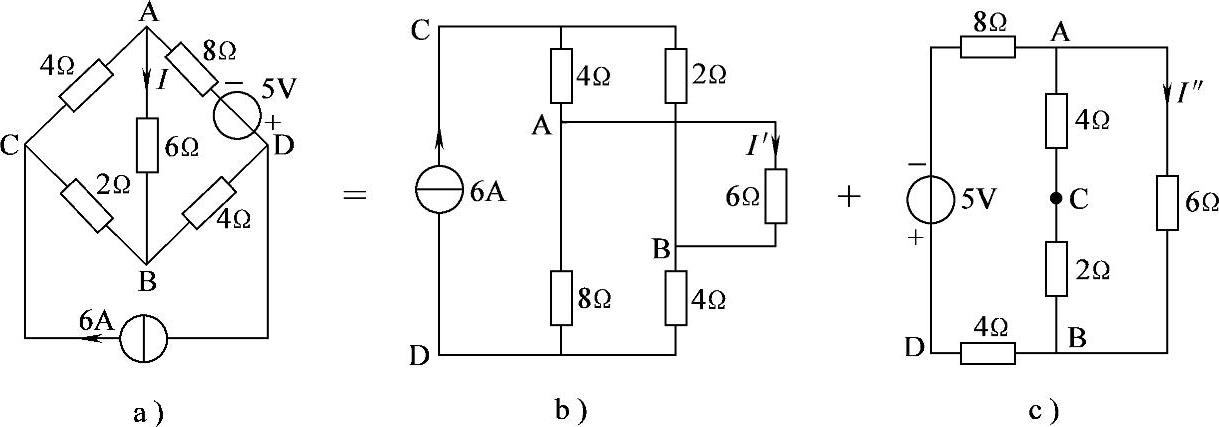
图2-81 习题2.53电路

解：画出叠加定理求解电路如图2-81b、c所示。

图2-81b中，4/8=2/4，电桥平衡，A、B等电位，I′₁=0

图2-81c中，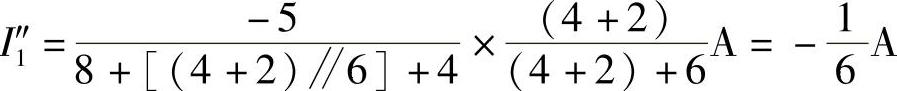

因此，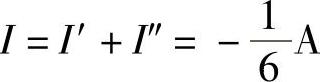

2.54 已知电路如图2-82a所示，试用叠加定理求U_AB。

解：画出叠加定理求解电路如图2-82b、c所示。

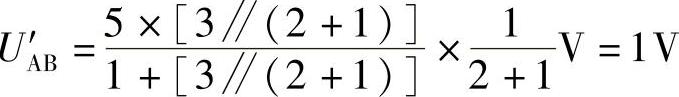（先求3Ω上分压，再求1Ω上分压）

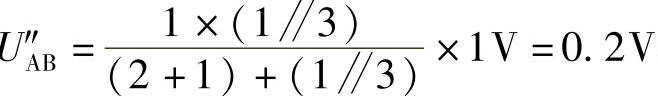（分流后求1Ω上电压）

U_AB=U_A′_B+U″_AB=（1+0.2）V=1.2V

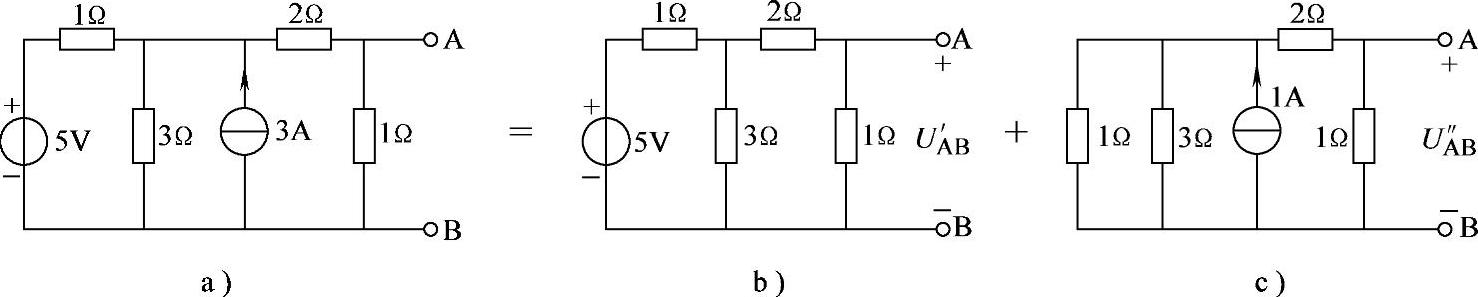
图2-82 习题2.54电路

2.55 已知电路如图2-83所示，U_S2=4V，U_S3=6V，S开关在位置1时，毫安表读数I=40mA；S开关在位置2时，I=-60mA，求S开关在位置3时毫安表读数。

解：（1）S在位置1时，U_S1单独作用，I′=40mA

（2）S在位置2时，U_S1与U_S2共同作用，I=-60mA，设U_S2单独作用时为I″，则

I=I′+I″，I″=I-I′=[（-60）-40]mA=-100mA，因此，U_S2单独作用时I″=-100mA。

（3）S在位置3时，U_S1与U_S3共同作用，设U_S3单独作用时为I″′，与U_S2单独作用相比，可根据齐性定理推出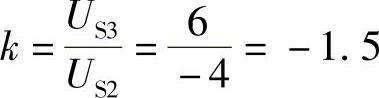，，I″′=kI″=（-1.5）×（-100）mA=150mA

因此，U_S1与U_S3共同作用时，I=I′+I″′=（40+150）mA=190mA

2.56 试用齐性定理求解图2-84所示电路中各支路电流I₁～I₅。已知U_S=100V，R₁=R₃=R₅=4Ω，R₂=R₄=R₆=10Ω。

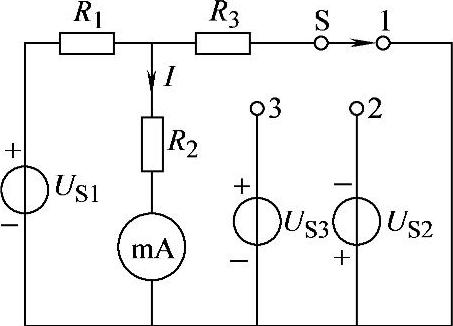
图2-83 习题2.55电路

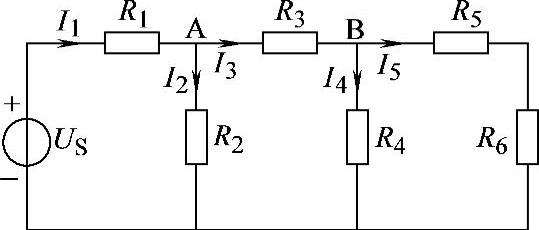
图2-84 习题2.56电路

解：设I₅′=1A，则U_B′=I₅′（R₅+R₆）=1×（4+10）V=14V

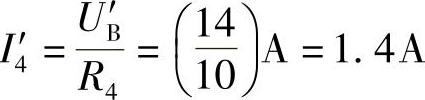
I₃′=I₄′+I₅′=（1.4+1）A=2.4A

U_A′=I₃′R₃+U_B′=（2.4×4+14）V=23.6V

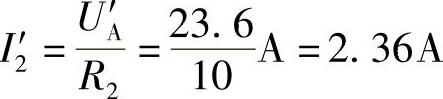
I₁′=I₂′+I₃′=（2.36+2.4）A=4.76A

U_S′=I₁′R₁+U_A′=（4.76×4+23.6）V=42.64V

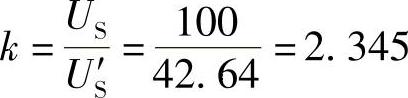
因此，I₁=kI₁′=（2.345×4.76）A=11.16A

I₂=kI₂′=2.345×2.36A=5.534A

I₃=kI₃′=2.345×2.4A=5.628A

I₄=kI₄′=2.345×1.4A=3.283A

I₅=kI₅′=2.345×1A=2.345A

2.57 试求图2-85中各电路的AB端戴维南等效电路。

2.58 已知电路如图2-86所示，试求其AB端戴维南等效电路。

说明：其中图2-86（4）中，与理想电流源串联的电阻（2Ω）对外电路不起作用，与理想电压源并联的电阻（3Ω）对外电路不起作用，因此对外电路来讲可将其删除。

2.59 已知电路如图2-87a所示，试求ab端戴维南等效电路。

解：首先将电路改画成容易看清连接关系的电路，如图2-87b所示，然后依次等效变换，如图2-87c、d所示。

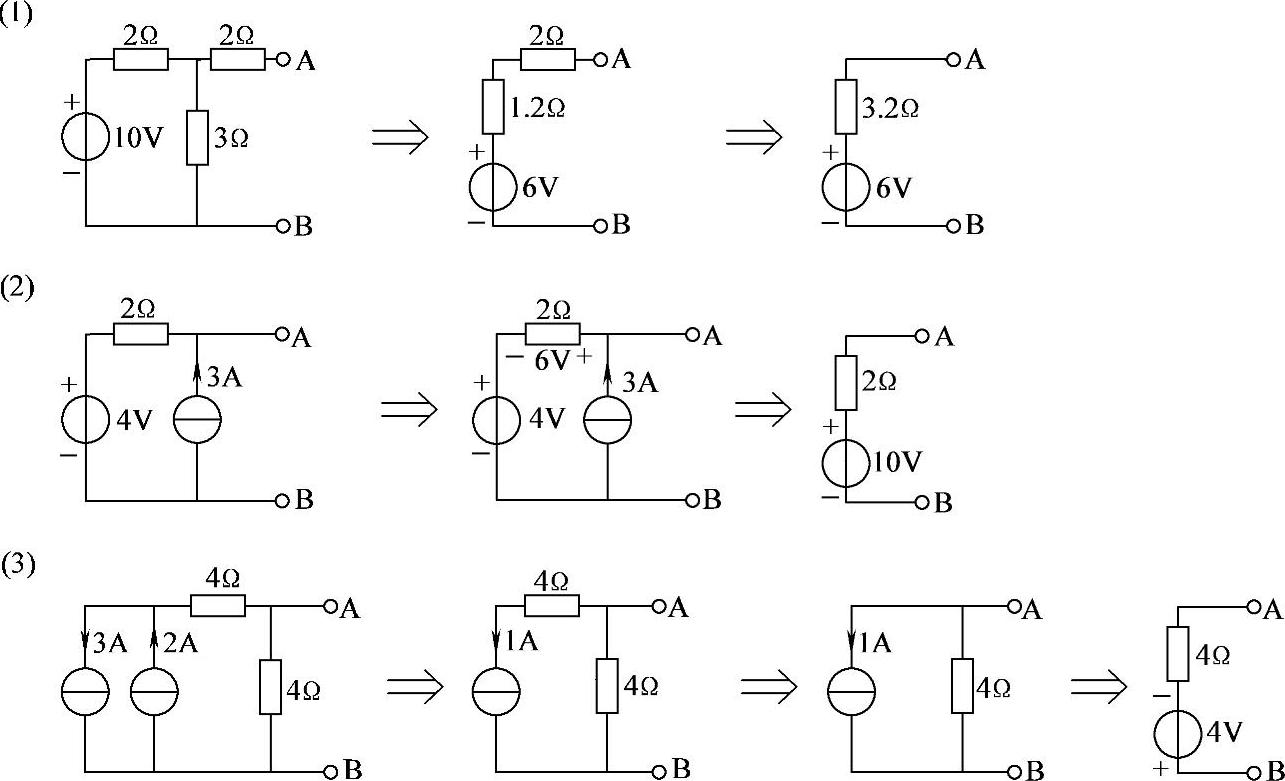
图2-85 习题2.57电路

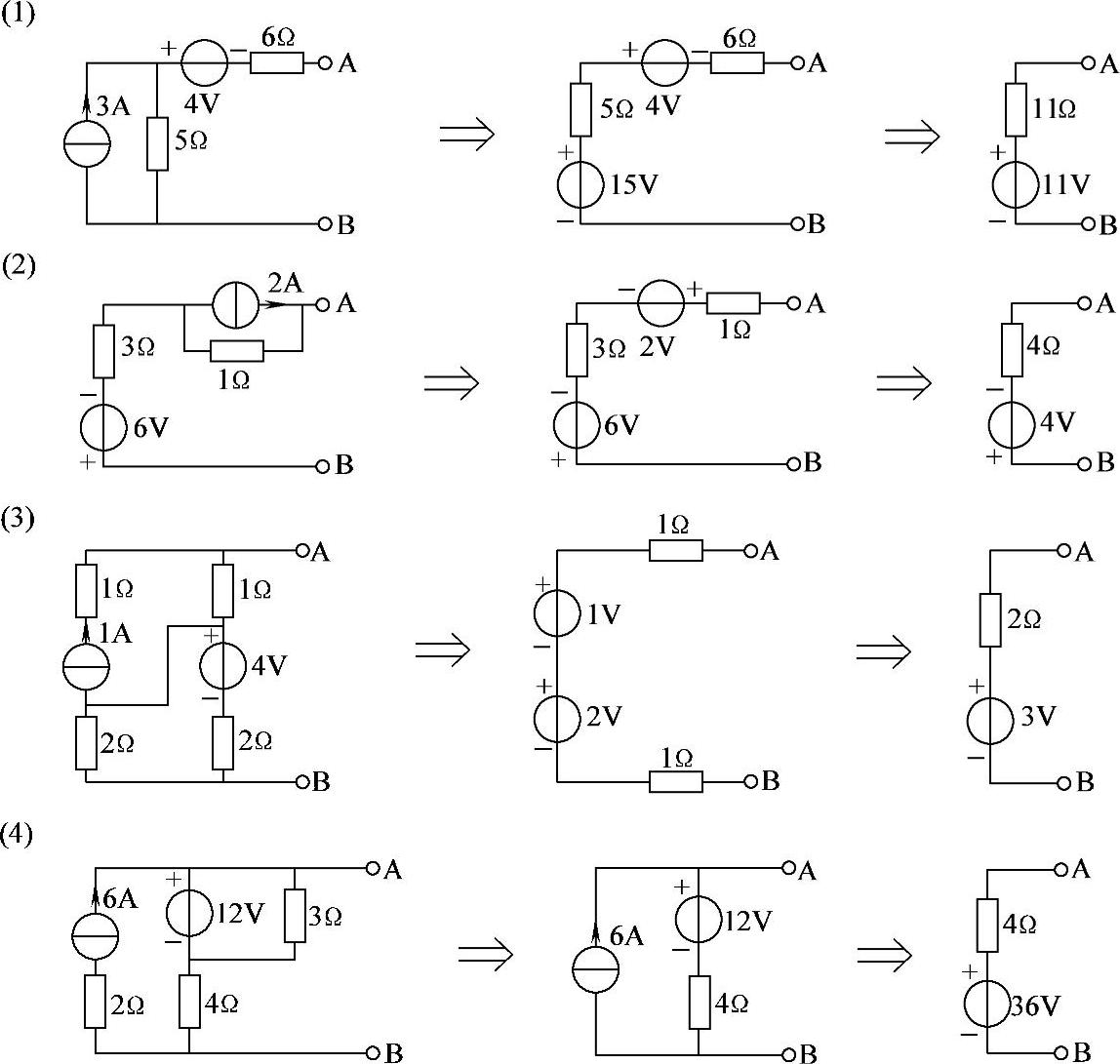
图2-86 习题2.58电路

2.60 已知电路如图2-88a所示，R₁=1Ω，R₂=4Ω，R₃=3Ω，R₄=4Ω，U_S=12V，试求AB端戴维南等效电路。

解：有两种解法。

方法（1）：将R₁R₂R₃组成的△形联结电路转换为Y形联结电路，如图2-88b所示。其中：

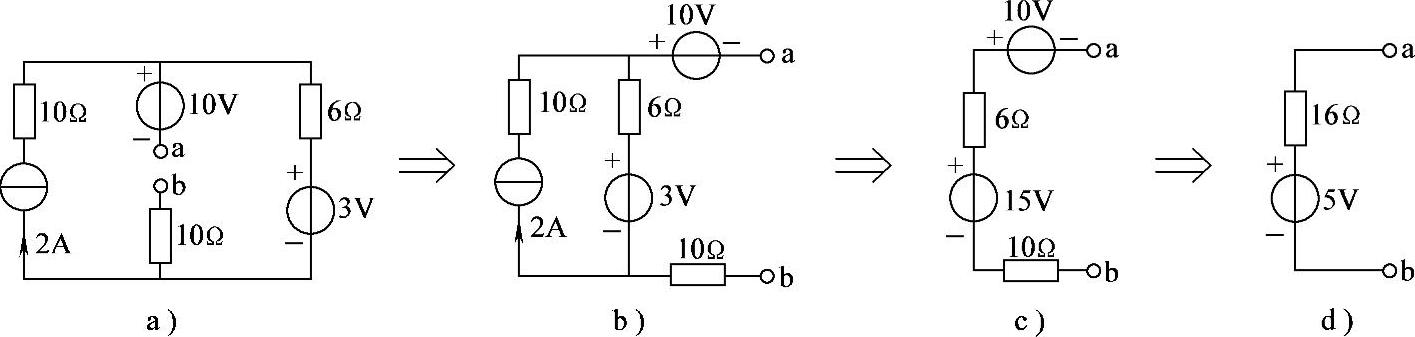
图2-87 习题2.59电路

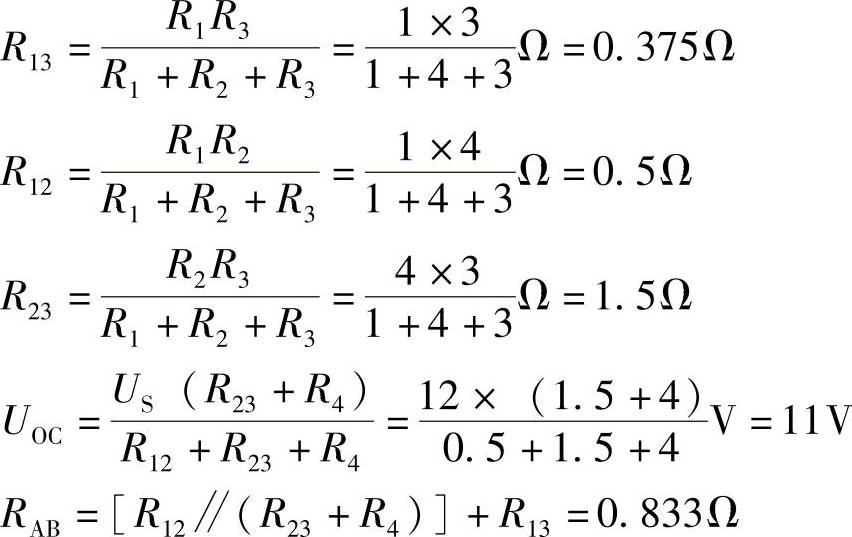
据此，画出戴维南等效电路如图2-88c所示。

方法（2）：将图2-88a电路改画为图2-88d电路，则有：

图2-88 习题2.60电路

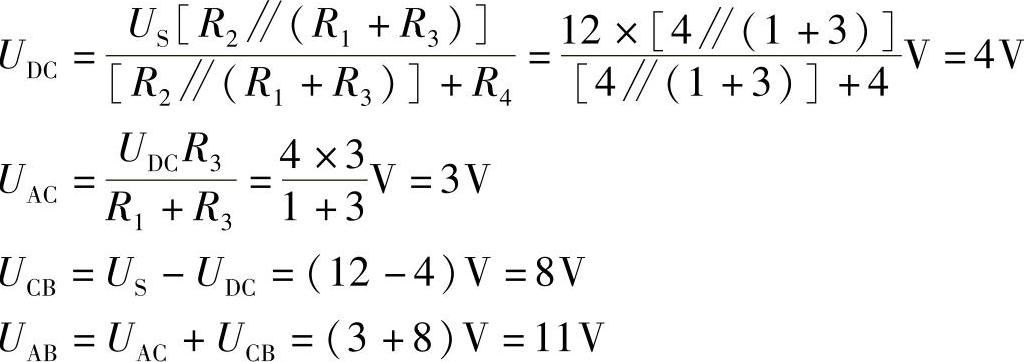
求R_AB等效电路如图2-88e所示。

R_AB=R₁∥[R₃+（R₂∥R₄）]=1∥[3+（4∥4）]Ω=0.833Ω

相比之下，方法（2）更清晰简便些。

2.61 已知电路如图2-89a所示，

U_S=8V，R₁=R₂=R₃=2Ω，R₄=1Ω，

试用戴维南定理求解R₄中电流I。

解：将电路依次等效为图2-89b、c所示电路。

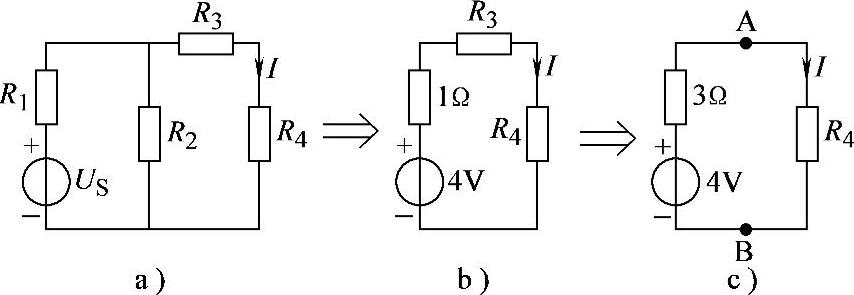
图2-89 习题2.61电路

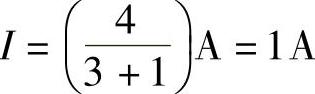
2.62 已知U_S1=24V，U_S2=-6V，R₁=12Ω，R₂=6Ω，R₃=4Ω，试用戴维南定理求图2-90a所示电路的电流I。

解：将图2-90a电路等效变换为图2-90b电路，其中：

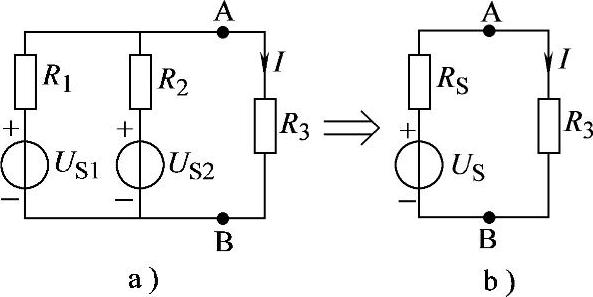
图2-90 习题2.62电路

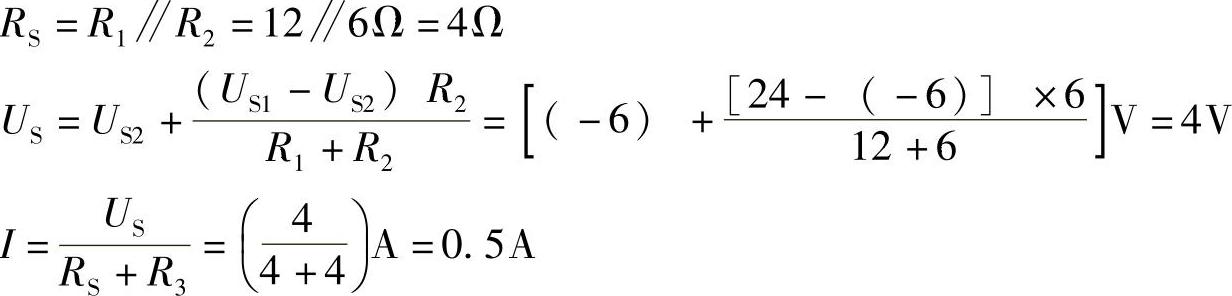
2.63 已知电路如图2-91a所示，U_S=8V，I_S=2A，R₁=R₂=R₃=2Ω，试用戴维南定理求解I₃。

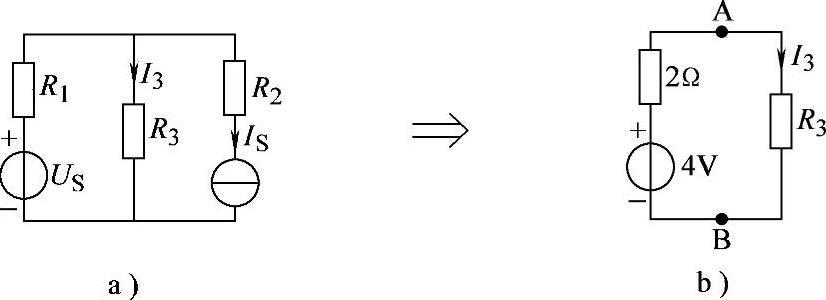
图2-91 习题2.63电路

解：将由R₁、U_S、R₂和I_S组成的部分电路戴维南等效变换为图2-91b所示电路。

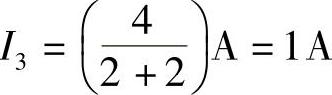
2.64 已知电路如图2-92a所示，U_S=20V，I_S=1A，R₁=R₂=10Ω，R₃=R₄=5Ω，试用戴维南定理求解电流I。

图2-92 习题2.64电路

解：按电源等效变换分别得出图2-92b、c电路：

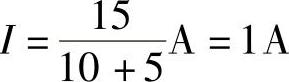
2.65 已知电路如图2-93a所示，U_S=48V，R₁=2Ω，R₂=R₄=3Ω，R₃=6Ω，R_L=5Ω，试用戴维南定理求解I_O。

解：将图2-93a画成图2-93b形式，看起来更清晰些，求出开路电压U_OC。

图2-93c为求入端电阻的等效电路。

R_O=（R₁∥R₃）+（R₂∥R₄）=[（2∥6）+（3∥3）]Ω=3Ω

最后化为AB端戴维南等效电路，如图2-93d所示。

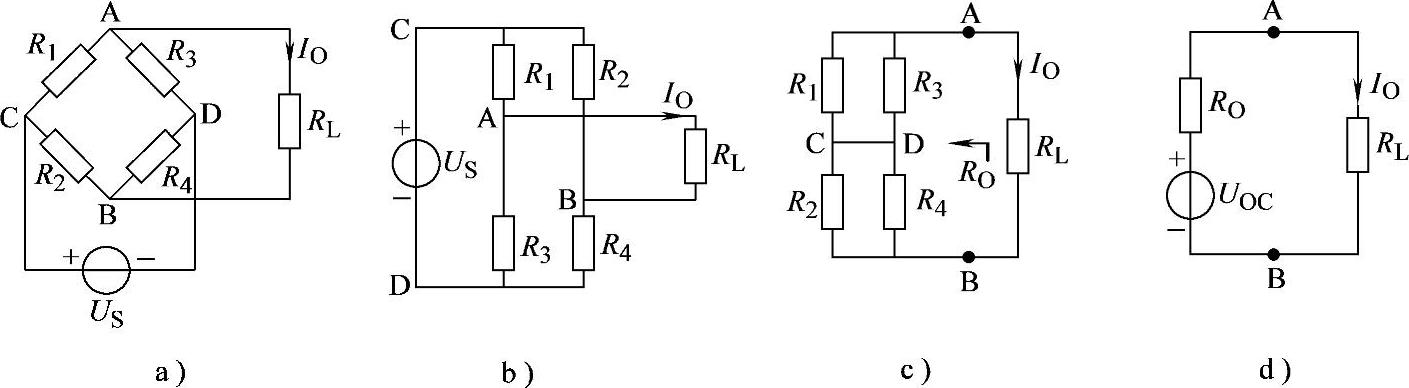
图2-93 习题2.65电路

2.66 已知电路如图2-94a所示，U_S1=20V，U_S2=10V，R₁=4Ω，R₂=6Ω，R₃=12.6Ω，R₄=10Ω，R₅=4Ω，R₆=6Ω，试用戴维南定理求解电阻R₃中电流I。

解：将R₁、R₂、U_S1、U_S2组成的部分电路等效为R₁₂、U_S组成的电路，将R₄、R₅、R₆组成的电阻网络等效为一个电阻R₄₅₆，因此图2-94a电路等效为图2-94b电路。

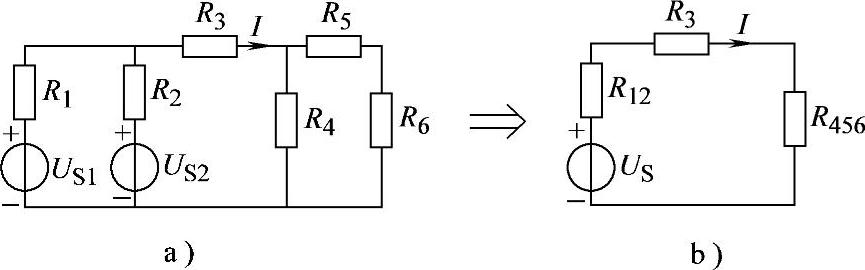
图2-94 习题2.66电路

R₁₂=R₁∥R₂=4∥6Ω=2.4Ω

R₄₅₆=R4∥（R₅+R₆）=[10∥（6+4）]Ω=5Ω

2.67 已知电路如图2-95a所示，试用戴维南定理求解I。

解：首先将电路改画成较容易看清连接关系的电路，如图2-95b所示，然后再求出其AB端等效电路，如图2-95c所示。

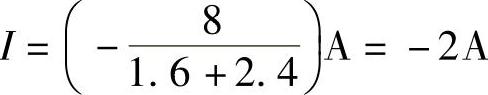
2.68 已知有源两端网络N的实验电路分别如图2-96a、b所示，试求该网络AB端戴维南等效电路。

解：图2-96a，开路电压U_OC=U_AB=100V

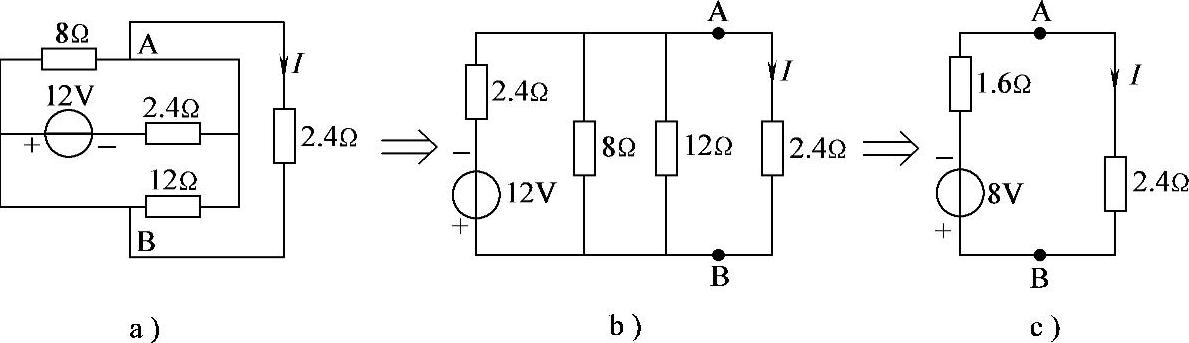
图2-95 习题2.67电路

图2-96b，，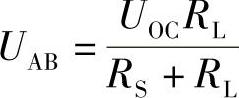

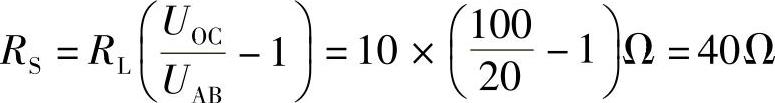
据此，画出该网络AB端戴维南等效电路如图2-96c所示。

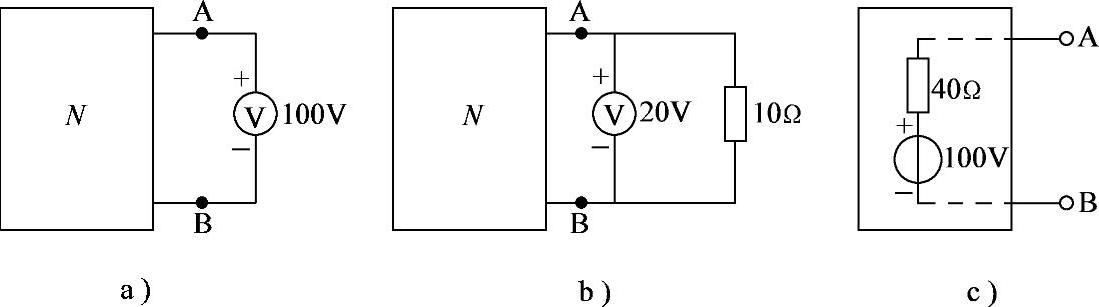
图2-96 习题2.68电路

2.69 测得一含源两端网络的开路电压为10V，短路电流为0.1A，试画出其戴维南等效电路。

解：开路电压即为该戴维南电路内电压源电压U_OC=10V。

戴维南电路内阻（或称入端电阻、输出电阻）：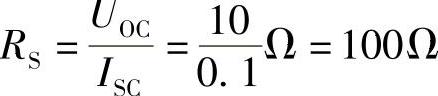

因此，画出戴维南等效电路如图2-97所示。

2.70 测得一含源二端网络的开路电压为50V，将R=20Ω的电阻接到该网络输出端，测得R两端电压为40V，试求该网络戴维南等效电路。

解：画出加负载20Ω的测试电路如图2-98a所示。

则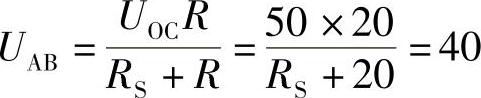：，解得 R_S=5Ω

据此，画出该网络戴维南等效电路如图2-98b所示。

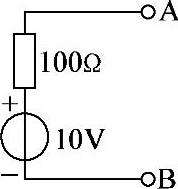
图2-97 习题2.69电路

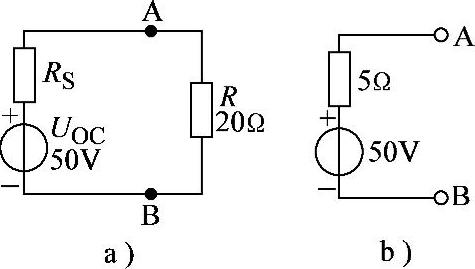
图2-98 习题2.70电路

2.71 已知某含源二端网络，测得其开路电压为100V，短路电流为10mA，试求：

（1）戴维南等效电路。

（2）外接负载R_L应为多大才能获得最大功率？最大功率是多少？

解：开路电压：U_OC=100V，即为其戴维南等效电路电压源电压。

内阻：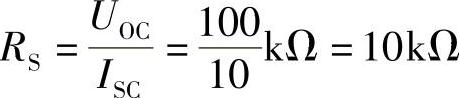

画出其戴维南等效电路如图2-99所示。

外接负载R_L=R_S=10kΩ时，能获得最大功率。

最大功率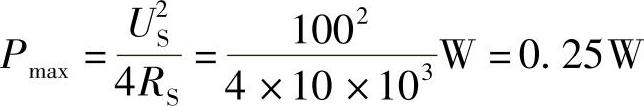

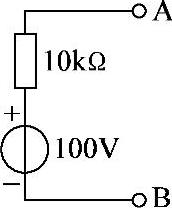
图2-99 习题2.71电路

2.72 已知电路如图2-100所示，R₁=6Ω，R₂=50Ω，R_L=5Ω，U_O=9.8V，试求U_I。

解：U_O=0.98IR_L，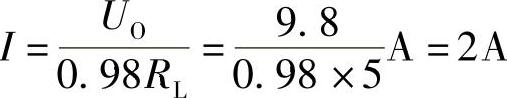

U_I=IR₁+（1-0.98）IR₂

=（2×6+0.02×2×50）V=14V

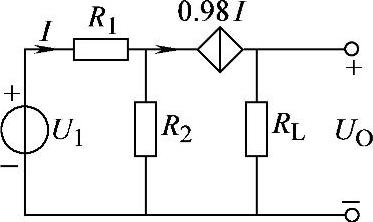
图2-100 习题2.72电路

2.73 已知电路如图2-101所示，R₁=6Ω，R₂=2Ω，I_S=4A，试求电流源I_S两端电压U_S。

解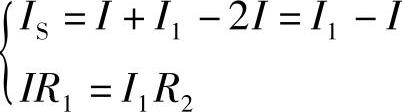：代入数据得：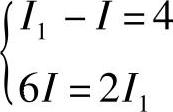

解得：I=2A

因此，U_S=IR₁=2×6V=12V

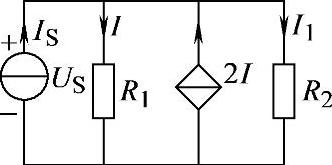
图2-101 习题2.73电路

2.74 已知电路如图2-102a所示，试求8Ω两端电压U。

图2-102 习题2.74电路

解：将图2-102a电路依次等效变换如下：

a）→b）：将受控电流源2I、2Ω等效为受控电压源；

b）→c）：2Ω与2Ω串联相加；

c）→d）：再将受控电压源4I，4Ω等效为受控电流源；

d）→e）：受控电流源I与独立电流源1A并联合并。

按分流公式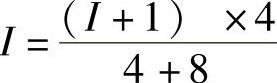：，解得：I=0.5A

U=8I=8×0.5V=4V

受控源电路在等效变换过程中，被控量可等效变换，但控制量不能等效变换，例如图2-102a中，8Ω中的电流I为控制量，而受控电流源2I则为被控量。

2.75 已知电路如图2-103a所示，R₁=R₂=R₃=10Ω，试求R₂两端电压U。

解：将图2-103a电路依次等效变换如下（控制量U支路不能改变）。

a）→b）：受控电流源0.5U、R₁等效为受控电压源；

b）→c）：10Ω与R₃串联相加；

c）→d）：再将受控电压源5U，20Ω等效为受控电流源；

d）→e）：受控电流源0.25U与独立电流源1.2A合并。

U=（1.2-0.25U）×（10∥20），解得U=3V

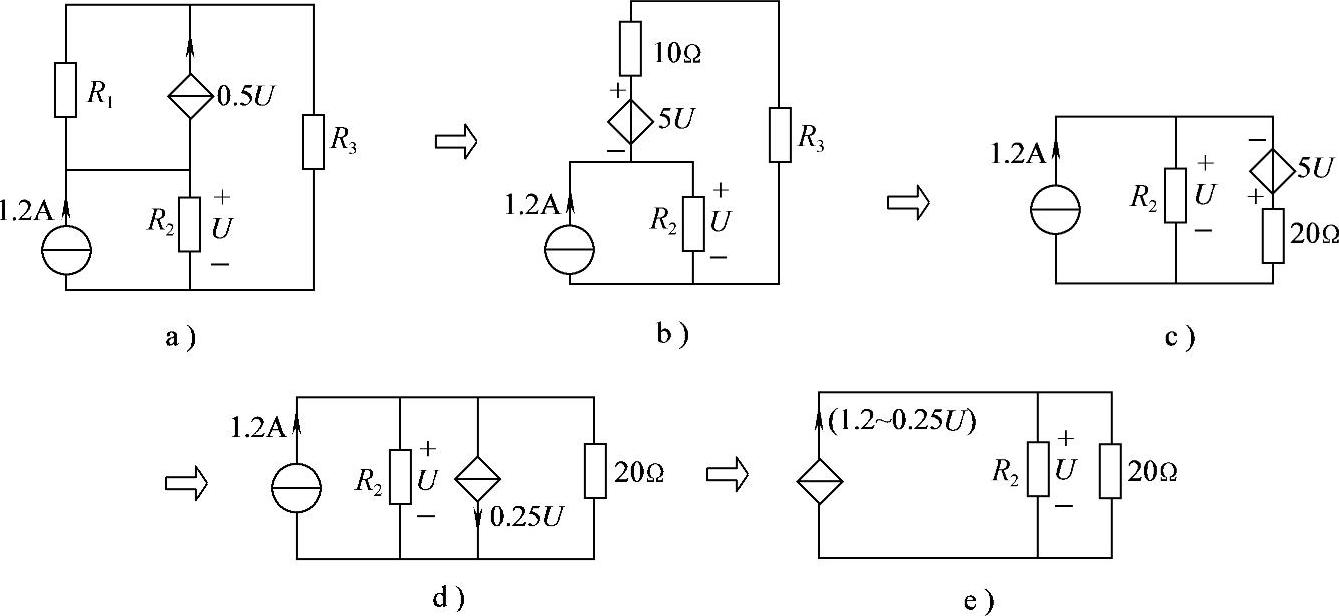
图2-103 习题2.75电路

2.76 已知电路如图2-104a所示，试求5Ω电阻两端电压U。

解：将图2-104a依次等效变换如下（控制量I₁支路不能改变）。

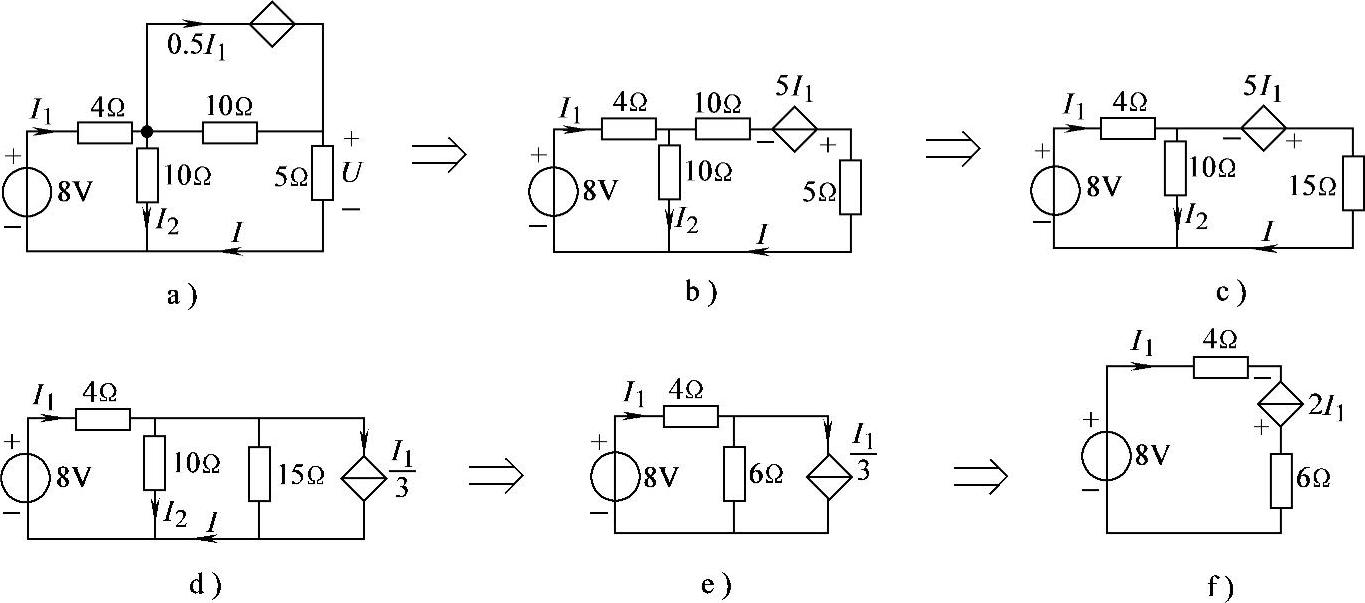
图2-104 习题2.76电路

a）→b）：受控电流源0.5I₁、10Ω等效为受控电压源；

b）→c）：10Ω与5Ω串联合并；

c）→d）：受控电压源5I₁，15Ω等效为受控电流源；

d）→e）：10Ω与15Ω并联合并；

e）→f）：受控电流源I₁/3、6Ω等效为受控电压源。

据此，列出KVL方程：（4+6）I₁=8+2I₁，解得：I₁=1A

从图2-104a可得：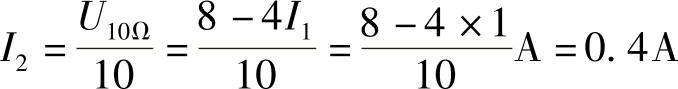

I=I₁-I₂=（1-0.4）A=0.6A

U=5I=5×0.6V=3V

2.77 已知电路如图2-105所示，R₁=R₂=10Ω，R₃=15Ω，U_S=37V，试求电流I。

解：参阅例2-9。

2.78 已知电路如图2-106所示，R₁=2Ω，R₂=3Ω，R₃=5Ω，试求ab端等效电路。

解：（1）先将图2-106a等效为图2-106b电路。

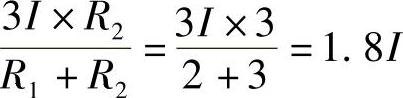
R₁∥R₂=2∥3Ω=1.2Ω

（2）列出图2-106bKVL方程：

U_ab=（1.2+R₃）I+1.8I=6.2I+1.8I=8I

上式表明，该电路为一个8Ω纯电阻，流过电流I时，两端电压为8I。据此画出等效电路如图2-106c所示。

2.79 已知电路如图2-107所示，U_S1=10V，R₁=2Ω，R₂=5Ω，R₃=3Ω，试求戴维南等效电路。

解：参阅例2-10。

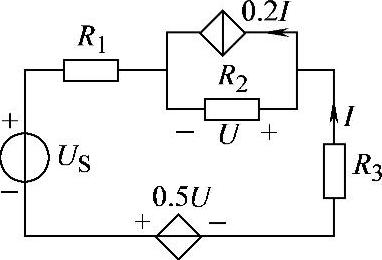
图2-105 习题2.77电路

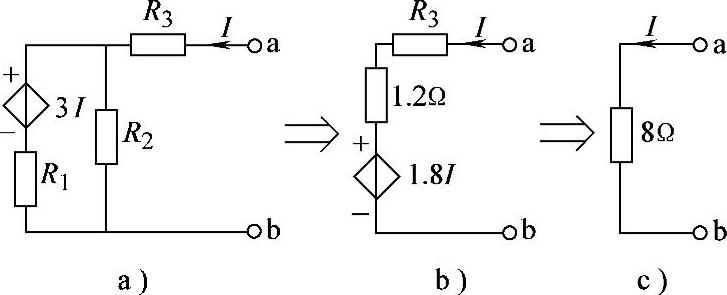
图2-106 习题2.78电路

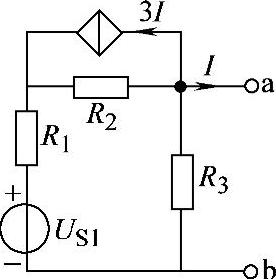
图2-107 习题2.79电路

2.80 已知电路如图2-108a所示，I_S1=2.5A，I_S2=5A，R₁=5Ω，R₂=4Ω，R₃=2Ω，试求解U₁、I₃。

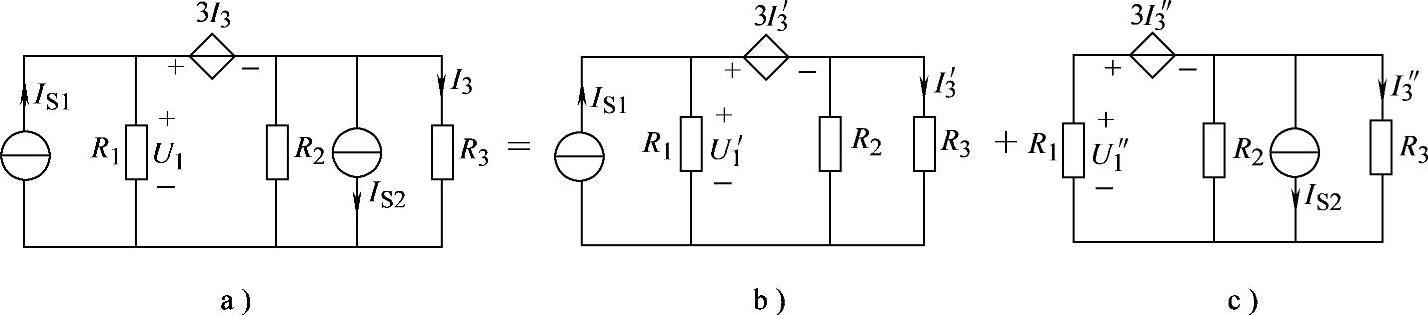
图2-108 习题2.80电路

解：根据KCL，有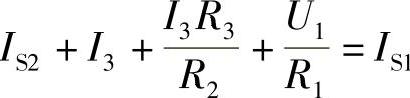：，即：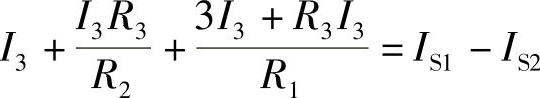

代入数据得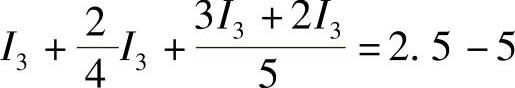：，解得：I₃=-1A

U₁=3I₃+I₃R₃=3I₃+2I₃=5I₃=5×（-1）V=-5V

2.81 已知电路与参数同上题，试用叠加定理求U₁、I₃。

解：画出叠加定理求解电路如图2-108b、c所示。

（1）图2-108b中：U′₁=3I′₃+I′₃R₃=3I′₃+2I′₃=5I′3

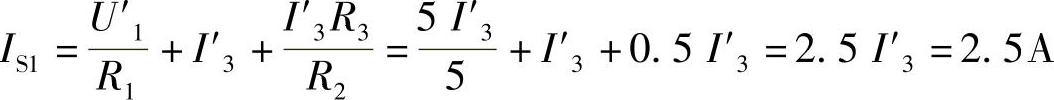
I′₃=1A，U′₁=5I′₃=5×1V=5V

（2）图2-108c中：根据弥尔曼定理，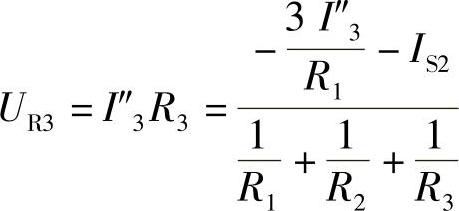

代入数据得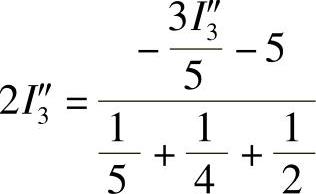：，解得I₃″=-2A

U″₁=3I″₃+R₃I″₃=5I″₃=5×（-2）V=-10V

U₁=U₁′+U″₁=（5-10）V=-5V

I₃=I₃′+I₃″=（1-2）A=-1A

2.82 已知电路如图2-109a所示，U_S1=-4V，I_S2=2A，R₁=R₂=2Ω，R₃=3Ω，试用叠加定理求I。

解：画出叠加定理求解电路如图2-109b、c所示。

（1）图2-109b中：U_S1=I′R₃+5U₁-U₁=I′R₃+4U₁=I′R₃+4（-I′R₁）=I′（R₃-4R₁）

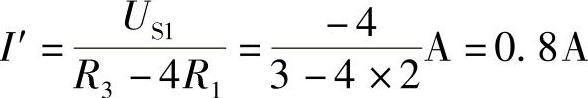
（2）图2-109c中：U₁=I″R₃+5U₁，即：I″R₃+4U₁=0，I″R₃+4（I_S2-I″）R₁=0

解得：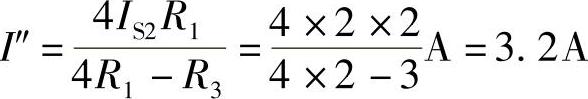

I=I′+I″=0.8+3.2=4A

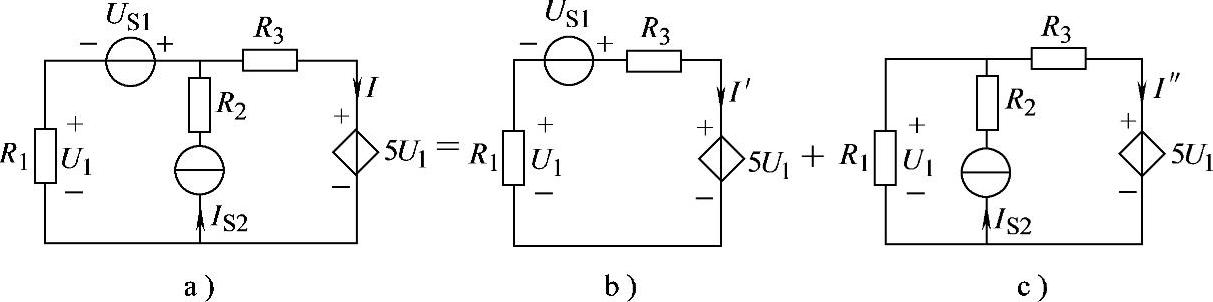
图2-109 习题2.82电路