典型例题解析：电路串、并联及叠加定理应用

【例2-1】已知电阻混联电路如图2-15a所示，R₁=R₅=R₆=R₇=6Ω，R₂=R₃=R₄=9Ω，试求电路等效电阻R。

图2-15 例2-1电路

解：初看图2-15a电路，一下很难看清电路电阻串、并联的结构，一般可按下列步骤操作：

（1）标节点。如图2-15b所示，将所有连接点用字母标明。

（2）编序号。编序号的原因是有的题目没给出电阻序号，仅给出电阻阻值，而部分电阻的阻值是相同的，在下一步骤改画电路时无法区分。且即使电阻阻值不同，改画电路时也难免遗漏。图2-15a电路的电阻已编序号。

（3）改画电路。改画电路的方法是按已标明的电路连接点依次画出电路。

①如图2-15b中，从节点A到节点B，第一条支路R₁，画出R₁；第二条支路是ACB，两者关系是并联。

②从节点A到节点C，有两条支路R₂和R₃，如图2-15c所示，终节点为C，始节点为A，因此，R₂与R₃的连接关系为并联，画出R₂和R₃。

③从节点C到节点B，有两条支路，其中一条是通过R₄直接到B，另一条是CDB，两者关系是并联，画出R₄。

④从节点C到节点D，有两条支路R₅和R₆，始节点为C，终节点为D，因此R₅与R₆的连接关系为并联，画出R₅和R₆。

⑤从节点D到B，有一条支路R₇。

至此电路改画完毕，如图2-15c所示。在改画电路过程中，若一次看不清电路连接关系，可多次改画，直到按习惯画法能看清电路串并联结构。

（4）计算等效电路：

R=R₁∥{（R₃∥R₂）+R₄∥[（R₅∥R₆）+R₇]}

=6∥{（9∥9）+9∥[（6∥6）+6]}Ω=3.6Ω

【例2-2】已知电路如图2-16所示，R₁=R₂=R₃=9Ω，R₄=R₅=R₆=3Ω，试求OA端和AB端等效电阻。

解：初看电路，连接关系似乎较为复杂，为便于观察分析，改画电路：OA端电路如图2-16b所示，AB端电路如图2-16d所示。

（1）OA端电路利用Y-△变换求解可有多种方法，其中R₁、R₂、R₃组成的△形联结电路属于对称△形联结，转换计算较为方便。转换为R₇、R₈、R₉组成的对称Y形联结电路，如图2-16c所示。

R₇=R₈=R₉=R₁/3=3Ω

R_OA=R₄∥{[（R₅+R₇）∥（R₆+R₈）]+R₉}=3∥{[（3+3）∥（3+3）]+3}Ω=2Ω

（2）AB端电路利用Y-△变换求解方法也有多种，其中R₄、R₅、R₆组成的Y形联结电路为对称Y形电路，转换为R₁₀、R₁₁、R₁₂组成的对称△形电路，如图2-16e所示。

R₁₀=R₁₁=R₁₂=3R₄=9Ω

R_AB=R₁∥R₁₀∥[（R₃∥R₁₁）+（R₂∥R₁₂）]=9∥9∥[（9∥9）+（9∥9）]Ω=3Ω

从上例中我们可以得出两个结论：

①同一电阻网络，从不同端点看进去的等效电阻有可能是不同的。

②利用Y-△变换求解等效电阻的方法可能有多种，但选择对称Y形或对称△形可简化求解过程。

本例OA端等效电阻还有一种解法。图2-16b中，由于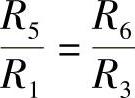，因此，U_B=U_C，即B点与C点是等电位点。等电位点之间可以按需作开路处理（因B点与C点之间无电流，相当于开路），如图2-16f所示；也可按需作短路处理（因B点与C点电位相等，相当于短路），如图2-16g所示。

BC作短路处理时，R_OA=R₄∥（R₅+R₁）∥（R₆+R₃）=[3∥（9+3）∥（9+3）]Ω=2Ω

BC作开路处理时，R_OA=R₄∥[（R₅∥R₆）+（R₁∥R₃）]=3∥[（9∥9）+（3∥3）]Ω=2Ω

图2-16 例2-2电路

【例2-3】已知电路如图2-17a所示，试将其等效为一个电压源电路。

解：先将两个电压源等效为两个电流源，如图2-17b所示；再将两个并联的电流源合并为一个电流源，如图2-17c所示，最后将其转换为一个电压源，如图2-17d所示。

图2-17 例2-3电路

从上例中我们可悟出：电压源与其他元件（理想电流源、电阻或实际电压源）并联时，可将电压源等效转换为电流源，然后分别利用理想电流源并联、电阻并联的方法等效转换为一个理想电流源与一个电阻并联的电路。

【例2-4】已知电路如图2-18a所示，试将其等效为一个电流源电路。

解：先将两个电流源等效为两个电压源，如图2-18b所示；再将两个串联的电压源合并为一个电压源，如图2-18c所示；最后将其转换为一个电流源，如图2-18d所示。

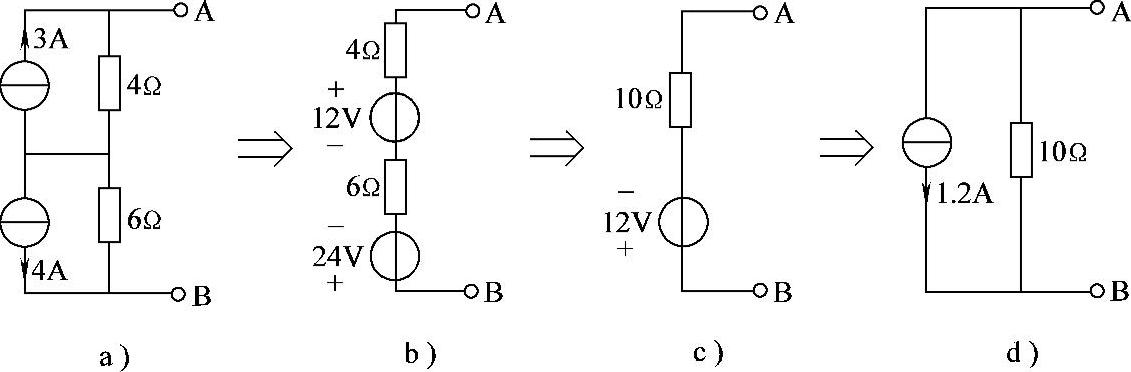
图2-18 例2-4电路

从上例中我们可悟出：电流源与其他元件（理想电压源、电阻或实际电流源）串联时，可将电流源等效转换为电压源，然后分别利用理想电压源串联、电阻串联的方法等效转换为一个理想电压源与一个电阻串联的电路。

【例2-5】已知电路如图2-19所示，试以O为参考节点，列出A、B节点电压方程。

解：列出节点电压方程如下，其中R₅与电流源I_S5串联，对外电路不起作用，因此不需列入节点电压方程。

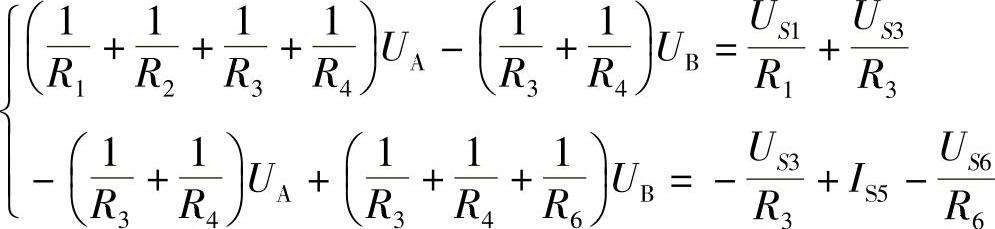(www.xing528.com)

【例2-6】已知电路如图2-20所示，R₁=10Ω、R₂=50Ω、R₃=40Ω、U_S1=28V、U_S2=5V，试分别用支路电流法、网孔电流法和弥尔曼定理求解支路电流I₁、I₂和I₃。

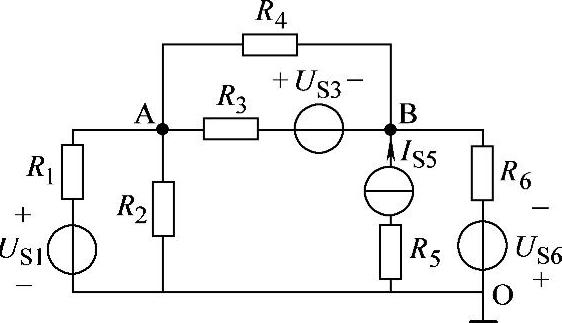
图2-19 例2-5电路

图2-20 例2-6电路

解：（1）支路电流法。

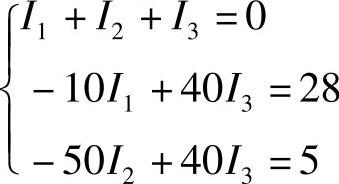代入数据得联立求解得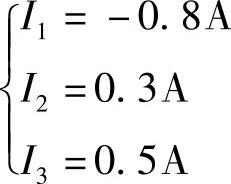

（2）网孔电流法。

画出网孔电流I_a、I_b及其绕行方向。

代入数据得联立求解得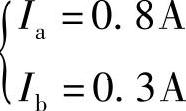

因此：I₁=-I_a=-0.8A，I₂=I_b=0.3A，I₃=I_a-I_b=0.8-0.3=0.5A

（3）弥尔曼定理。

标出节点A、B，则有

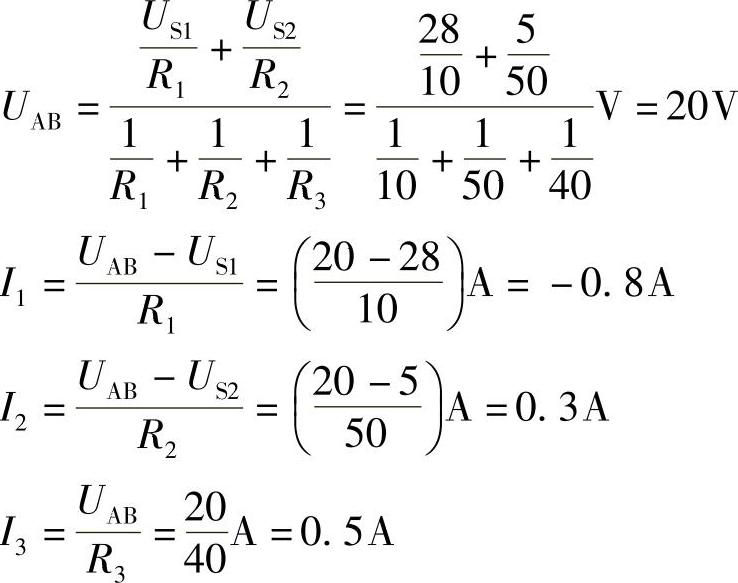
比较上述三种解题方法，可得出：求解两个节点的电路，一般用弥尔曼定理最方便。

【例2-7】已知电路如图2-21a所示，U_S=10V，I_S=2A，R₁=5Ω，R₂=R₃=3Ω，R₄=2Ω，试用叠加定理求解I₁，I₂。

图2-21 例2-7电路

解：画出叠加定理求解电路如图2-21b、c、d所示，其中图d是图c的另一种画法，更便于看清电路连接关系。

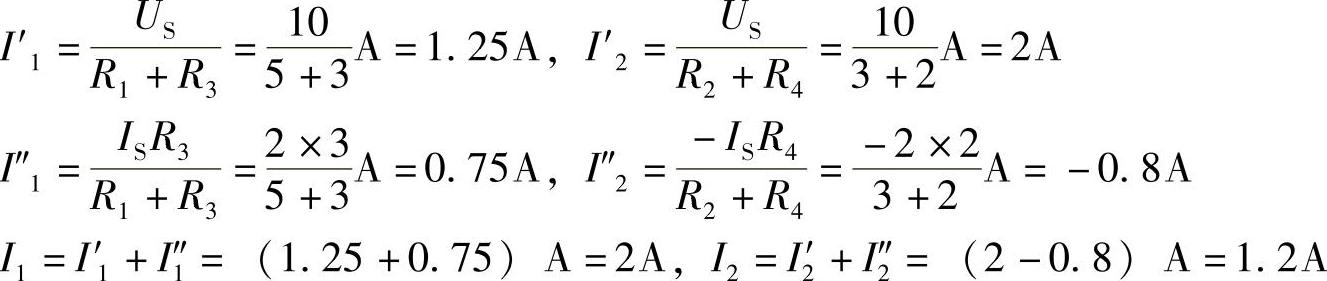
【例2-8】已知电路如图2-22a所示，R₁=1Ω，R₂=2Ω，R₃=3Ω，R₄=4Ω，R_L=5Ω，U_S=6V，试用戴维南定理求电阻R中的电流I。

解：若先求出图2-22a电路AB端的戴维南等效电路，如图2-22b所示，则I不难求出。

求U_OC时，按戴维南定理，将AB端外电路开路，并改画电路如图2-22c所示。

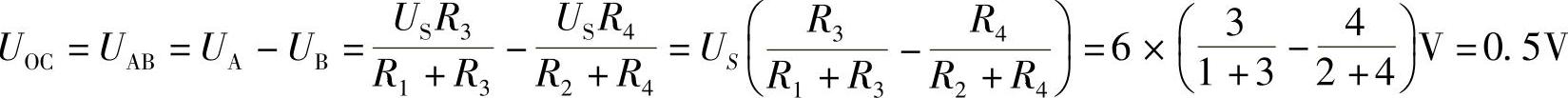
求R_O时，按戴维南定理，将U_S短路，并改画电路如图2-22d所示。

R_O=（R₁∥R₃）+（R₂∥R₄）=[（1∥3）+（2∥4）]Ω=2.08Ω

因此，

图2-22 例2-8电路

【例2-9】已知电路如图2-23所示，R₁=R₂=10Ω，R₃=15Ω，U_S=37V，试求电流I。

解：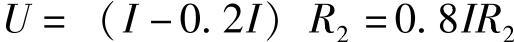

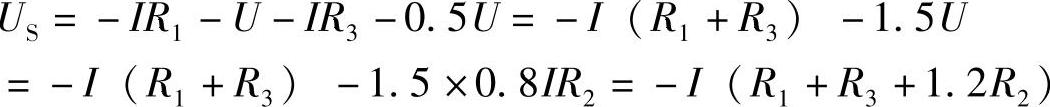
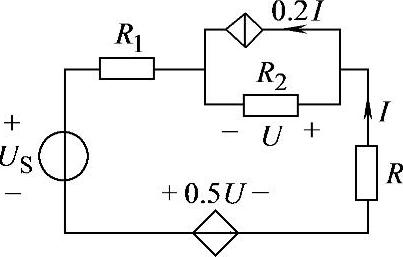
图2-23 例2-9电路

【例2-10】已知电路如图2-24a所示，U_S1=10V，R₁=2Ω，R₂=5Ω，R₃=3Ω，试求戴维南等效电路。

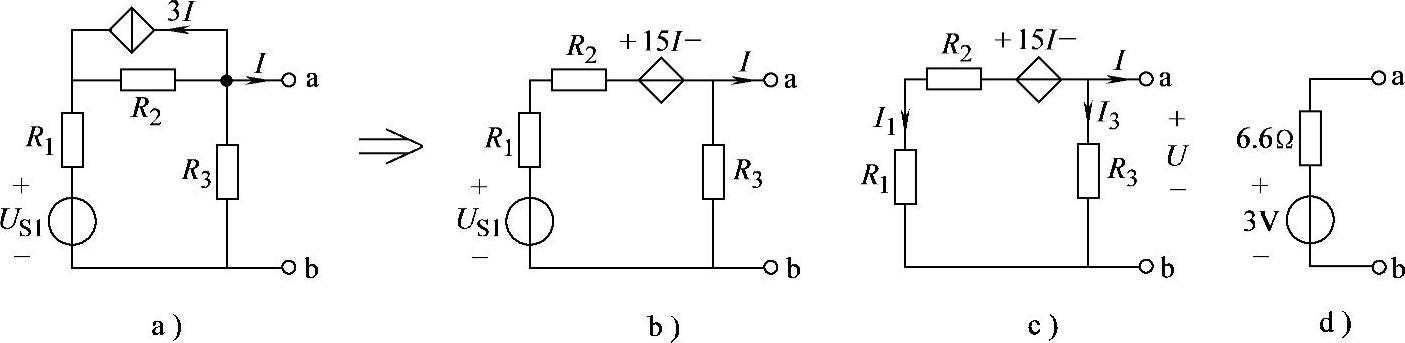
图2-24 例2-10电路

解：将图2-24a电路中的受控电流源转换为受控电压源，如图2-24b所示。

（1）求戴维南等效电路开路电压时，I=0，则受控电压源15I=0，开路电压即为R₃上分得的电压。

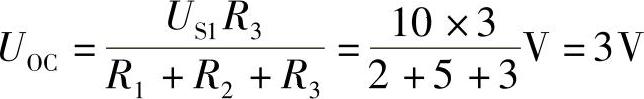
（2）求戴维南等效电路入端电阻时，网络内电压源U_S1应短路，并设在ab端外加电压U，端口电流为I，如图2-24c所示。则有：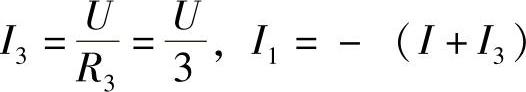

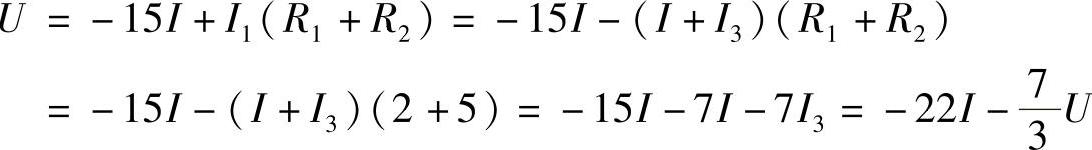
解得：，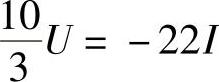

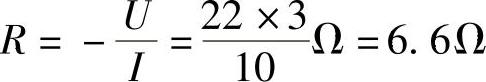
据此，画出戴维南等效电路如图2-24d所示。