1.网孔电流法
一般形式(双网孔):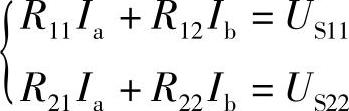
(1)自阻R11、R22:网孔中所有电阻之和,自阻总是正的。
(2)互阻R12、R21:相邻网孔的公共电阻,若网孔电流均取顺时针方向,则互阻为负。
(3)US11、US22:网孔中电压源电压的代数和,电压源的电压参考方向与网孔电流一致时取“-”号,相反时取“+”号。
例如,对图2-9电路的网孔电流方程可写为:
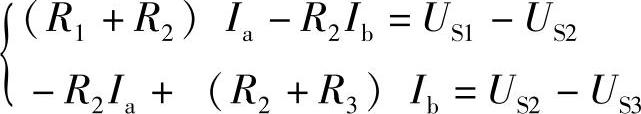
2.节点电压法
一般形式(3节点):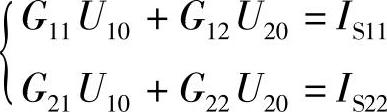
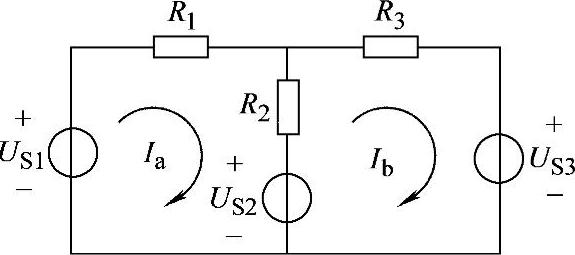
图2-9 网孔电流法示意图
(1)自导G11、G22:与变量节点相联所有支路电导之和,自导总是正的。
(2)互导G12、G21:相邻变量节点之间支路电导之和,互导总是负的。
(3)IS11、IS22:流经变量节点的电流之和,流进节点取“+”号,流出节点取“-”号。
例如,对图2-10电路节点电压方程可写为:
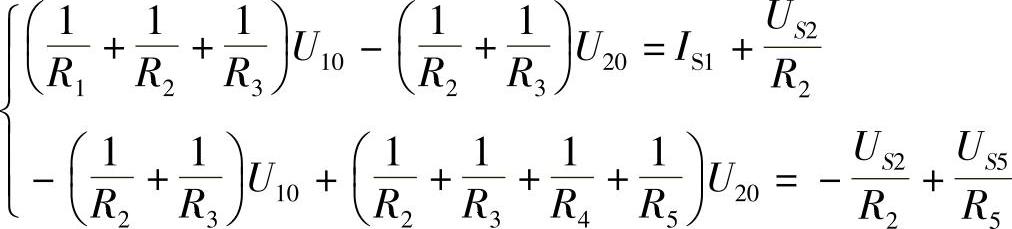
3.弥尔曼定理
弥尔曼定理是求解两个节点电路的节点电压法。
一般形式: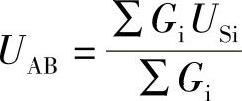
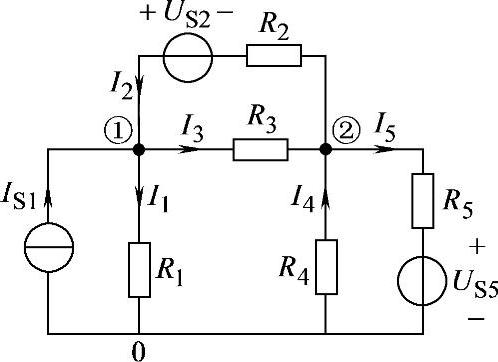
图2-10 节点电压法示意电路
(1)∑GiUSi:指向节点A的总电流,流进节点A取“+”号,流出节点A取“-”号。
(2)∑Gi:节点总电导,等于各支路电阻倒数之和。
例如,对图2-11电路节点电压方程可写为:(https://www.xing528.com)
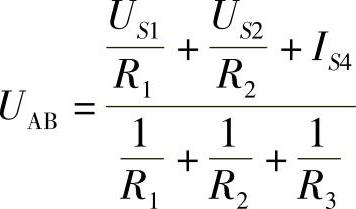
4.叠加定理
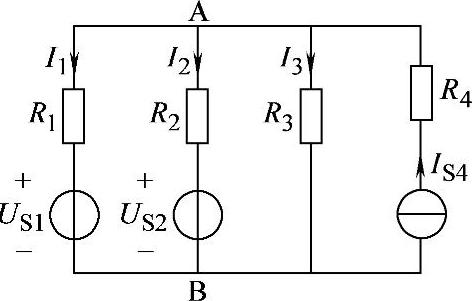
图2-11 节点电压法电路
有多个独立电源共同作用的线性电路,任一支路电流(或电压)等于每个电源单独作用时在该支路产生的电流(或电压)的代数和(叠加)。
例如,对图2-12电路,有两个电源US和IS共同作用,支路电流I1和I2可分别由电压源US单独作用时产生的I1′、I2′(如图2-12b所示)和由电流源IS单独作用时产生的I″1、I″2(如图2-12c所示)叠加而成,即I1=I1′+I″1,I2=I2′+I″2。
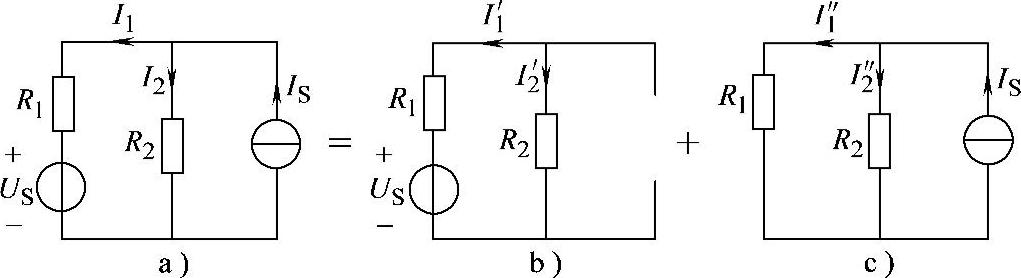
图2-12 叠加定理示意图
注意
(1)叠加定理只能用来计算线性电路的电流和电压,不适用计算电路功率或非线性电路。
(2)不作用电源处理:电压源短路,电流源开路。
(3)为便于求解,宜画出叠加定理求解电路,且电路格式、元件位置和电流(或电压)参考方向以不变为宜,此时求代数和(叠加)时,均取“+”号,不易出错。
5.齐性定理
在线性电路中,若激励(指独立电压源和独立电流源)同时增大或同时缩小K倍(K为实常数),则电路响应(指各支路电流或电压)也将同样增大或缩小K倍。
齐性定理描述了线性电路的比例特性,特别适用于分析梯形电路。
6.戴维南定理
任何一个线性含源二端电阻网络NS(如图2-13a所示),对外电路来讲,都可以用一个电压源和一个电阻相串联的模型(如图2-13b所示)等效替代。电压源的电压等于该网络NS的开路电压uOC(如图2-13c所示);串联电阻等于该网络内所有独立源置零(独立电压源短路,独立电流源开路)后所得无源二端网络的等效电阻(或称为入端电阻、输出电阻)RO(如图2-13d所示)。
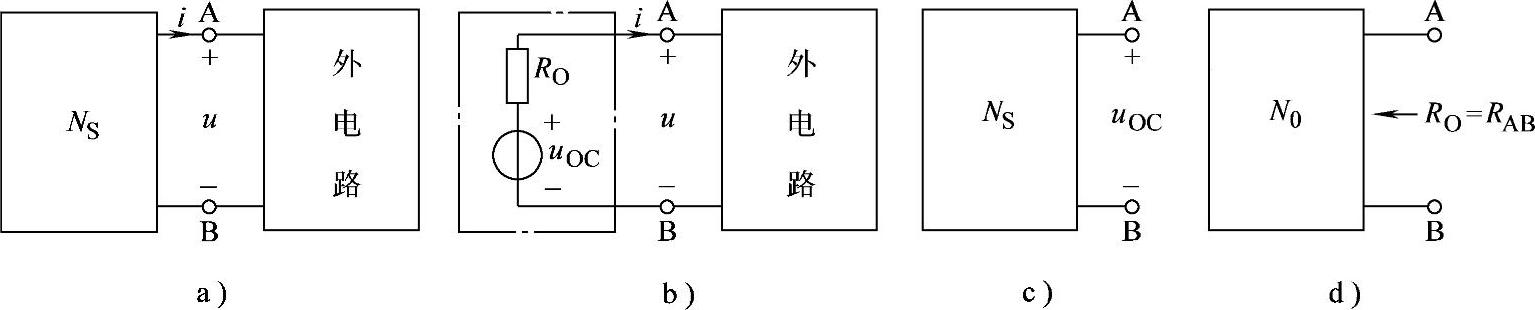
图2-13 戴维南定理示意图
7.最大功率传输(见图2-14)
条件:RL=RO(称为负载与信号源阻抗匹配)
负载最大功率: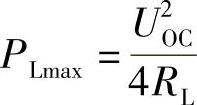
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




