典型例题解析：电路KCL、功率计算与基础概念

【例1-1】已知电路如图1-4所示，R₁=2Ω，R₂=6Ω，R₃=4Ω，U_S1=20V，U_S3=26V，试求支路电流I₁、I₂、I₃。

解：（1）设定回路Ⅰ和回路Ⅱ的绕行方向，如图1-4所示。

（2）列出回路KVL方程：

回路Ⅰ：I₁R₁-I₂R₂-U_S1=0

回路Ⅱ：I₂R₂-I₃R₃+U_S3=0

（3）列出节点A的KCL方程：I₁+I₂+I₃=0

（4）代入数据，联立求解方程组得：I₁=1A，I₂=-3A，I₃=2A

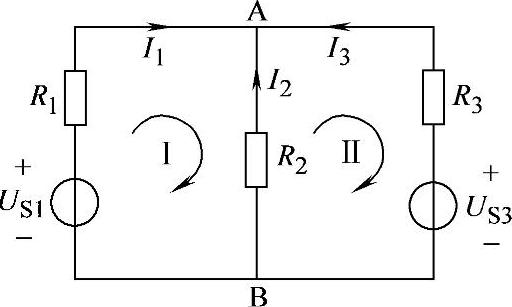
图1-4 例1-1电路

说明：1）回路绕行方向即为电压电流关联参考方向，列回路KVL方程时正负号取法均按此关联参考方向处理。

2）根据KCL，还可列出节点B的KCL方程：-I₁-I₂-I₃=0，但该方程可由节点A的KCL方程移项而得，不是独立方程。对于具有n个节点的电路，只能列出（n-1）个独立的节点电流方程。

3）根据KVL，还可列出由元件U_S1、R₁、R₃、U_S3组成的回路（即由回路Ⅰ、Ⅱ组成的大回路）的KVL方程：I₁R₁-I₃R₃+U_S3-U_S1=0，但该方程可由回路Ⅰ、回路Ⅱ的KVL方程相加而得，不是独立方程。对于具有m条支路、n个节点的电路，只能列出[m-（n-1）]个独立KVL方程。

4）支路电流法可推广应用于更多节点、更多回路的电路求解各支路电流。支路电流法是最基本的电路分析方法。

【例1-2】已知电路如图1-5所示，R₁=R₂=R₃=R₄=R₅=R₆=2Ω，I_S1=1A，U_S2=2V，U_S3=4V，U_S4=6V，U_S5=8V，U_S6=10V，试以o点为参考点，求φ_a、φ_b、U_ab。

解：（1）选定回路电流I参考方向，如图1-5所示。

（2）列出回路KVL方程，并求解回路电流I：

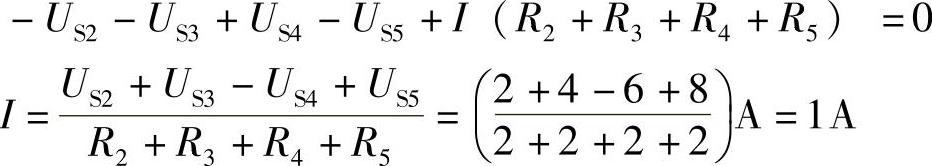
（3）求φ_a、φ_b、U_ab：

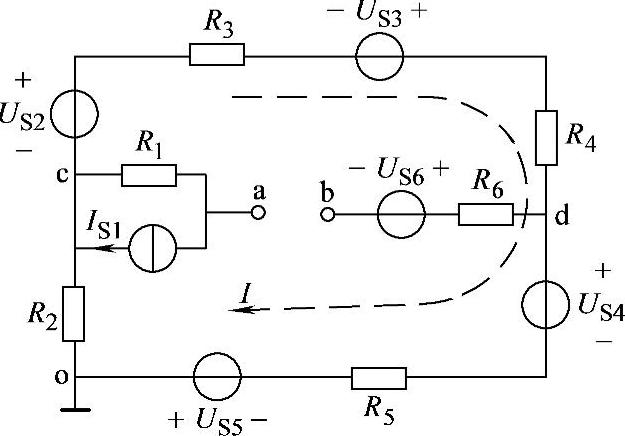
图1-5 例1-2电路

φ_a=U_ac+U_co=-I_S1R₁-IR₂=（-1×2-1×2）V=-4V

φ_b=U_bd+U_do=-U_S6+U_S4+IR₅-U_S5=（-10+6+1×2-8）V=-10V（注：bd支路中无电流，R₆压降为0）

φ_b也可另解：φ_b=U_bd+U_dc+U_co=-U_S6-IR₄+U_S3-IR₃+U_S2-IR₂

=[-10-1×（2+2+2）+4+2]V=-10V

U_ab=φ_a-φ_b=[-4-（-10）]V=6V(www.xing528.com)

说明：从求解φ_b的两种方法中可得出：两点间电压是定值，与计算时所沿路径无关。

【例1-3】已知电路如图1-6所示，U_S=10V，I_S=1A，R=5Ω，试求各元件功率，并指出其发出或吸收功率。

解：（1）图1-6a电路。

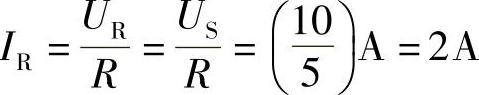
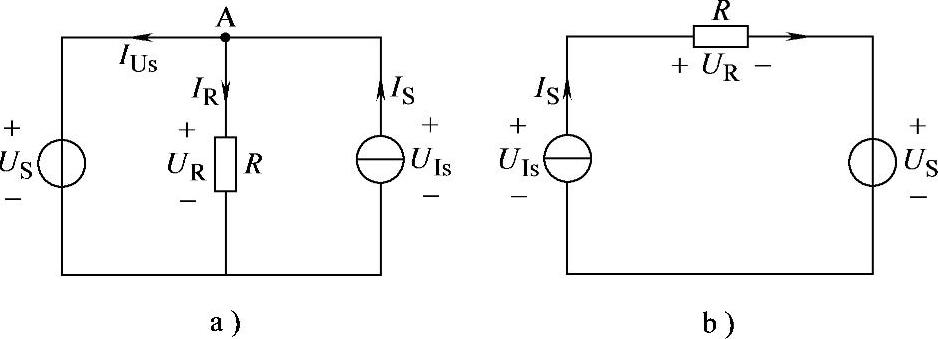
图1-6 例1-3电路

根据KCL，对于节点A：I_S=I_R+I_Us

解得：I_Us=I_S-I_R=（1-2）A=-1A

电阻功率：P_R=U_RI_R=U_SI_R=（10×2）W=20W，P_R为正值，吸收功率。

电压源功率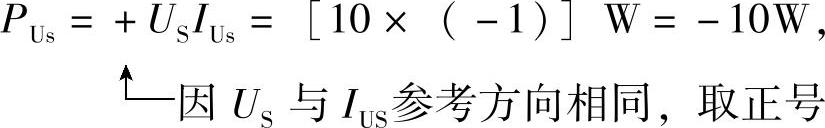：P_Us为负值，发出功率。

电流源功率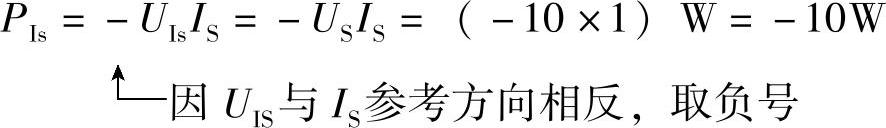：，P_Is为负值，发出功率。

P_R=P_Is+P_Us，吸收功率=发出功率，功率平衡。

（2）图1-6b电路。

U_R=I_SR=（1×5）V=5V

根据KVL，U_Is=U_R+U_S=（10+5）V=15V

电阻功率：P_R=U_RI_R=U_RI_S=（5×1）W=5W，P_R为正值，吸收功率。

电压源功率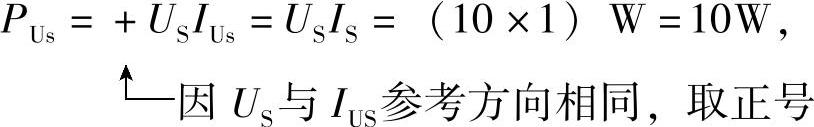：P_Us为正值，吸收功率。

电流源功率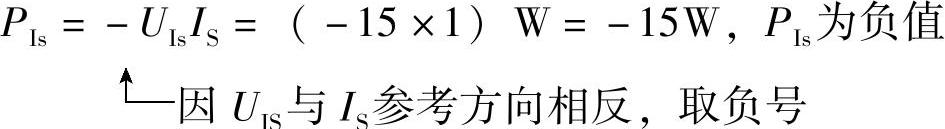：，发出功率。

P_R+P_Us=P_Is，吸收功率=发出功率，功率平衡。

说明：1）电阻为耗能元件，其功率恒为正值。若计算出来的电阻功率为负值，则肯定出错。

2）电压源和电流源虽是电源，但在电路中不一定是发出功率，有时也会吸收功率，如图1-6b电路中的电压源。

3）在一个完整的电路中，各元件的吸收功率之和必然等于各元件的发出功率之和，整个电路的吸收功率等于发出功率，称为功率平衡。这一条也可作为检验计算功率是否有误的标准之一。

4）例1-3是一道很典型的题目，涉及内容包括欧姆定律、KVL、KCL、电流电压参考方向和吸收功率、发出功率等基本概念，很有必要彻底搞清。求解此类题目时，对于图1-6a电路，属3个元件并联电路。并联电路的特点是元件两端电压相等，等于电压源已知电压值，可利用欧姆定律和KCL求出各支路电流，然后求解各元件功率。对于图1-6b电路，属3个元件串联电路。串联电路的特点是流过元件的电流相等，等于电流源已知电流值，可利用欧姆定律和KVL求出电阻R和电流源两端电压，然后求解各元件功率。