数据查表方法的基本理论及方法详解

通过前述吸收定律和探测器设计原理分析，传感器的两个通道的输出信号U_Ref和U_Act分别与等效原理的入射光强和被吸收后的光强成正比，即

式中 I——被测气体存在的情况下，被气体吸收后的发光强度；

I_o——目标气体不存在的情况下，一般在氮气条件下测得的，相当于光源的光强。

从第2章的红外辐射的吸收定律——朗伯-比尔定律，为了适应本章的模型，将其参数和形式变形后如下：

I=I_oexp（-KCⁿL） （6-2）

式中 K——比例因子，取决于气体浓度在吸收光谱区域内的吸收线选取以及滤光片的带宽关系；

L——气体入射光程；

n——修正常数，依赖于光程与被测气体的成分；

I——透射光强，即由目标气体吸收后的光强；

I_o——入射光强；(https://www.xing528.com)

C——被测气体的物质浓度。

由以上两式分析，可以建立一个重要的数学式来分析气体的浓度，首先从建立下面的等式阐述入手，这是一个重要关系式，根据第2章阐述的气体浓度透射率关系，下面这个关系式可定义为相对吸收率（Fractional absorbance，Fa）。

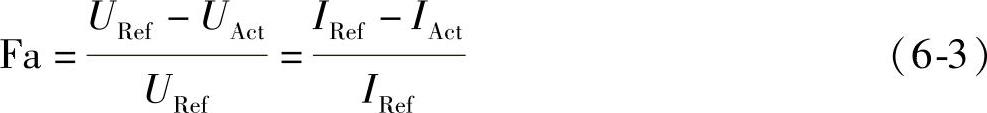
因此得出一个计算气体浓度的重要公式：

从这个关系式中分析，只要确定K、L、Fa三个参数，气体浓度C便可以求得，然而在实际的测试过程中，Fa是可以通过式（6-3）中两个探测器的输出信号来求得的，而K、L两个参数难以直接测量，但对于一个设计好的测量系统，KL的乘积是个常量，这在前述理论部分已阐述。从数学角度来分析式（6-4），如果能得到一组关于相对吸收率Fa与气体浓度C之间关系数据，那么显然式（6-4）是可以用描点法来确定它的大致关系，至于它的逼真程度，取决于点选取的多小，从这一思想出发，即可设计数据查表的方法来计算气体的浓度，下面将详细探讨查表方法的具体计算过程。

对于式（6-4），首先可以通过试验方法来估算确定K、L、n三个参数的值，来仿真Fa与C之间的大致关系，比如实验过程中，以甲烷为测试对象，获得了图6-4所示的曲线关系。从图中可以直观地看出，气体浓度处在低浓度时，相对吸收率Fa上升比较陡峭，随着浓度增大，相对吸收率Fa趋向于平坦化而达到饱和状态。因此，可以推断出：在低浓度情况下，测试的准确度要高，测试结果会更接近于真实值，而高浓度则反之。

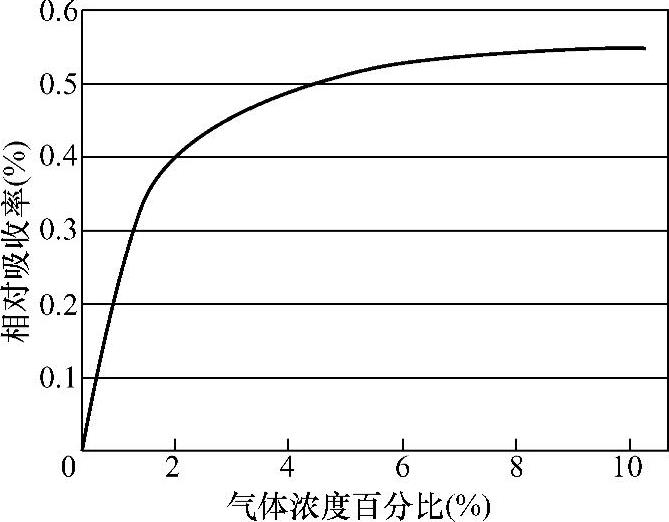
图6-4 相对吸收率Fa与气体浓度C之间的关系（甲烷）