电气传动的能量指标解析

电气传动的用电量接近全部发电量的2/3，如何有效地利用这些能量具有巨大的经济意义。电气传动的电源主要是来自50Hz的交流电网，电网向传动装置提供有功功率，用于驱动工作机械和支付机电的损失。有些传动装置可以把制动的能量回馈到电网。

需要提出能量的效率这一概念来分析电气传动装置的能量利用的状况。能量效率代表输出的有用能量P_out与输入能量P_in之比，或者有效能量P_eff与全部消耗能量P_exp之比：

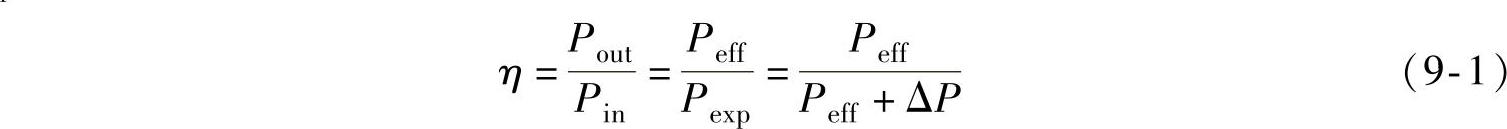
式中 ΔP——传动设备的能量损失，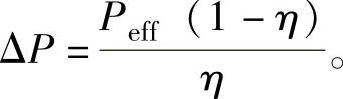

电气传动设备的功率部分由供电设备、变流器、电动机构成，因此，电气传动设备的总效率也和这些构成要素的效率有关，总效率等于各个组成部分的效率的乘积，即

η=η_ps·η_con·η_mot

式中的下标分别代表电源、变流器和电动机。

电动机的效率是轴上输出功率与电动机输入功率之比，即

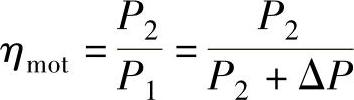
0.1～15kW的异步电动机的额定效率为0.85～0.9。随着电动机的功率增加，效率也逐渐提高，1000kW以上的异步电动机效率可达到0.97左右。

电动机的效率和轴上的负载大小有关，为了分析这种关联程度，把损失ΔP分为可变损失V和不变损失K

ΔP=K+V （9-2）

不变损失是在恒定转速时的损失，其中包括铁损、电动机自带冷却风机的损失以及附加损失（固定的摩擦损失、直流电动机的励磁绕组损失等）。可变损失是指跟负载大小有关的损失，这种损失和绕组电流的平方成正比，对于直流电动机，可变损失为V=I²_aR_a。对于交流异步电动机，定子绕组和转子绕组的损失共同构成可变损失，即V=3I²₁r₁+3I²₂r₂。

根据式（6-8），异步电动机转子绕组侧的损失为

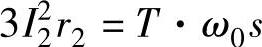
可以认为定子绕组的损失与转子绕组的损失之比值为r₁/r′₂，于是异步电动机的可变损失为

例题9.1 Y180-4异步电动机的数据为：P_N=22kW，n_N=1461r/min（即ω=153rad/s），η_N=0.89，r₁/r′₂=0.6。求在50%负载情况下电动机的效率。

解：1.电动机在额定状态下的损失为

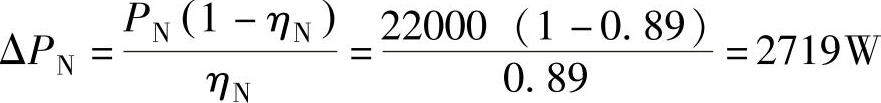
2.额定状态下的可变损失为

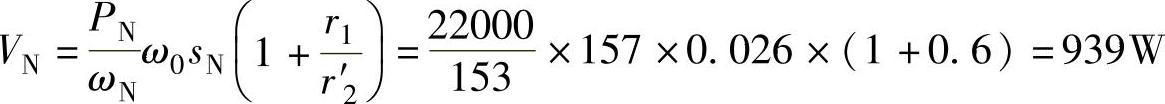
3.不变损失为

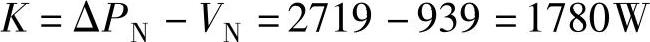
4.当负载情况为T_L=0.5T_N时，s=0.5s_N，这时的可变损失为

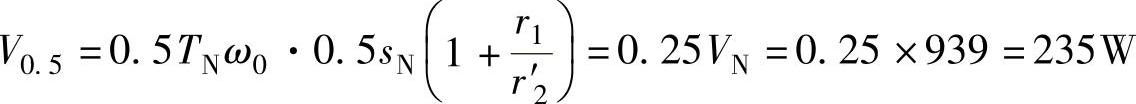
5.这时电动机的损失为(www.xing528.com)

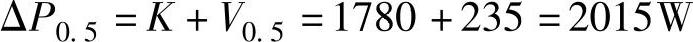
6.这时电动机的效率为

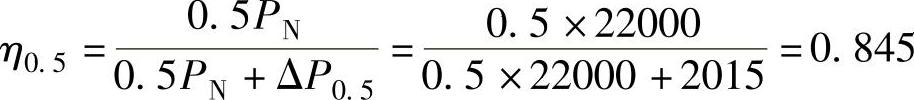
从这道例题可以看出，电动机的负载不饱满时，效率略有下降。典型的效率与负载的关系曲线如图9-1所示。

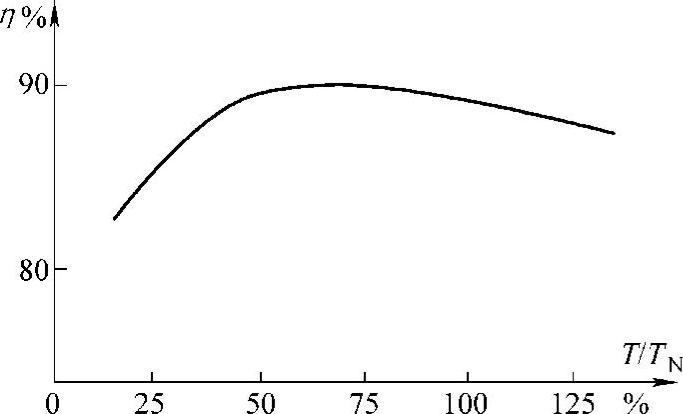
图9-1 电动机效率和负载的关系

由此可见，如果选用的电动机功率过大，出现“大马拉小车”的现象，会导致运行效率下降，无谓地空耗了许多电能。

半导体变流器的效率也是很高的，变流器的损失主要来自于半导体器件导通时的电压降。半导体器件的正向电压降的平均值约为2V，对于桥式电路正向电压降按照4V估算。380～440V电压的变流器的额定损失约为1%，220V的变流器的额定损失约为2%。考虑到无功功率带来的损失，通常认为半导体变流器的效率为0.95～0.98。

机械传动装置，包括减速箱、传动轴等也有机械损失。这种损失主要表现在摩擦损失，这跟齿轮、轴承等机械部件的加工精度以及润滑状况有相当紧密的关系。机械传动装置的效率本质上与传递的转矩值有关，通常是一个变化的数值。

工作机械的整体效率是电气传动的效率与所驱动机械效率的乘积。以风机为例，工作机械总体的效率η_w等于风机效率η_ven和传动装置效率η_drv的乘积，即

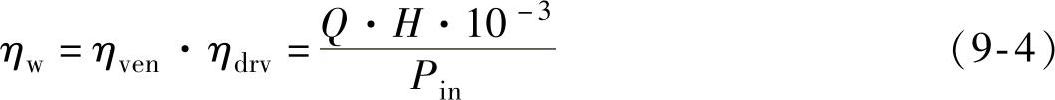
式中 Q——风机输出的流量（m³/s）；

H——风压（Pa）；

P_in——输入的电气功率。

有些工作机械工作在恒定转矩工况，例如提升机、起重机、刨床等，当速度不变时，效率也不变。在一个工作周期中总体效率为

式中 A₁——一个工作周期内的总输入功；

A₂——在一个工作周期内有用功，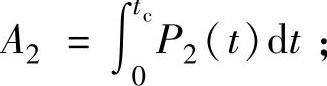

t_c——工作周期；

P₂——有用功率；

ΔA——在一个工作周期内的损失功，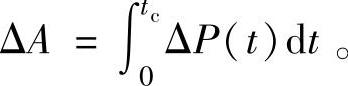

使用交流电源的场合还要考虑流动在电源和用电设备之间的无功功率。无功功率是由励磁功率形成的，其害处是加大电源的电流负荷，增大线路的损耗。评价无功功率的大小的参数是功率因数cosφ，这里的φ角是电压和电流之间的夹角。笼型异步电动机的cosφ为0.70～0.85之间，轻载时功率因数下降。

晶闸管-直流电动机调速系统的无功功率是因相控机理导致电流滞后所引起的，因此cosφ=cosα。因此在高转速时触发角减小，功率因数提高（0.8～0.9）；低速时触发角增大，功率因数降低。

交流电动机和直流电动机都可以采用脉宽调制（PWM）方式来调速，由于采用二极管不控整流器，功率因数可达0.95以上。

许多大功率不调速的工作机械可以采用同步电动机驱动，当同步电动机工作在过励磁状态时，发出容性无功功率，用于补偿电网的感性无功功率。