直流电气传动系统过渡过程分析

本节研究晶闸管—直流电动机电气传动系统的过渡过程。晶闸管整流器被视为一个放大倍数为常数的比例环节。由以下方程来描述恒定励磁的直流电动机的过渡过程（见5.1节）。

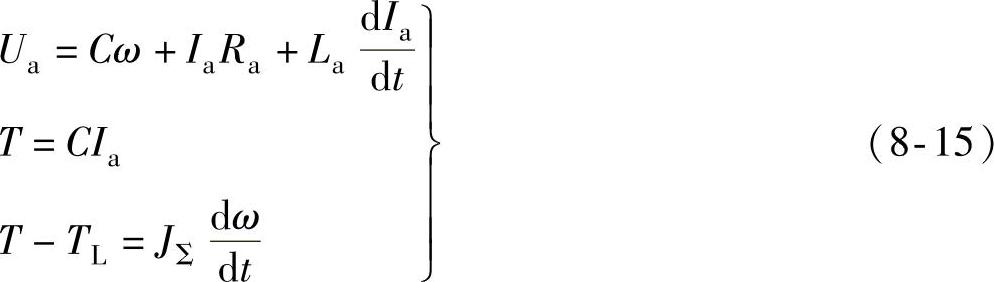
式中 C——磁通不变时的转矩系数，C=C_TΦ。

研究直流电动机的过渡过程需要考虑两个惯性环节，即考虑两个时间常数：机电时间常数τ_m和电枢回路的电磁时间常数τ_a。

由式（8-15）、式（8-16）和式（8-17）得到

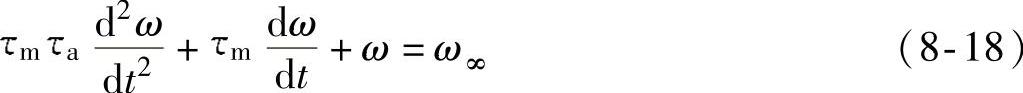
式中 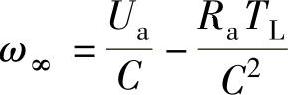——转速的稳态值。

二阶微分方程（8-18）是研究电动机过渡过程的通式。凡是机械特性为线性形式的电动机，都可以用此式描述，区别只在于机械特性的硬度β不同。

用微分算子p=d/dt代替式（8-15）中的微分项，得到如式（8-19）的形式，并可据此绘出电动机的结构框图。

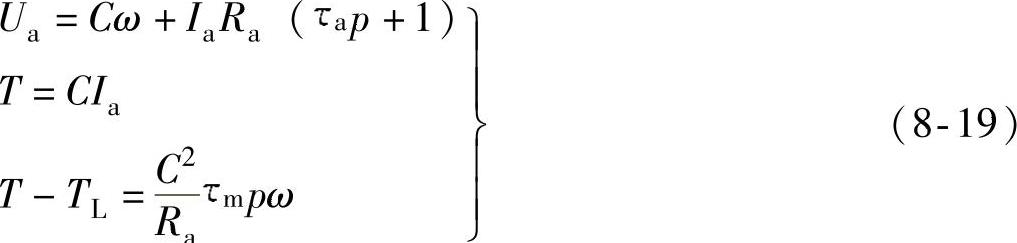
恒定励磁情况下的直流电动机结构框图8-5中由4个典型环节构成：电枢回路——由电枢电压产生电枢电流，惯性环节的时间常数是τ_a；电磁耦合环节——电枢电流在气隙磁通作用下产生电磁转矩，电能转变为机械能，比例环节的系数为C；机械部分——反映了机械部分的转动惯量，惯性环节的时间常数是τ_m；内部反馈环节——电动机内部的旋转电动势，比例环节的系数为C。

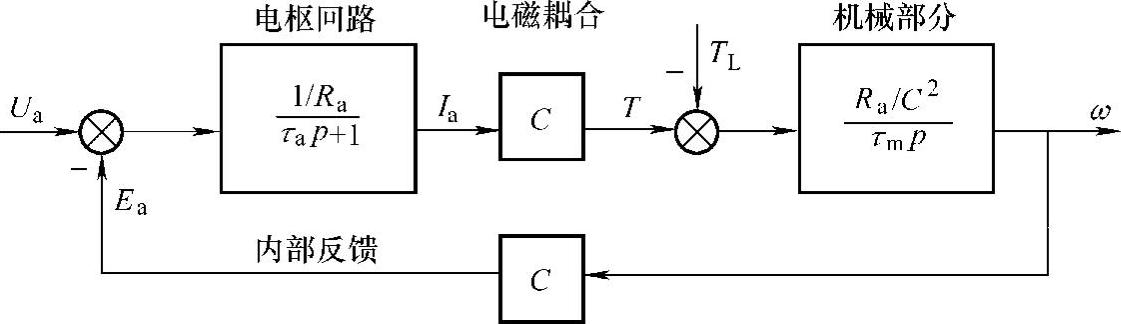
图8-5 恒定励磁的直流电动机的传递函数框图

以电枢电压U_a为输入量，电动机的转速ω为输出量，电动机的传递函数为

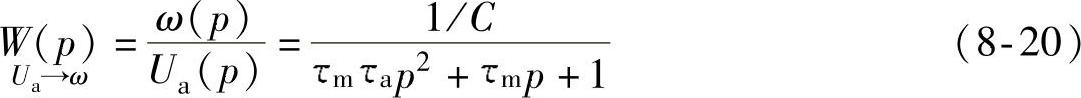
特征方程

的两个根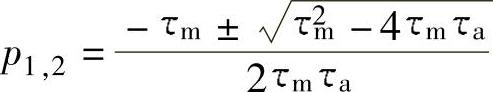决定了过渡过程的特性。

如果τ_m＞4τ_a，两个特征根均为负的实数根，描述转速过渡过程的微分方程（8-18）的解为指数形式，即

在这种情况下，转速的过渡过程呈单调二阶惯性环节的特性（见图8-6）。

如果τ_m＜4τ_e，两个特征根为负实部的共轭复数，p_1，2=α±jΩ，

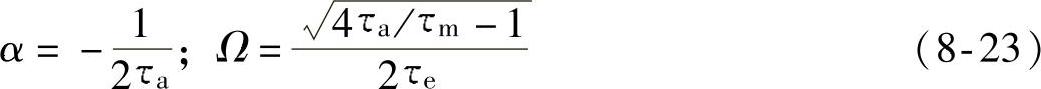
描述转速过渡过程的微分方程（8-18）的解为

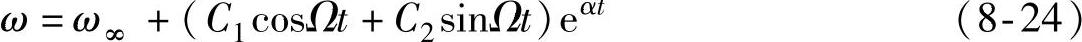
常数C₁和C₂由过渡过程的初始条件和终了条件确定。

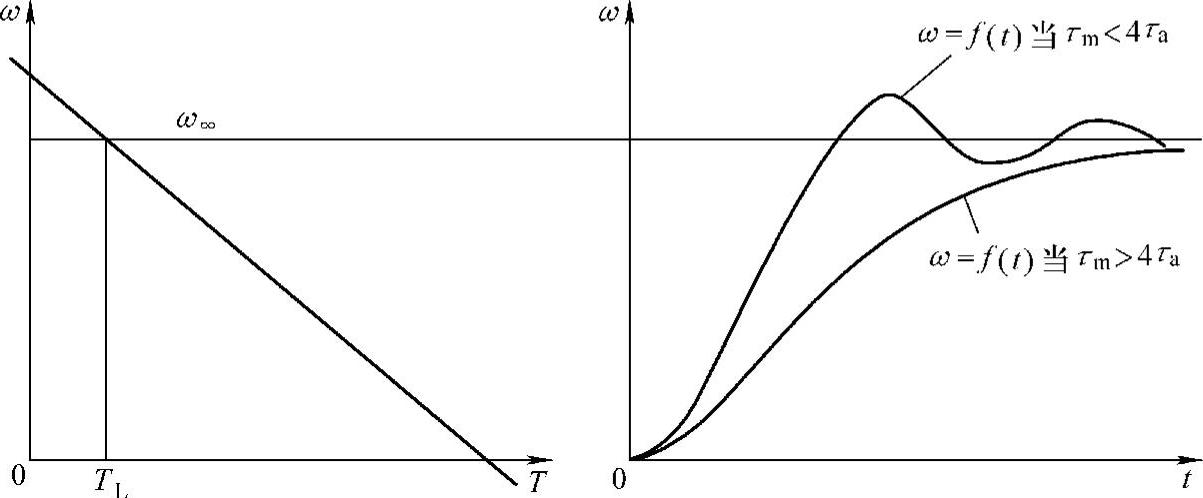
图8-6 具有线性机械特性的电动机在起动时的过渡过程曲线

在这种情况下，过渡过程为指数衰减振荡的形式（见图8-6）。振荡的频率是Ω，过渡过程持续的时间大约是（6～10）τ_a。振荡的本质是电磁能量与动能之间周期性的相互转换。指数衰减的过程只与电磁时间常数τ_a有关。

下面分析电枢电流的过渡过程I_a=f（t）。

由运动方程可以得到

此式说明电枢电流由静态电流和动态电流两部分组成。静态电流和负载成比例，即I_L=T_L/C；动态电流和转速的导数（加速度）成比例。

由结构框图8-5可以得到电动机在输入量为电枢电压U_a，输出量为电枢电流I_a的传递函数

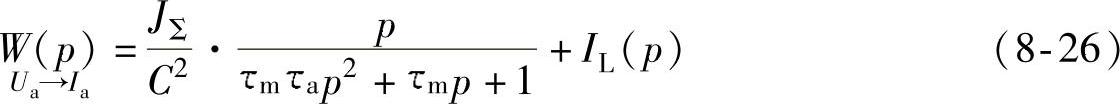
式中 I_L——对应于负载转矩的电枢电流。

图8-7所示为电动机起动并达到稳定速度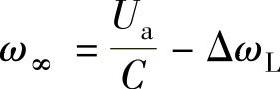时的过渡过程曲线。电动机轴上加有负载转矩T_L。图8-7a是τ_m＞4τ_a情况下的过渡过程曲线；图8-7b是τ_m＜4τ_a情况下的过渡过程曲线。前者的电流和转速都是按指数规律变化的，后者的电流和转速都是按指数振荡规律变化的。从图中还可以看出：在t₀时刻之前，对应于电磁转矩的电枢电流小于负载转矩的电流。虽然电枢电流在增加，但是转速为零；在t₀时刻之后，电磁转矩的电流大于负载转矩对应的电流，电动机开始起动。随着电枢电流增大，电动机开始加速，在旋转电动势的作用下，电枢电流逐渐减小，转速逐渐稳定在稳态值。

下面分析直流电动机在电枢电压不变的条件下，机械负载对过渡过程的影响。图8-5是直流电动机在改变电枢电压进行调速的传递函数框图。现在保持电枢电压不变，考虑负载转矩发生变化对转速的过渡过程带来影响。这种情况的传递函数框图就是把图8-5变换成为如图8-8所示的形式，这时输入量是负载转矩T_L，输出量是转速ω。

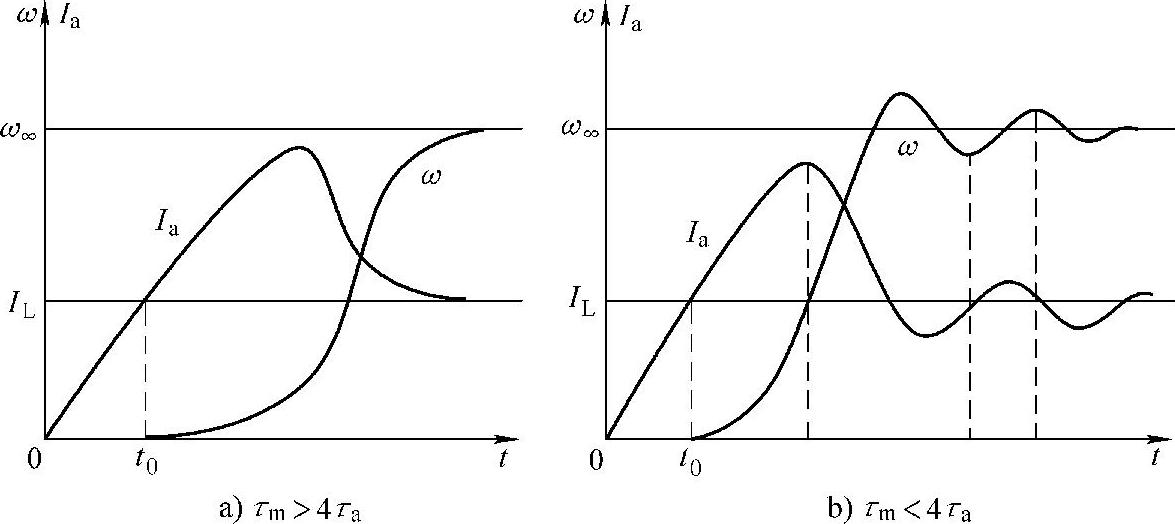
图8-7 电动机起动时电流和转速的过渡过程曲线

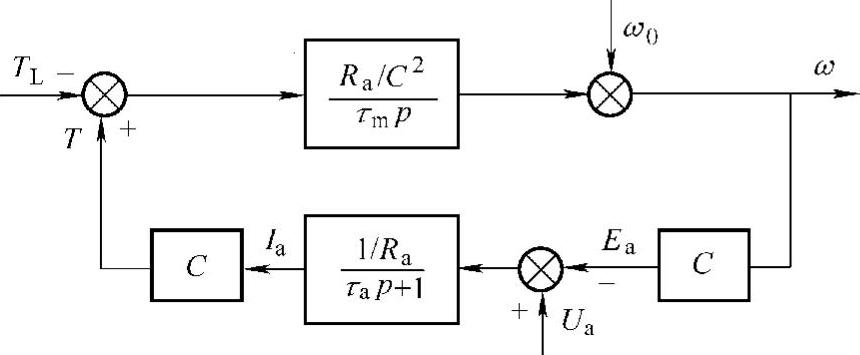
图8-8 恒定励磁的直流电动机在突加负载时的传递函数框图

假设电动机工作在空载状态T_L=0，转速ω₀=U_a/C，电枢电流I_a=0，根据电压平衡方程式有U_a=E_a。

如果在电动机轴上突加负载转矩T_L=CI_L，则电动机的转速开始下降，电动势也将减小，电枢电流则开始增加（见图8-9）。

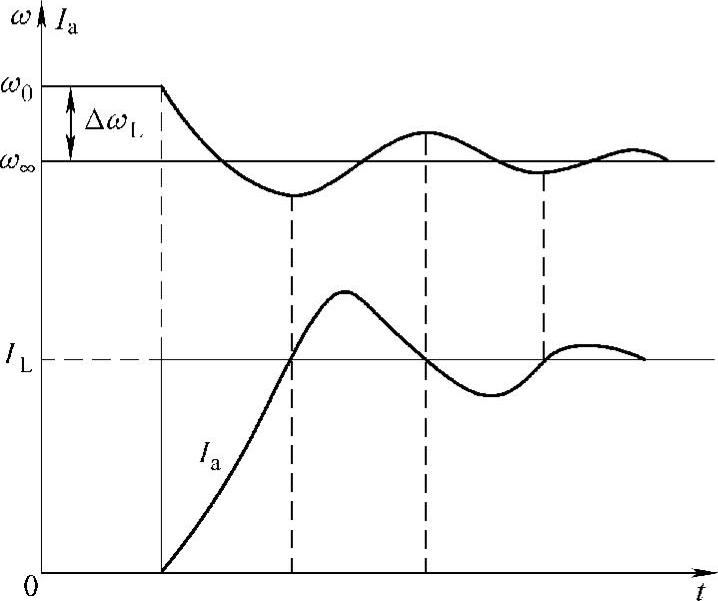
图8-9 突加负载时直流电动机的 电流和转速的过渡过程

如果电枢的电感足够大，满足条件τ_m＜4τ_a，电枢电流上升的速率小于转速下降的速率。当转速开始小于新的稳态值ω_∞=ω₀-Δω_L=ω₀-T_L/β时，电流还没有达到对应于转矩T_L的稳态值I_L，所以转速将继续下降。当电枢电流继续增大到I_L后，转速开始上升，经过几次振荡后，电流和转速达到稳定值。需要注意的是：曲线ω=f（t）和I_a=f（t）具有相关性，电流（或转矩）是转速的一阶导数，当转速ω在最大值和最小值的时刻，即dω/dt=0的时刻，正好对应着电流I_a穿过负载电流I_L的时刻。

如果电枢的电感不满足条件τ_m＜4τ_a，突加负载的过渡过程是一个单调变化的过程。当电枢电压恒定U_a时，把负载变化作为转速的扰动作用，其传递函数为(www.xing528.com)

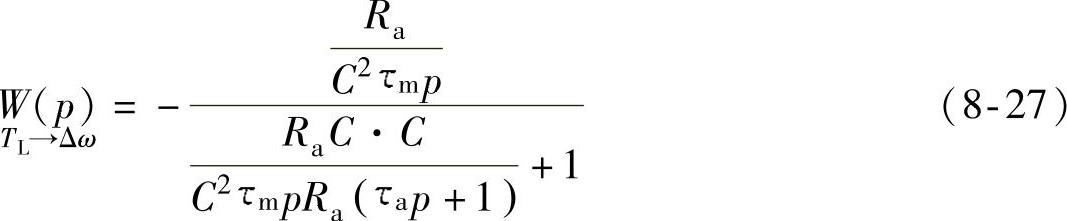
经过化简后得到

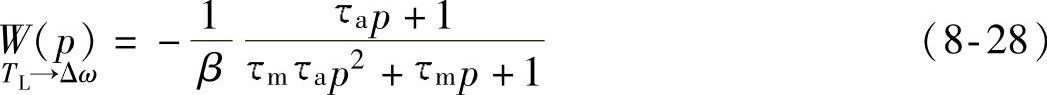
式中 β——电动机机械特性的硬度，β=C²/R_a。

传递函数公式（8-28）表明，电动机轴上突然加上负载转矩T_L，经过过渡过程之后将会产生稳态速降Δω_L，令微分算子p=0，可以得到

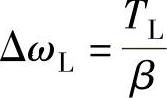
即稳态速降值与负载转矩成正比，与机械特性的硬度成反比。对于闭环控制的电气传动系统，β是指闭环后的机械特性硬度。

众所周知，采用速度闭环的控制系统可以提高速度调节的精度。带有速度闭环的晶闸管-直流电动机调速系统的传递函数框图如图8-10所示。速度调节器为放大倍数为k_s的比例环节，晶闸管装置等效为放大倍数为k_SCR的比例环节，速度反馈系数为k_α。

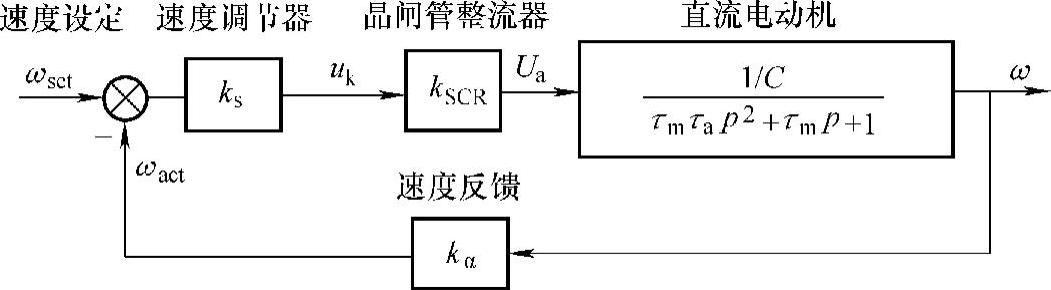
图8-10 晶闸管-直流电动机调速系统的传递函数

由图8-10可以得到速度闭环的传递函数

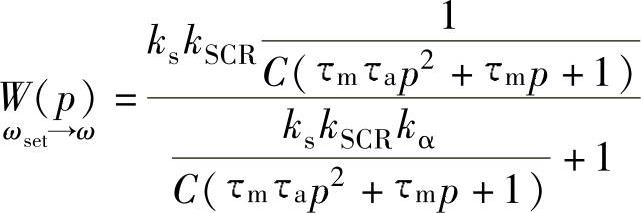
令闭环放大倍数K=（k_sk_SCRk_α）/C，上式可以简化为

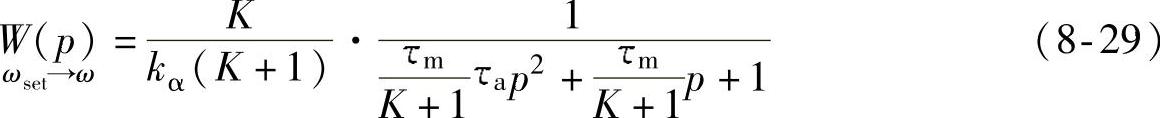
式（8-29）的传递函数表明，在速度闭环的电气传动系统中，代表机械惯性大小的机电时间常数τ_m减小为原值的1/(K+1)。闭环控制后传动系统的机械特性硬度β增大为原来值的(K+1)倍（见式（4-8））。速度闭环控制的优点是提高了响应速度，而缺点是增强了过渡过程振荡特性。

通常电动机的机电时间常数τ_m＞4τ_a，在开环控制的情况下过渡过程不会出现振荡现象。在实施速度闭环控制的情况下，等效的机电时间常数减小，而且很多时候闭环放大倍数K都很很大，等效时间常数往往小于4倍的τ_a，这就是过渡过程出现振荡的原因。为了抑制闭环控制所带来的振荡特性，需要在控制系统中加入校正环节，使过渡过程的指标达到要求。

如果描述系统的数学模型是线性（或者是经过线性化处理）的微分方程，一般采用如下的步骤分析其过渡过程：

（1）确认惯性环节的类型和数量；

（2）求出各个惯性环节的时间常数；在工程计算时可以把相差2个数量级以上的小时间常数忽略；

（3）惯性环节的数量就是描述过渡过程微分方程的阶数；

（4）列出特征方程（令微分方程的左侧部分等于零），并求出特征根；

（5）用单位阶跃给定函数或者单位阶跃扰动作为激励，求出响应的函数式y=f（t），y表示电气传动系统中的参数，一般指电流、转矩和速度。

例题8.2分析晶闸管—直流电动机调速系统的开环和闭环的过渡过程特性。

直流电动机的基本数据：额定电枢电压U_N=220V，电枢电阻R_a=0.6Ω，电枢电感L_a=0.02H，电动机转矩常数C=1.9V·s，额定转速ω_N=104.7rad/s（即n_N=1000r/min），转动惯量JΣ=1.0kg·m²。系统的速度给定值ω_set为0～10V，晶闸管整流器的控制电压u_k为0～30V，整流器输出电压U_a为0～300V，速度反馈系数k_α=0.09V·s。

解1.电枢回路的电磁时间常数

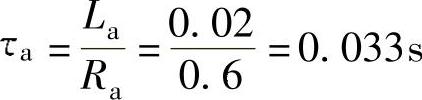
2.机电时间常数

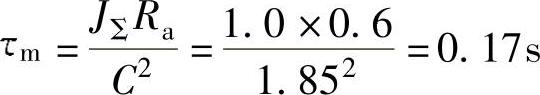
3.开环时速度调节器的放大倍数

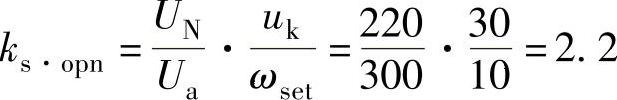
4.当晶闸管整流器的输出电压为220V时，其输入电压u_k为

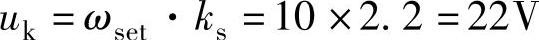
5.晶闸管整流器的放大倍数

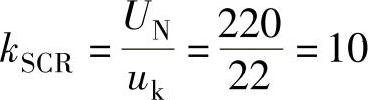
6.闭环后晶闸管整流器的输入电压为

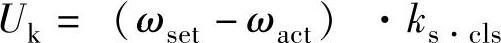
则闭环时速度调节器的放大倍数

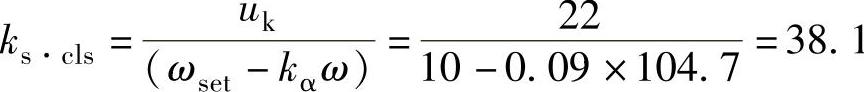
7.总的闭环放大倍数

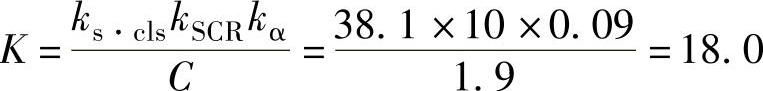
8.闭环时等效的机电时间常数

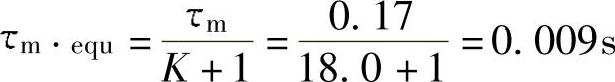
9.开环时

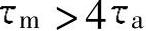即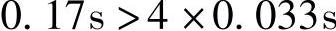

这说明在开环控制时，过渡过程呈单调非振荡特性。

10.闭环时

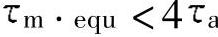即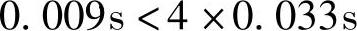

这说明在闭环控制时，过渡过程呈衰减振荡特性。