阶跃响应特性及强励系数优化

所谓电气传动系统的过渡过程是指电动机在起动、停止、加减速、加减负载等动态过程。在这个过程中，电流、转矩、速度等物理量随时间变化，并由一个稳态值变化到另一个稳态值。这种变化是不可能瞬间完成的，电流受到电磁参数的制约不能瞬变，速度受到机械惯量的制约也不能瞬变。

产生过渡过程的原因不外乎以下两种：

-控制原因：通过控制改变电气传动系统的运行状态，例如人为改变电动机的速度；

-扰动原因：外界扰动因素使得电气传动系统的状态发生变化，例如电动机轴上负载的变化。

许多生产机械，如轧钢机、挖掘机、数控机床等必须具有优良的动态特性，具有快速地改变速度的能力，或者对变化的负载特性做出尽快的响应。只有当电气传动系统具有较大的功率储备，才能缩短过渡过程的时间，减小过渡过程的波动。

有些生产机械，如造纸机、胶片机等需要速度稳定。一般情况下速度的设定值都是稳定的常数值，外界的扰动是影响速度稳定的主要因素。对于这类机械的传动系统，应当通过改善调节系统的特性，以使扰动引起的速度偏差值最小。

对于驱动随动系统的伺服电动机，速度和位置的控制精度十分严格。过渡过程的特性就显得更加重要。

图8-1所示为阶跃给定时的过渡过程曲线，又称飞升曲线。过渡过程可以简单地分为振荡过程（曲线1）和单调过程（曲线2）两种类型。图中还给出描述过渡过程品质的几个指标：

上升时间t_r：被调节量y（t）第一次达到其稳态值y（∞）的时间，表示消除偏差的速度。它是反映过渡过程快速性的一个指标。

过渡时间t_s当t≥t_s时，满足

t_s是指被调节量y（t）开始进入并驻留于±δ%的邻域内的时间。式中的δ%为指定小数，通常取值2%或5%。显然，过渡时间t_s也是描述过渡过程快速性的指标，它代表了系统跟随给定值或在扰动后恢复原值的快慢程度。

超调量σ_p：代表被调节量的过冲程度，即反映了系统的稳定性。可以把超调量定义为是指被调节量y（t）和稳态值y（∞）之偏差与稳态值y（∞）的最大相对值，即

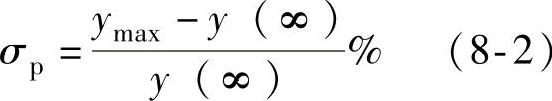
超调量越大，系统的稳定性就越差，反之亦然。

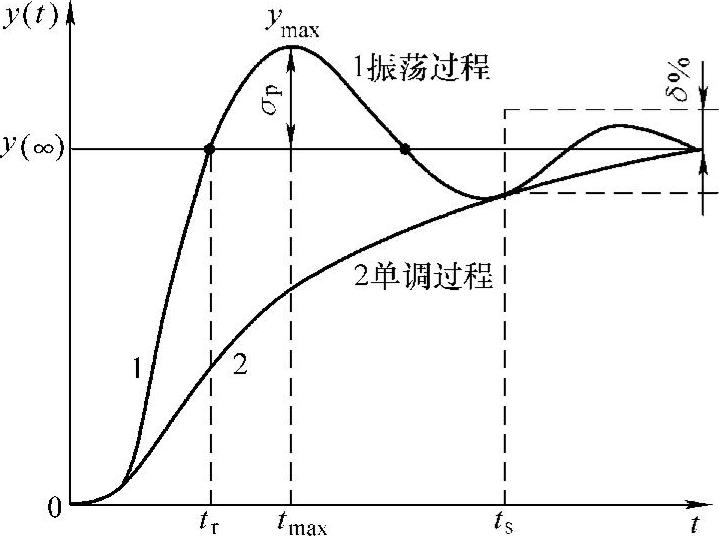
图8-1 阶跃给定时过渡过程曲线

静差：指过渡过程结束后尚剩余的偏差。对于恒值系统来说，是指在扰动的作用下，最后偏离原稳定值的大小；对于随动系统来说，是指偏离给定值的大小。静差代表静态特性的好坏，又称为稳态精度。

以上这些描述过渡过程品质的指标都是在单位阶跃给定或者单位阶跃扰动的基础上得到的。

为了计算和分析过渡过程的特性，必须建立过渡过程的方程式，即电气传动中各种物理量（如速度、电流、转矩等）与时间的函数关系。这些函数关系通常都是用微分方程来表示的，而微分方程的阶数是由系统中所包含惯性元件的数量所决定。下面叙述电气传动系统中的主要惯性元件。

机械的惯性与储存动能的元件有关；度量转动物体的机械惯性的物理量是转动惯量，其量值取决于物体的形状、质量分布及转轴的位置。对于常规的电气传动系统，我们所关注的是把相关转动物体（电动机和工作机械）的转动惯量折算到同一轴上，即总的转动惯量JΣ。在分析电气传动系统的过渡过程时，转动惯量以机电时间常数τ_m的形式出现，即

式中 β——电气传动系统的机械特性的硬度。

电磁惯性与储存电磁能量的元件有关；量度电磁惯性的参数是电磁时间常数τ_e，(www.xing528.com)

式中，L和R分别是电磁储能元件（例如线圈）的电感值和电阻值。

静电惯性与储存静电的电容器有关；度量这个惯性的参数是静电时间常数τ_c，

τ_c=RC （8-5）

式中 C——电容量；

R——充放电回路的电阻值。

机械惯性、电磁惯性、静电惯性都是各种储能元件的本质属性，这些时间常数在以后研究过渡过程时也会经常用到。

只要系统中有储能元件，能量的储存和释放不能瞬间完成，就会存在惯性，从一种运动状态过渡到另一种运动状态就不能瞬间完成。时间常数就是描述这种过渡过程特性的重要参数。

如果能流的方向是单方向的，则过渡过程也是单调的曲线。例如接通直流电动机的励磁回路的电压，励磁电流随时间变化的过程就是单调上升的曲线（见图8-2）。可以用微分方程来描述这个电流的变化过程

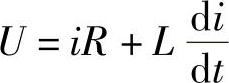
考虑到电磁时间常数，得到

式中 I_∞——励磁电流的稳态值。

用微分算子代替p微分符号d/dt，得到

i（τ_ep+1）=I_∞

解此微分方程得到

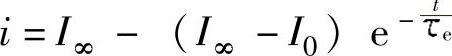
式中 I₀——励磁电流的初始值。

当I₀=0时，上式可以简化成为

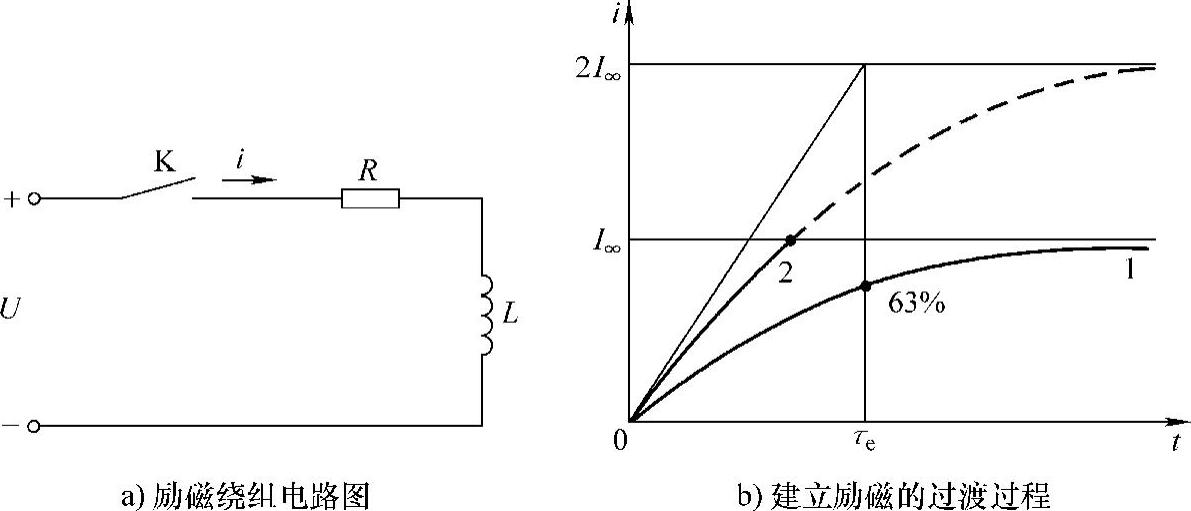
图8-2 接通励磁绕组开关时励磁电流的过渡过程

励磁电流的过渡过程i=f（t）是一个指数特性的曲线（见图8-2b）。对应于τ_e时刻，电流增大到0.63I_∞，在3τ_e时，电流增大到0.95I_∞，在5τ_e时，电流增大到0.996I_∞。实际工作中，可以近似认为过渡过程的时间是（3～5）τ_e。若要缩短电流的过渡时间，唯一的办法就是增大励磁绕组的电压，也就是常说的强励作用。例如可以把励磁电压增大一倍，这时励磁电流的过渡过程是曲线2，电流的稳态值是2I_∞。当励磁电流达到I_∞时，再把励磁电压减小到正常值。很明显，强励作用加快了过渡过程。工程中强励系数一般取2～3倍。