异步电动机机械特性优化：全面解析

先来研究绕线转子异步电动机转子短接的工作情况。式（3-4）表明，异步电动机的电磁转矩同磁通Φ、转子有功电流分量I₂′_a成比例（撇号表示把转子侧的电流值折算到定子侧）。磁通Φ是电源电压通过定子绕组产生的，它的值同电源电压的有效值U₁和频率ω₀有关，即

转子电流I₂为

式中 Z₂——转子相绕组的全部阻抗。

转子绕组的感抗x₂的值随转子电流频率变化，也可以说x₂随转差率s变化，即

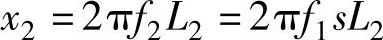
在转子静止时（s=1），转子绕组的感抗x₂最大；随着转速升高（s减小），x₂逐渐变小；当转速达到额定值，x₂约为s=1时的最大值的1%～3%。把s=1时的x₂定义为额定值，表示为x₂·s=1=x_2N，于是有

x₂=x_2N·s（3-12）然后得到转子电流为

转子电流的有功分量为

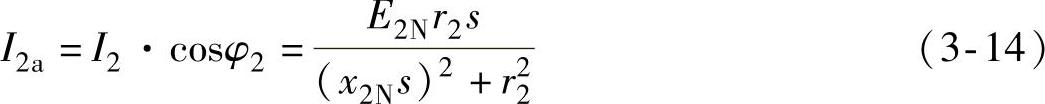
式中

根据功率不变性原理，可以把转子回路的参数折算到定子侧，并考虑到电动机的电压比k_T=U₁/E_2N，则折算公式为

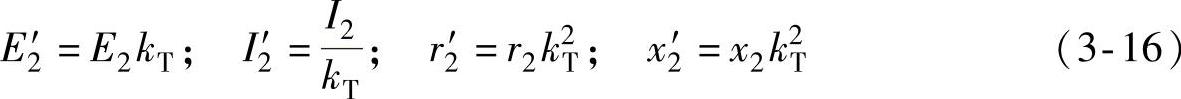
继而由式（3-16）得到

和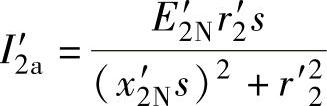 （3-17）

把式（3-17）的分子、分母同除以s，得到

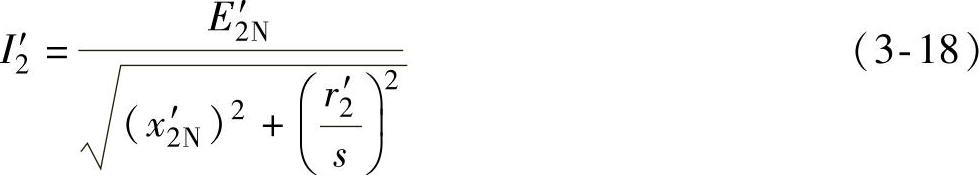
这种分子分母同时除以s只是一种数学运算，并不影响公式（3-18）的有效性。实际上在最初的公式（3-13）中已经清楚地表明，转子感抗x₂与转差率有关，转子电阻r₂是个常数，与转差率无关。根据式（3-18）可以绘出异步电动机的一相的等效电路，如图3-3a所示。异步电动机的矢量图如图3-4所示。

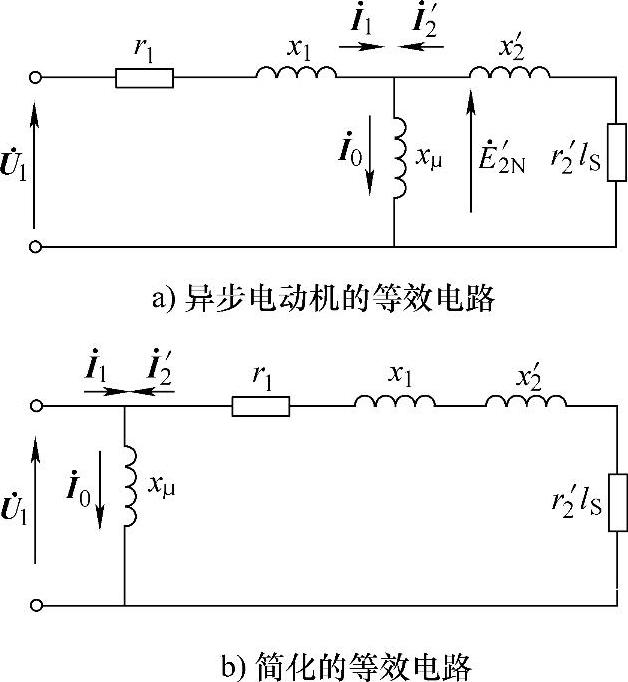
图3-3 异步电动机的等效电路图

图3-4 异步电动机的矢量图

为了简化分析，可以把等效电路中的励磁支路移到进线侧。简化的等效电路如图3-3b所示。由简化的等效电路可以得到转子电流

式中 x_k——定子回路和转子回路的总感抗，x_k=x₁+x′_2N。转子电流的有功分量为

把式（3-10）和式（3-20）代入式（3-4），就可以得到异步电动机转矩的公式

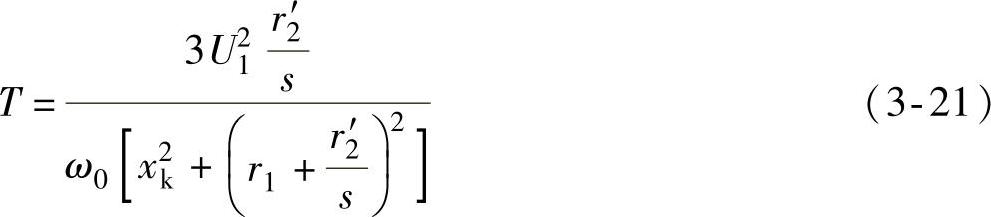
这个公式也可以表示为异步电动机的机械特性s=f（T）。异步电动机的机械特性如图3-5所示。图中还绘有反映异步电动机的机电特性s=f（I₁）的曲线。(www.xing528.com)

图3-5 异步电动机的机械特性和机电特性

把励磁电流视为电流的无功分量，并由相量图3-4可得到

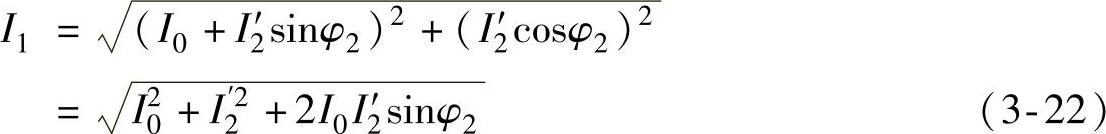
式中

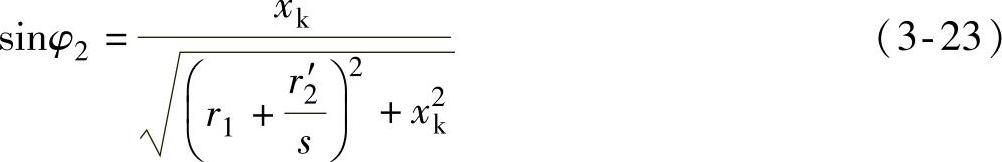
在图3-5机械特性中转矩拐点的值叫做临界转矩T_k，它是机械特性中转矩的最大值，负载转矩不可超过该值。如果负载转矩超过临界转矩值，将导致电动机堵转。临界转矩相对应的转差率叫作临界转差率s_k。在式（3-21）中对s求导，并令dT/ds=0，可以得到临界转矩和临界转差率：

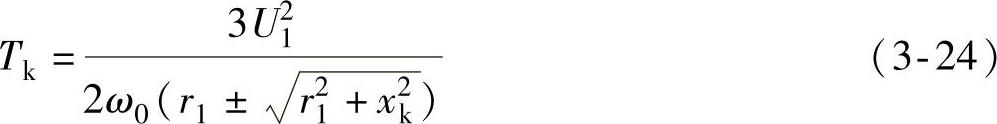
临界转差率s_k的符号取正号，表示电动机工作在电动工况；取负号，表示电动机工作在发电工况。临界转矩和额定转矩的比值叫做异步电动机的过载倍数λ

根据式（3-24）和式（3-25）可以把机械特性公式（3-21）转换为更便于使用的形式

如果异步电动机的功率大于15kW，并且工作电源的频率是50Hz，那么定子电阻r₁远小于定子回路的总电抗x_k，因此可以忽略r₁，可以把式（3-24）、式（3-25）简化，得到

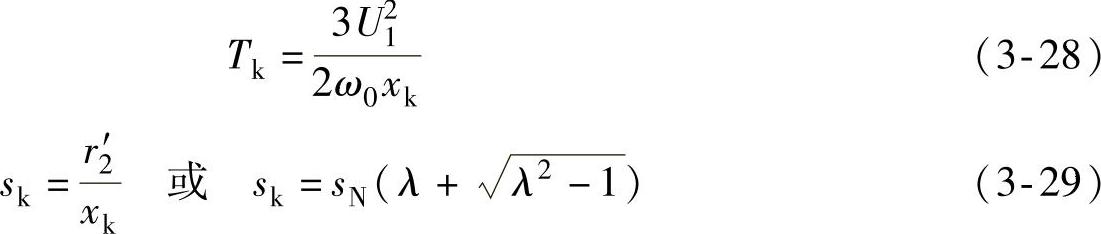
于是机械特性公式（3-27）可以简化成为实用机械特性表达式

有了式（3-27）和式（3-30），就可以根据电动机的铭牌数据及其导出数据——额定转差率s_N、额定转矩T_N和过载倍数λ计算出该电动机的机械特性。

异步电动机机械特性（图3-5）是非线性的，由两个区段组成。第一个区段是对应于转差率从0到s_k的区间，这个区段是工作区段。第二个区段是在转差率大于临界转差率（s＞s_k）的曲线，这个区段的特性适用于电动机的起动，所以叫做起动区段。

因为在工作区段的转差率很小，几乎没有趋肤效应的影响，计算的结果相当准确。而计算起动区段的机械特性是一个复杂的过程，而我们更关心的是具有代表性的几个特征点。可以用四个具有代表性的特征点近似描述异步电动机的机械特性：同步转速点（s=0），最大转矩点（T=T_k），起动转矩点（s=1）和最小转矩点（T=T_min）。在电动机的产品样本和电动机手册中可以查到这些特征点的数据。

工作区段机械特性近似线性，斜率基本恒定并且为负值。转矩同定子电流I₁和转子电流I₂成正比。由于在工作区段中总是有s＜s_k，式（3-30）中分母的第二项很小，可以忽略不计。于是工作区段的机械特性可以写成线性形式

起动区段的硬度β为正值。尽管电动机的电流增加，转速却降低（转差率增加），转矩也减小。如果将绕线转子异步电动机的转子绕组短接，起动时（ω=0，s=1）电流就会很大，甚至达到额定电流的10～12倍，而起动转矩却只有额定转矩的0.4～0.5倍；笼型异步电动机的起动电流是额定电流的5～7倍，起动转矩是额定转矩的0.9～1.3倍。

为了解释起动电流和起动转矩不协调的现象，可利用转子回路的相量图（图3-6）予以解释。这里分为两种情况：转差率较大的起动区段（见图3-6a）和转差率较小的工作区段（见图3-6b）。

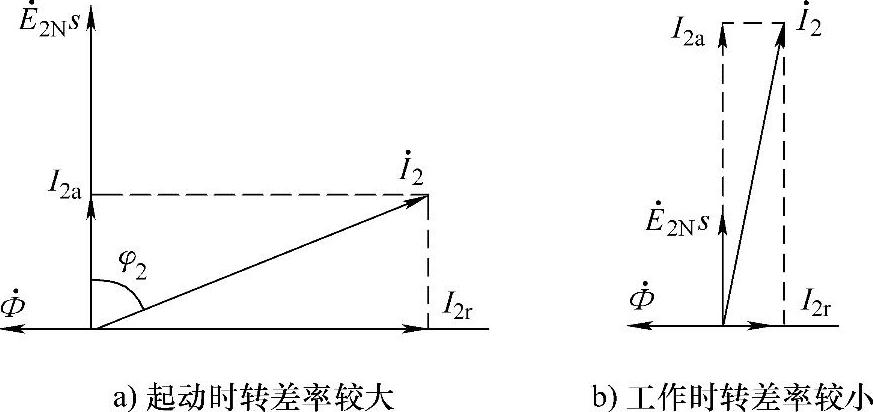
图3-6 异步电动机转子回路的相量图

起动时s=1，转子电流的频率等于电源频率f₂=50Hz。转子绕组的感抗x₂很大（见式（3-12）），大大超过转子绕组的电阻r₂，转子电流滞后电动势的角度φ₂很大，即转子电流主要是无功分量。由于这时的电动势E_2.s=1=E_2N是最大值，起动电流自然会很大；而转子回路的功率因数cosφ₂却很小，即转子电流的有功分量很小，发出的电磁转矩自然也很小。

随着电动机加速，转差率减小，转子的电动势、频率、感抗都成比例减小，相应地转子电流和定子电流也会减小。尽管如此，由于这时cosφ₂增大，即转子电流和定子电流的有功分量增大，电磁转矩自然就会增大。

随着电动机继续加速，转差率变成小于s_k，进入机械特性的工作区段。这时转子电流的频率相当低，致使转子绕组的感抗也非常小，转子电流几乎都是有功分量（见图3-6b），电磁转矩和正比于转子电流。如果电动机的额定转差率s_N=2%，相当于起动时转差率的1/50。所以在额定工作状态，转子感抗、转子电动势都是起动时的1/50。当电动机带有额定负载时，足以使转子电流达到额定值，转矩也达到额定值。严格说来，异步电动机的机械特性取决于转子绕组的感抗值，而这个感抗值与转差率成正比。