模糊控制系统基本概念与实现方法

1.模糊控制理论基础

（1）模糊控制的有关术语

表5-46是模糊控制的有关术语。

表5-46 模糊控制的有关术语

（2）隶属函数和模糊集

设A是论域U上的一个集合，对任意的u∈E，令

则称C_A（u）是集合A的特征函数。

任意一个特征函数都唯一确定一个子集A={u|C_A（u）=1}，任意一个集合A都有唯一确定的一个特征函数与之对应。因此，集合A与其特征函数C_A（u）是等价的。

特征函数C_A（u）在u₀处的值称为u₀对集合A的隶属程度，简称隶属度。当u∈A时，隶属度为100%（即1），表示u绝对属于集合A；当u/∈A时，隶属度为0%（即0），表示u绝对不属于集合A。

经典集合论的特征函数只允许取{0，1}两个值，与二值逻辑对应，模糊数学将特征函数推广到可取闭区间[0，1]的无穷多个值的连续值逻辑，即隶属函数μ（x）满足

0≤μ（x）≤1 （5-46）

或表示为：μ（x）∈[0，1]。

给定论域U上的一个模糊子集A，是指对于任意u∈U，都指定了函数μ_A，μ_A（u）∈[0，1]的一个值。

A={u|μ_A（u）}∀u∈U （5-47）

称论域上的一个模糊子集，简称模糊集。其中，μ_A是模糊子集A的隶属函数（Membership Function）。μ_A（u）是u对模糊子集的隶属度。当μ_A值域取值[0，1]的两个端点时，μ_A就是特征函数，A就是普通集合，因此，普通集合是模糊集合的特殊情况。常用隶属函数见表5-47。

表5-47 常用隶属函数

（3）模糊集运算

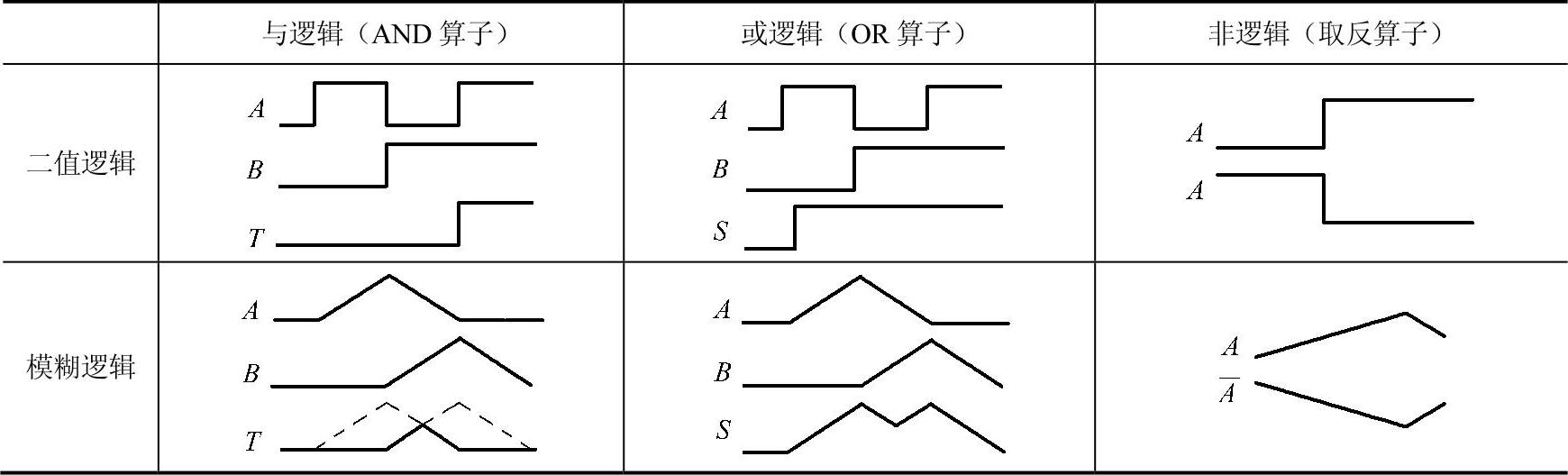
模糊集与普通集合一样，可以进行与、或和非逻辑的运算。由于模糊集用隶属函数描述其特征，因此，它们的运算是逐点对隶属度进行相应的运算。

1）与运算：模糊集A与模糊集B的与运算是它们的交集T。

T=A∩B，其隶属度函数为μ_T（u）=min[μ_A（u），μ_B（u）]，或表示为T（μ_A（u），μ_B（u））。

2）或运算：模糊集A与模糊集B的或运算是它们的并集S。

S=A∪B，其隶属度函为μ_S（u）=max[μ_A（u），μ_B（u）]，或表示为S（μ_A（u），μ_B（u））。

3）非运算：模糊集A的非运算是它的补集C。C=A，其隶属度函数为μ_C（u）=1-μ_A（u）。

与、或和非逻辑运算的比较见表5-48。其他逻辑运算关系有：有界差、有界和、有界积、蕴涵、等价等，可参考有关资料。

表5-48 与、或和非逻辑运算的比较

（4）模糊控制器基本结构

图5-44是模糊控制器的结构框图。模糊控制器由模糊化、知识库、模糊推理和解模糊化等部分组成。

图5-44 模糊控制系统的基本结构框图

1）模糊化：用于将输入的精确量（包括系统设定、输出、状态输入信号）转化为模糊量。例如，通常将输入的测量信号按偏差和偏差变化率进行模糊化。

2）知识库：由数据库和模糊控制规则库组成，用于存放各语言变量隶属度函数等和一系列控制规则。

3）模糊推理：根据模糊逻辑进行推理。

4）解模糊化：也称为清晰化。它将模糊推理得到的模糊输出量转化为实际的清晰控制量。

2.模糊控制语言

模糊控制语言（Fuzzy Control Language，FCL）是模糊控制编程语言，它用模糊控制功能块实现。

（1）模糊控制功能块

模糊控制功能块的声明格式与一般功能块类似，其格式如下：

FUNCTION_BLOCK 模糊控制功能块名

输入变量声明段；

输出变量声明段；

其他变量声明段；

模糊化声明段；

清晰化声明段；

规则块声明段；

可选参数声明段；

END_FUNCTION_BLOCK

（2）模糊化

模糊化用于将输入变量的清晰值转变为模糊量，模糊化声明段的格式如下：

FUZZIFY变量名

TERM 语言项名：=隶属度函数；

END_FUZZIFY

模糊化时应注意下列事项：

1）变量名是在模糊控制功能块中输入变量声明段已经声明需要模糊化的变量名。

2）语言项名用TERM关键字引导，例如，Cold项、Warm项等。

3）隶属度函数描述该模糊变量的清晰量的隶属度，通常采用分段线性函数，例如，三角形或梯形隶属度函数。

4）隶属度函数用多个点的列表定义。其隶属度函数格式如下：

点1，点2，…

其中，点1，点2等是一个数对，其间用逗号分隔，每个数对用圆括号括起来，它们按升序排列，例如，（15.0，0.0），（20.0，1.0），（25.0，0.0）等。相邻两点之间约定为直线。点的个数至少两点，最多个数由相符性等级规定。

5）隶属度函数的基点可通过调整功能块输入变量实现。这些变量必须在功能块输入变量声明段声明。

6）隶属度确定规则如下：

①小于第一点的全部输入变量值的隶属度与第一点的隶属度值相同。

②两个点之间的输入变量的隶属度通过相邻隶属度函数点之间的线性插值计算。

③大于最后点的全部输入变量值的隶属度与最后点的隶属度值相同。

【例5-3】模糊化示例。

图5-45是用图形描述的Temp变量的隶属度。

(www.xing528.com)

图5-45 隶属度的图形描述

（3）清晰化

清晰化也称为去模糊化。它是模糊化的逆过程。输出变量的推理结果必须经清晰化转变为清晰值。清晰化声明段的格式如下：

清晰化时的注意事项如下：

1）变量名是在模糊控制功能块中输出变量声明段已经声明需要清晰化的变量名。

2）RANGE表示输出变量隶属函数的范围。min和max是其下限和上限，它们之间用两个点“..”分隔。如果未定义其范围，则采用该变量数据类型的约定范围。

3）语言项名与模糊化时的定义方法相同，通常，采用单点集定义输出隶属函数。当采用单点集表示输出时，RANGE项不起作用。例如，TERMClosed：=0；是单点，只表示输出为0时，隶属函数值为1。

4）清晰化的方法用语言元素METHOD定义，有重心法（CoG或CoGS）、面积中心法（CoA）、左取大法（LM）和右取大法（RM）四种。例如，METHOD： CoG；表示用重心法进行清晰化。

表5-49是清晰化方法的计算公式。图5-46是LM和RM的区别。

表5-49 模糊控制的清晰化方法

注：U是清晰化结果；u是输入变量；p是单点集的个数；是模糊集综合后的隶属函数；i是下标；min和max是RANGE定义的变量的最小值和最大值，对单点集，min=-，max=+；sup是最大值，inf是最小值。

5）约定值项是当输出变量所有语言项的隶属度都为零时，为生成有效的输出，所规定的一个默认值。当输出变量没有规则被激活时，采用约定值项的值。约定值可由用户直接规定，例如，DEFAULT：=0.0；表示约定值为0.0。也可用约定值NC表示保持上一步推理结果的输出。

图5-46 LM和RM的区别

6）隶属度函数可以是单点集，也可以是点。单点集用数值文字或变量名描述。点用数值文字、变量名、逗号和数值文字表示。

（4）规则块

规则块用于存放各语言变量隶属度函数等和一系列控制规则，也称为知识库。规则块声明格式如下：

编写规则块的注意事项如下：

1）运算符（Operator）有AND和OR。根据摩根定律，运算符AND和OR是对偶的，例如，MIN用于AND，则MAX用于OR。表5-50是AND和OR的对偶算法。

表5-50 AND和OR的对偶算法

运算符（算子）定义的格式如下：

算子：算法关键字；

例如，AND：PROD表示采用AND运算符，其算法是乘积PROD。

2）激活方法（Activation method）是可选项。其格式如下：

ACT：可选的激活方法；

可选用的激活方法有直积（PROD）和取小（MIN）两种运算，即两个输入变量的直积或最小运算结果作为激活方法。激活方法与是否用单点集输出无关。如果无激活方法，则不列写该声明段。

3）综合方法（Accumulation method）用于定义两个输入变量之间的关系。其声明的格式如下：

ACCU：综合方法；

表5-51是可选的综合方法，共有MAX、BSUM和NSUM三种。

表5-51 可选的综合方法

4）规则号由RULE和流水号组成，例如，RULE1表示规则1等。

5）语言规则是以IF关键字开始，紧跟条件，条件后是THEN关键字和结论，最后是分号表示的规则。条件是用各子条件用运算符AND、OR、NOT等逻辑组合的。运算符的优先级，从高到低依次是圆括号、NOT、AND和OR。

6）子条件可以是语言变量，或以语言变量开始，后面是关键字IS、可选的NOT和条件中用到的语言变量的一个语言项。例如，TEMPISWARM表示温度变量（TEMP）是暖（WARM）的子条件。当NOT用于子条件之前时，可用圆括号将该子条件括起来，例如，IF NOT（TEMP IS HOT）THEN…。

7）结论可分为几个子结论和输出变量，各子结论之间用逗号分隔。子结论以语言变量开始，后面是关键字IS及该语言变量的一个语言项，例如，VALVE1 IS OPEN，PUMP1 IS RUN等。

8）加权因子描述控制规则的重要程度、可信程度和置信程度，其值是在0～1之间的一个数，用关键字WITH后跟加权因子表示。例如，Valve_2 IS Inlet WITH0.7；表示阀Valve_2是0.7开度的进口阀。

（5）可选参数

为在不同目标系统实现模糊控制的应用，需要附加信息，以获得不同系统间的最佳转换，可选参数声明段的格式如下：

OPTIONS

制造商规定的附加参数；

END_OPTIONS

（6）模糊推理

模糊推理（Fuzzy Inference）是根据模糊推理机制，按规则和所给事实执行推理过程，获得有效结论。

基本模糊推理系统有三类，它们的差别是模糊规则后件不同。

1）Tsukamoto模糊模型。它将系统的总输出表达为每条规则精确输出的加权平均，而每个规则的精确输出由前件激励程度（用PROD和MIN算子计算）和后件的隶属度函数确定。后件的隶属度函数通常是单调函数。

2）Mamdani模糊模型。系统的总输出通过MAX算子将全部规则的有效后件集合而成。即每条规则有效输出由前件激励程度和后件隶属度函数共同确定。清晰化的方法有CoA、CoG等。是最常用的模糊推理方法。

3）Takagi-Sugeno模糊模型。每条规则输出是输入变量的线性组合加常数项，因此，总的输出是每条规则的加权平均。

根据Mamdani推理方法，可将推理过程分为三部分：聚集、激活和综合。

1）聚集：用于确定规则中条件的满足程度。从一条规则前件的子条件隶属函数来确定前件条件的满足程度。如果条件只有一个子条件，则条件的满足长度就是该子条件的满足程度。如果条件有几个子条件，则条件的满足程度是各子条件满足程度通过聚集来确定。子条件是AND组合的，则满足程度用AND算子计算。

2）激活：即匹配，用于确定规则中结论的满足程度。当前件的满足程度（隶属函数的值）大于1，则该规则被激活。对所有n条规则，根据IF条件部分的满足程度来激活THEN结论部分。各子结论对应输出变量，以通过聚集确定条件的满足程度来确定结论或子结论的隶属度。通常激活用MIN算子。当规则有加权因子时，应考虑每条规则的加权因子，需采用PROD算子。

3）综合：将各规则的结论汇总获得总的结果。

（7）示例

【例5-4】模糊功能块示例。

END_RULEBLOCK；

END_FUNCTION_BLOCK

3.一致性等级

模糊控制功能块的一致性等级分为三级。

1）基本级（Basic Level）：包括IEC 61131-3定义的功能块和数据类型。

2）扩展级（Extension Level）：包括表5-52允许的可选性能。

3）开放级（Open Level）：IEC 61131本部分未定义的附加性能，由制造商列出。

基本级和扩展级语言元素的基本性能见表5-52。

表5-52 基本级和扩展级语言元素的基本性能

开放级语言元素由制造商规定，例如，可自由定义输入-输出变量的隶属函数，像用高斯函数、指数函数等；隶属函数的点数可多于4点；隶属度取值可从0到1；隶属度的值可以是变量等。