概率分析是研究不确定因素和风险因素按一定概率变动时,对项目方案经济评价指标影响的一种定量分析方法。其目的是为在不确定情况下决策投资项目或方案提供科学依据。
(一)投资方案经济效果的概率描述与决策
1.经济效果的期望值
投资方案经济效果的期望值是指在一定概率分布条件下,投资效果所能达到的概率平均值。其一般表达式为
![]()
式中 E(x)——变量的期望值;
xi——变量xi状态下的取值(i=1,2,…,n);
pi——变量xi出现的概率;
n——未来状态的个数。
2.经济效果的标准差
标准差反映了一个随机变量实际值与其期望值偏离的程度。这种偏离程度在一定意义上反映了投资方案风险的大小。标准差的一般计算公式为
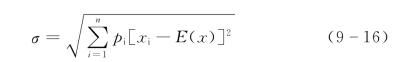
式中 σ——变量x的标准差;
其他符号的意义同式(9-15)。
3.经济效果的变异系数
标准差虽然可以反映随机变量的离散程度,但它是一个绝对量,其大小与变量的数值及期望值大小有关。一般而言,变量的期望值越大,其标准差也越大。特别是需要对不同方案的风险程度进行比较时,标准差往往不能够准确反映风险程度的差异。为此引入另一个指标,称为变异系数。它是标准差与期望值之比,即
![]()
由于变异系数是一个相对数,不会受变量和期望值的绝对值大小的影响,能更好地反映投资方案的风险程度。
当对多个投资方案进行比较时,如果是效益指标,则认为期望值较大的方案较优;如果是费用指标,则认为期望值较小的方案较优。如果期望值相同,则标准差较小的方案风险更低;如果多个方案的期望值与标准差均不相同,则变异系数较小的方案风险更低。
(二)投资方案风险分析
投资方案风险通常可以用达到检验标准的可能性大小来分析判断。这种分析判断的方法有许多种,主要有图表法和解析法。
1.图表法
如果方案经济效果指标的概率分布不明或者无法用分布描述时,或者经济效果指标服从曲线概率分布的情况,则可运用图表法进行风险判断。它一般通过计算各种状态下经济效果指标和对应发生的概率,再通过图表描述出来。
2.解析法
如果状态的分布满足于连续型随机变量的特征,能用分布函数进行刻画,可以直接用解析法判断风险的大小。一般来讲,经济评价指标随机变量倾向于服从正态分布,而这种分布函数能够准确描述不同的净现值所对应发生的概率。通过数值计算,可以较合理的测算出方案最可能达到的净现值。
若项目的净现值服从正态分布N(μ,σ2)即有分布函数
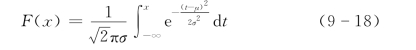
令![]() ,式(9-18)可转化为标准正态分布函数(https://www.xing528.com)
,式(9-18)可转化为标准正态分布函数(https://www.xing528.com)
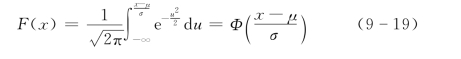
令![]() ,由标准正态分布表可以直接查出x<x0的概率值
,由标准正态分布表可以直接查出x<x0的概率值
![]()
(三)概率分析基础上的风险决策
概率分析可以给出方案经济效果指标的期望值,标准差和变异系数以及经济效果指标的实际值发生在某一区间的概率,这为人们在风险条件下决定方案取舍提供了依据和原则,下面依据这些原则,对风险决策问题的决策方法简单介绍。
1.风险决策的条件
风险决策的条件有:
(1)存在着决策人希望达到的目标(如利润最大或损失最小)。
(2)存在着两个或两个以上可供决策者选择的行动方案。
(3)存在着两个或两个以上不以决策者的主观意志为转移的自然状态。
(4)可以计算出不同方案在不同自然状态下的损益值(即经济效果指标)。
(5)各种自然状态出现的概率可以预测或估计。
2.风险决策的矩阵法
假设对于风险决策问题,有m个方案A1,A2,…,Am;有n个自然状态θ1,θ2,…,θn;每个自然状态θj(j=1,2,…,n)出现的概率为Pj;各方案Ai(i=1,2,…,m)在状态θj(j=1,2,…,m)下的损益值矩阵为Vm×n,即

若以P=(P1,P2,…,Pn)T表示概率向量;E=(E1,E2,…,Em)T表示期望损益值向量,(各元素Ek,k=1,2,…,m为方案AK的期望损益值)。
则有
![]()
表9-1列出了风险决策的矩阵模型。
表9-1 风险决策的矩阵模型

根据期望值原则进行决策:当损益值为费用时,min{Ei|i=1,2,…,m}对应的方案为最优方案;当损益值为收益时,则max{Ei|i=1,2,…,m}对应的方案为最优方案。
3.决策树法
风险决策问题可以利用一种树型决策网络描述与求解,这种方法称为决策树法。图9-1为用决策树描述的风险决策问题实例。
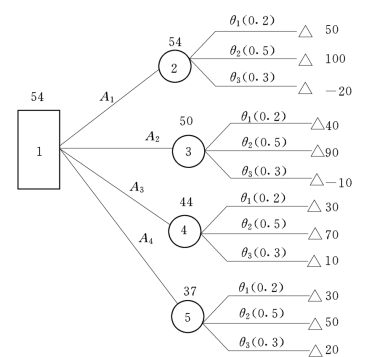
图9-1 用决策树描述的风险决策问题
决策树由不同的节点在分支组成。符号“⌷”表示的节点称为决策节点,由决策节点引出的每一分支表示一个可供选择的方案;符号“○”表示的节点称为状态节点,从状态节点引出的每一分支表示一种可能发生的状态,每一状态分支的末端为结果节点用符号“△”表示。画决策树的顺序是从左至右,决策树画完后,应对每一节点进行编号,以便分析。根据各种状态发生的概率与相应的损益值分别计算每一方案的损益期望值,计算的顺序是从右至左,并将其计算的结果标在相应的节点上,就可以直观地判断出应选择哪个方案,将余下的方案剪掉。
决策树法常用于多级风险决策问题。所谓多级风险决策即需要进行两次或两次以上的决策,才能选出最优方案的决策问题。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




