1.直方图的用途
直方图法即频数分布直方图法，是将收集到的质量数据进行分组整理，绘制成频数分布直方图，用以描述质量分布状态的一种分析方法，所以又称质量分布图法。
通过对直方图的观察与分析，可了解产品质量的波动情况，掌握质量特性的分布规律，对质量状况进行分析判断。
2.直方图的绘制方法
（1）收集整理数据。用随机抽样的方法抽取数据，一般要求数据在50个以上。
【例12-1】 某建筑施工工地浇筑C30混凝土，为对其抗压强度进行质量分析，共收集了50份抗压强度试验报告单，经整理如表12-1所示。
表12-1 数据整理表单位：N/mm2
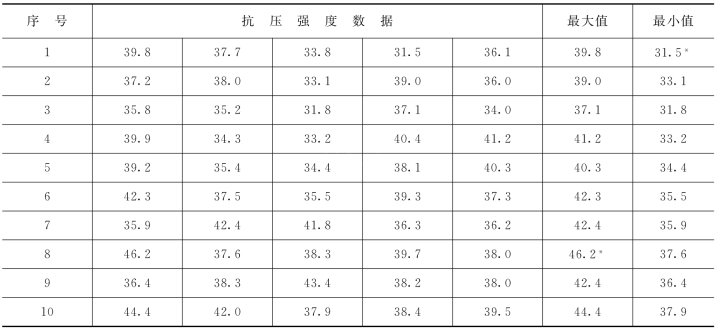
* 最大值中的最大值和最小值中的最小值。
（2）计算极差R。极差R是数据中最大值和最小值之差，本例中：Xmax＝46.2N/mm2，Xmin＝31.5N/mm2，R＝Xmax-Xmin＝14.7N/mm2。
（3）对数据分组。
1）确定组数k。确定组数的原则是分组的结果能正确地反映数据的分布规律。组数应根据数据多少来确定。组数过少，会掩盖数据的分布规律；组数过多，会使数据过于零乱分散，也不能显示出质量分布状况，一般可参考表12-2的经验数值来确定。本例中k＝8。
表12-2 数据分组参考值
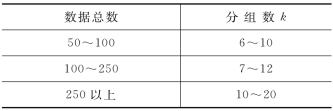
2）确定组距h。组距是组与组之间的间隔，即一个组的范围。各组距应相等，有
极差≈组距×组数
即
因而组数、组距的确定应结合极差综合考虑，适当调整，还要注意数值尽量取整，使分组结果能包括全部变量值，同时也便于以后的计算分析。本例中
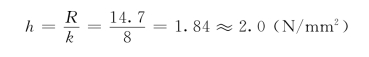
3）确定组限。每组的最大值为上限，最小值为下限，上、下限统称组限。确定组限时应注意各组之间连续，即较低组上限应为相邻较高组下限，这样才不致使数据被遗漏。对恰恰处于组限值上的数据，其解决的办法：一是规定每组上（或下）组限不计在该组内，而应计入相邻较高（或较低）组内；二是将组限值较原始数据精度提高半个最小测量单位。
本例采取第一种办法划分组限，即每组上限不计入该组内。
第一组下限
第一组上限
30.5＋h＝30.5＋2＝32.5（N/mm2）
第二组下限＝第一组上限＝32.5（N/mm2）
第二组上限
32.5＋h＝32.5＋2＝34.5（N/mm2）(www.xing528.com)
以下以此类推，最高组限为
44.5～46.5N/mm2
分组结果覆盖了全部数。
（4）编制数据频数统计表。统计各组频数，可采用唱票形式进行，频数总和应等于全部数据个数。本例频数统计结果见表12-3。
表12-3 频数统计表
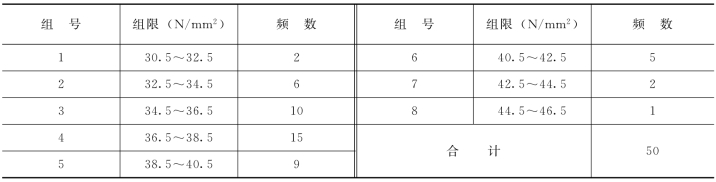
从表12-3中可以看出，浇筑C30混凝土，50个试块的抗压强度是各不相同的，这说明质量特性值是有波动的。但这些数据分布是有一定规律的，就是数据在一个有限范围内变化，且这种变化有一个集中趋势，即强度值在36.5～38.5范围内的试块最多，可把这个范围即第四组视为该样本质量数据的分布中心，随着强度的逐渐增大和逐渐减小，而数据逐渐减少。为了更直观、更形象地表现质量特征值的这种分布规律，应进一步绘制出直方图。
（5）绘制频数分布直方图。在频数分布直方图中，横坐标表示质量特性值，本例中为混凝土强度，并标出各组的组限值。根据表12-3画出以组距为底，以频数为高的k个直方形，便得到混凝土强度的频数分布直方图，见图12-1。
图12-1 混凝土强度分布直方图
3.直方图的观察与分析
（1）观察直方图的形状、判断质量分布状态。作完直方图后，首先要认真观察直方图的整体形状，看其是否属正常型直方图。正常型直方图就是中间高，两侧底，左右接近对称的图形，如图12-2（a）所示。出现非正常型直方图时，表明生产过程或收集数据有问题。这就要求进一步分析判断，找出原因，并采取措施加以纠正。非正常型直方图，归纳起来一般有5种类型，见图12-2。
1）折齿型，是由于分组不当或者组距确定不当出现的，见图12-2（b）。
2）左（或右）缓坡型，主要是由于操作中对上限（或下限）控制太严造成的，见图12-2（c）。
3）孤岛型，是原材料发生变化，或者临时他人顶班作业造成的，见图12-2（d）。
4）双峰型，是由于用两种不同方法或两台设备或两组工人进行生产，然后把两方面数据混在一起整理产生的，见图12-2（e）。
5）峭壁型，是由于数据收集不正常，可能有意识地去掉下限附近的数据，或是在检测过程中存在某种人为因素所造成的，见图12-2（f）。
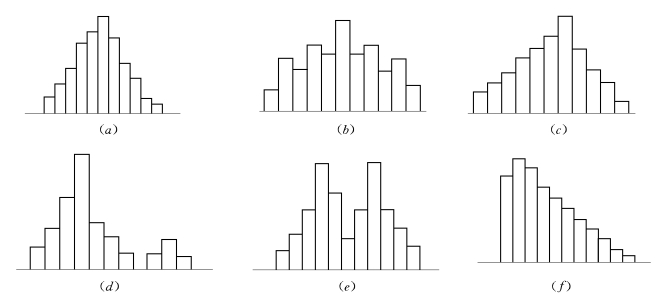
图12-2 常见的直方图
（a）正常型；（b）折齿型；（c）左（或右）缓坡型；（d）孤岛型；（e）双峰型；（f）峭壁型
（2）将直方图与质量标准比较，判断实际生产过程能力。作出直方图后，除观察直方图形状，分析质量分布状态外，再将正常型直方图与质量标准比较，从而判断实际生产过程能力。正常型直方图与质量标准相比较，一般有如图12-3所示6种情况。图12-3中，T表示质量标准要求界限，B表示实际质量特性分布范围。
1）图12-3（a），B在T中间，质量分布中心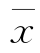
与质量标准中心M重合，实际数据分布与质量标准相比较两边还有一定余地。这样的生产过程是很理想的，说明生产过程处于正常的稳定状态。在这种情况下生产出来的产品可认为全都是合格品。
2）图12-3（b），B虽然落在T内、但质量分布中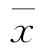
与T的中心M不重合，偏向一边。这样生产状态一旦发生变化，就可能超出质量标准下限而出现不合格品。出现这样情况时应迅速采取措施，使直方图移到中间来。
3）图12-3（c），B在T中间，且B的范围接近T的范围，没有余地，生产过程一旦发生微小的变化，产品的质量特性值就可能超标。这表明产品质量的散差太大，必须采取措施缩小质量分布范围。
4）图12-3（d），B在T中间，但两边余地太大，说明加工过于精细，不经济。在这种情况下，可以对原材料、设备、工艺、操作等控制要求适当放宽些，有目的的使B扩大，从而有利于降低成本。
5）图12-3（e），质量分布范围B已超出标准下限之外，说明已出现不合格品。此时必须采取措施进行调整，使质量分布位于标准之内。
6）图12-3（f），质量分布范围完全超出了质量标准上、下界限，散差太大，产生许多废品，说明过程能力不足，应提高过程能力，使质量分布范围B缩小。
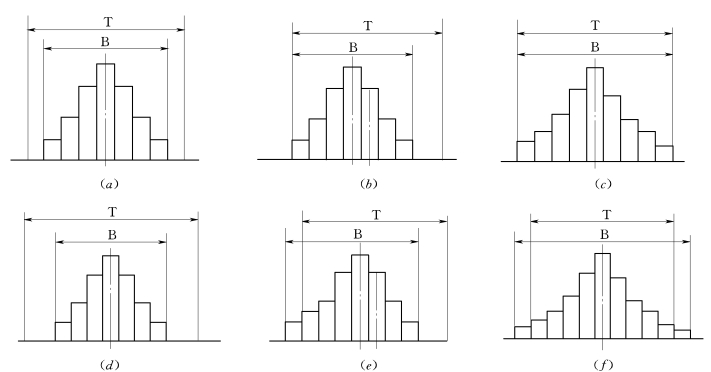
图12-3 实际质量分析与标准比较
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
