费用优化方案在工程施工中的应用

费用优化又称为工期成本优化，即通过分析工期与工程成本（费用）的相互关系，寻求最低工程总成本（总费用）。

1.工期和费用的关系

工程费用包括直接费用和间接费用两部分，直接费用是直接投入到工程中的成本，即在施工过程中耗费的人工费、材料费、机械设备费等构成工程实体相关的各项费用；而间接费用是间接投入到工程中的成本，主要由公司管理费、财务费用和工期变化带来的其他损益（如效益增量和资金的时间价值）等构成。一般情况下，直接费用随工期的缩短而增加，与工期成正比；间接费用随工期的缩短而减少，与工期成反比。如图3-47的总费用曲线中，总存在一个最低的点，即最小的工程总成本C0，与此相对应的工期为最优工期T0，这就是费用优化所寻求的目标。

在图3-47中，直接费用曲线表明当缩短工期时，会造成直接费用的增加。这是因为在施工时为了加快作业速度，必须采取加班加点和多班制等突击作业方式，增加材料、劳动力及机械设备等资源的投入，使得直接投入工程的成本增加。然而，在施工中存在着一个最短工期TS，无论再增加多少直接费用，工期也不能再缩短了。另外，也同样存在着一个正常工期TF，不管怎样再延长工期也不能使直接费用再减少。

为简化计算，如图3-47所示，通常把直接费用曲线1、间接费用曲线2表达为直接费用直线1′、间接费用直线2′。这样可以通过直线斜率表达直接（间接）费用率，即直接（间接）费用在单位时间内的增加（减少）值。如工作i-j的直接费用率ΔCi-j为：

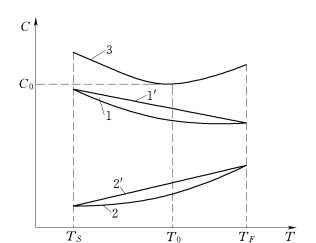
图3-47　工期—费用曲线

1、1′—直接费用曲线、直线；2、2′—间接费用曲线、直线；3—总费用曲线
TS—最短工期；T0—最优工期；TF—正常工期；C0—最低总成本

式中 CCi-j——将工作持续时间缩短为最短持续时间后完成该工作所需的直接费用；

CNi-j——在正常条件下完成工作i-j所需的直接费用；

DNi-j——工作i-j的正常持续时间；

DCi-j——工作i-j的最短持续时间。

2.工作和费用的关系

根据各项工作的性质不同，其工作持续时间和费用之间的关系通常有以下两种情况。

（1）连续型变化关系。当工作的费用随着工作持续时间的改变而改变，其介于正常持续时间和最短持续时间之间的任意持续时间的费用可根据其费用斜率计算出来，称为连续型变化关系。

如某工序为连续型变化关系，其正常持续时间DN为16天，所需直接费用C16为500元；最短持续时间DC为10天，所需直接费用C10为1100元，则当工作为12天，所需直接费用C12为

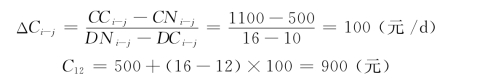
（2）非连续型变化关系。当工作的直接费用与持续时间之间的关系是根据不同施工方案分别估算的，其介于正常持续时间与最短持续时间之间的关系不是线性关系，不能通过费用斜率计算，只能存在几种情况供选择，称为非连续型变化关系。

如某工序为非连续型变化关系，其持续时间、所需直接费用有三种施工方法可供选择，如表3-8所示。

表3-8　某工序持续时间与费用表

在工程施工中，根据工期、成本要求，制定施工方案，确定持续时间、直接费用。

3.费用优化的步骤

寻求最低费用和最优工期的基本思路是从网络计划的各活动持续时间和费用的关系中，依次找出能使计划工期缩短，而又能使直接费用增加最少的活动，不断地缩短其持续时间，同时考虑其间接费用叠加，即可求出工程费用最低时的最优工期和工期确定时相应的最低费用。

（1）绘出网络图，按工作的正常持续时间确定计算工期和关键线路。

（2）计算间接费用率ΔC′和各项工作的直接费用率ΔCi-j。

（3）当只有一条关键线路时，应找出直接费用率ΔCi-j最小的一项关键工作，作为缩短持续时间的对象；当有多条关键线路时，应找出组合直接费用率∑{ΔCi-j}最小的一组关键工作，作为缩短持续时间的对象。

（4）对选定的压缩对象缩短其持续时间，缩短值ΔT必须符合两个原则：一是不能压缩成非关键工作；二是缩短后其持续时间不小于最短持续时间。（5）计算压缩对象缩短后总费用的变化Ci

（6）当Ci≤0，重复上述（3）～（5）步骤，一直计算到Ci＞0，即总费用不能降低为止，费用优化即告完成。

4.费用优化的示例

【例3-10】已知网络计划如图3-48所示，箭线下方括号外为工作正常持续时间DN，括号内为工作最短持续时间DC，各工作所需直接费用见表3-9，假定间接费用率为180元/d，试对该网络计划进行费用优化。

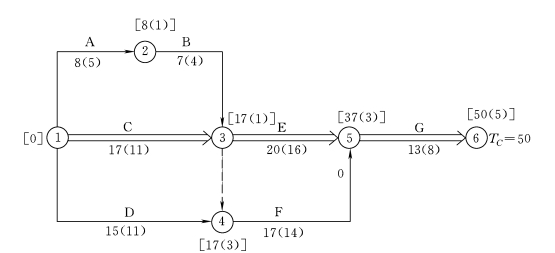
图3-48　某工程网络计划

表3-9　各工序直接费用表单位：元

解（1）按工作的正常持续时间确定计算工期和关键线路。

如图3-48所示，用标号法求得关键线路为：①—③—⑤—⑥，关键工作为：C、E、G。计算工期TC＝50d，工程总费用为

C＝10300＋50×180＝19300（元）

（2）计算各项工作的直接费用率ΔCi-j(www.xing528.com)

A工作

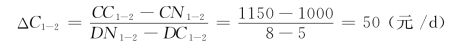
B工作

同理，可得出各工作的直接费用率，如图3-49所示。

图3-49　各项工作的直接费用率

（3）从图3-49可知，应确定直接费用率最小的关键工作C工作为压缩对象，在不改变关键线路情况下，只能缩短2天，如图3-50所示。则

计算工期

TC1＝50-2＝48（d）

总费用变化

C1＝2×50-2×180＝-260元＜0

（4）从图3-50可知，关键线路已变为2条：①—③—⑤—⑥和①—②—③—⑤—⑥，关键工作为A、B、C、E、G。因为C工作费用率最小，应选择C工作来组合压缩方案，此时C工作组合压缩方案有两个。

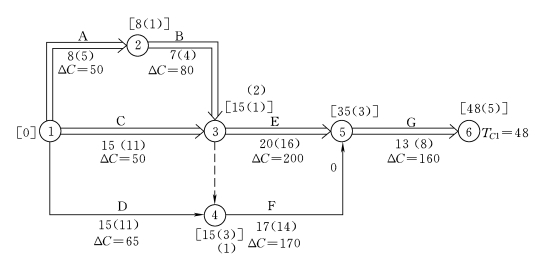
图3-50　第一次压缩

压缩A、C工作

∑{ΔC}＝50＋50＝100（元/d）

压缩B、C工作

∑{ΔC}＝50＋80＝130（元/d）

应确定组合直接费用率最小的关键工作A、C工作为压缩对象，在不改变关键线路情况下，A、C工作同时缩短3天，如图3-51所示。则

计算工期

TC2＝48-3＝45（d）

总费用变化

C2＝3×（50＋50）-3×180＝-240元＜0

（5）从图3-51可知，关键线路已变为3条：①—③—⑤—⑥、①—②—③—⑤—⑥和①—④—⑤—⑥，关键工作为A、B、C、D、E、F、G。此时C工作组合压缩方案有两个。

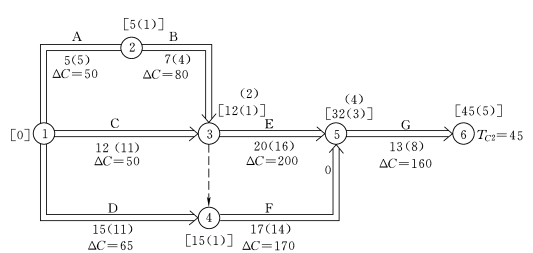
图3-51　第二次压缩

压缩B、C、D工作

压缩B、C、F工作

因这两个方案都大于G工作的直接费用率，故确定G工作为压缩对象，因G工作为3条关键线路共有，可缩短5天至最短持续时间，如图3-52所示。则

计算工期

总费用变化

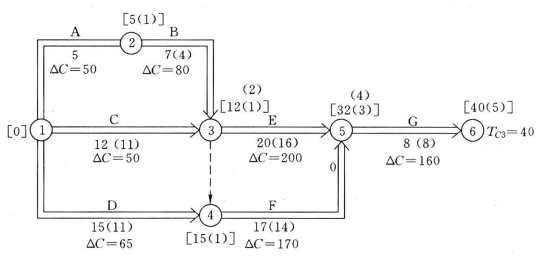
图3-52　优化完成

因再压缩工期，Ci＞0，工程总费用将会增加，即费用优化完成。最低总费用为

最优工期为40天。