单代号搭接网络的计算方法

单代号搭接网络计划的计算与前述一般单代号网络计划的计算原理基本相同，现介绍图上计算法如下。

1.单代号搭接网络图时间参数的计算

（1）计算工作的最早开始时间和最早完成时间。工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始，顺着箭线方向依次进行。

一般搭接网络的起点为虚节点，故与网络计划起点节点相联系的工作，其最早开始时间为零，即

与网络计划起点节点相联系的工作，其最早完成时间应等于其最早开始时间与持续时间之和，即

其他工作的最早开始时间和最早完成时间应根据时距按下列公式计算：

相邻时距为STS时

相邻时距为FTF时

相邻时距为STF时

相邻时距为FTS时

当有多项紧前工作时或有混合连接关系时，分别按式（3-46）～（3-49）计算，取最大值为工作的最早开始时间。

当出现最早开始时间为负值时，应将该工作与起点节点用虚箭线相连接，并确定其时距为

工作最早完成时间按下式计算

当出现有最早完成时间的最大值的中间工作时，应将该工作与终点节点用虚箭线相连接，并确定其时距为

（2）网络计划的计算工期TC。一般搭接网络的终点为虚节点，TC等于网络计划的终点节点n的最早完成时间EFn，即

（3）相邻两项工作之间的时间间隔LAGi，j。相邻两项工作在满足时距外，如还有多余的时间间隔，则按下列公式计算：

相邻时距为STS时，如ESj＞ESi＋STSi，j，则时间间隔为

相邻时距为FTF时，EFj＞EFi＋FTFi，j，则时间间隔为

相邻时距为STF时，EFj＞ESi＋STFi，j，则时间间隔为

相邻时距为FTS时，ESj＞EFi＋FTSi，j，则时间间隔为

当相邻两项工作存在混合连接关系时，分别按式（3-54）～（3-57）计算，取最小值为工作的时间间隔。

当相邻两项工作无时距时，为一般单代号网络，按式（3-35）计算

LAGi，j＝ESj-EFi

（4）工作总时差TFi。工作i的总时差TFi应从网络计划的终点节点开始，逆着箭线方向依次逐项计算。

网络计划终点节点n的总时差TFn，如计划工期等于计算工期，其值为零，按式（3-36）计算

TFn＝TP-EFn＝0

其他工作i的总时差TFi等于该工作的各个紧后工作j的总时差TFj加该工作与其紧后工作之间的时间间隔LAGi，j之和的最小值，按式（3-37）计算

TFi＝min[TFj＋LAGi，j]

（5）工作自由时差FFi。网络计划终点节点n的自由时差FFi等于计划工期TP减去该工作的最早完成时间EFn，按式（3-38）计算

FFn＝TP-EFn

其他工作i的自由时差FFi等于该工作与其紧后工作j之间的时间间隔LAGi，j最小值，按式（3-39）计算

FFi＝min[LAGi，j]

（6）工作的最迟开始时间和最迟完成时间。网络计划终点节点n的最迟完成时间LFn应按网络计划的计划工期确定，按式（3-40）计算

LFn＝TP

其他工作i的最迟完成时间LFi等于该工作的最早完成时间EFi加上其总时差TFi之和，按式（3-41）计算

LFi＝EFi＋TFi

工作i的最迟开始时间LSi等于该工作的最早开始时间ESi加上其总时差TFi之和，按式（3-42）、（3-43）计算

LSi＝ESi＋TFi

或

LSi＝LFi-Di(www.xing528.com)

2.关键工作和关键线路的确定

（1）关键工作：总时差最小的工作是关键工作。

（2）关键线路的确定按以下规定：从起点节点开始到终点节点均为关键工作，且所有工作的时间间隔为零的线路为关键线路。

3.单代号搭接网络计划时间参数计算示例

【例3-6】已知网络计划如图3-33所示，若计划工期等于计算工期，试计算各项工作的六个时间参数并确定关键线路，标注在网络计划上。

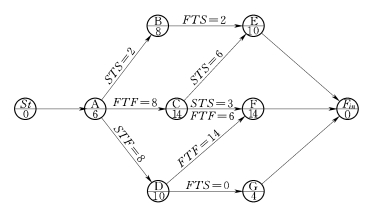
图3-33　某工程单代号搭接网络计划

解（1）计算各项工作的最早开始时间和最早完成时间

由于D工作的ESD＝-2，应加虚箭线与起点节点相连，STS＝0：

ESD＝ESst＋STSst，D＝0＋0＝0--EFD＝ESD＋DD＝0＋10＝10

由于E工作有两个紧前工作，应分别计算取大值

ESE＝EFB＋FTSB，E＝10＋2＝12--ESE＝ESC＋STSC，E＝0＋6＝6

应取ESE＝12，则

EFE＝ESE＋DE＝12＋10＝22

由于F工作有两个紧前工作、混合连接关系，应分别计算取大值

ESF＝ESC＋STSC，F＝0＋3＝3

ESF＝EFC＋FTFC，F-DF＝14＋6-14＝6

ESF＝EFD＋FTFD，F-DF＝10＋14-14＝10

应取ESF＝10，则

EFF＝ESF＋DF＝10＋14＝24

ESG＝EFD＋FTSD，G＝10＋0＝10--EFG＝ESG＋DG＝10＋4＝14

ESFin＝max[EFE，EFF，EFG]＝max[22，24，14]＝24

EFFin＝ESFin＝24

已知计划工期等于计算工期，故有

TP＝TC＝EFFin＝24

（2）计算相邻两项工作之间的时间间隔LAGi，j

LAGst，A＝ESA-EFst＝0-0＝0

LAGst，D＝ESD-ESst-STSst，D＝0-0-0＝0

LAGA，B＝ESB-ESA-STSA，B＝2-0-2＝0

LAGA，C＝EFC-EFA-FTFA，C＝14-6-8＝0

LAGA，D＝EFD-ESA-STFA，D＝10-0-8＝2

LAGB，E＝ESE-EFB-FTSB，E＝12-10-2＝0

LAGC，F＝min[（ESF-ESC-STSC，F），（EFF-EFC-FTFC，F）]

＝min[（10―0―3），（24―14―6）]＝4

其他工作的时间间隔的计算以次类推，如图3-34所示。

图3-34　某工程单代号搭接网络计划计算

（3）计算工作的总时差TFi。已知计划工期等于计算工期：TP＝TC＝24，故终点节点的总时差为零，即

其他工作总时差为：

TFFin＝0

TFE＝TFFin＋LAGE，Fin＝0＋2＝2

TFF＝TFFin＋LAGF，Fin＝0＋0＝0

TFG＝TFFin＋LAGG，Fin＝0＋10＝10

TFB＝TFE＋LAGB，E＝2＋0＝2

TFC＝min[（TFE＋LAGC，E），（TFF＋LAGC，F）]＝min[（2＋6），（0＋4）]＝4

TFD＝min[（TFG＋LAGD，G），（TFF＋LAGD，F）]＝min[（6＋0），（0＋0）]＝0

TFA＝min[（TFB＋LAGA，B），（TFC＋LAGA，C），（TFD＋LAGA，D）]

＝min[（2＋0），（4＋0），（0＋2）]＝2

TFst＝min[（TFA＋LAGst，A），（TFD＋LAGst，D）]＝min[（2＋0），（0＋0）]＝0

（4）计算工作的自由时差FFi。已知计划工期等于计算工期：TP＝TC＝24，故终点节点的自由时差为

（5）计算工作的最迟开始时间LSi和最迟完成时间LFi。按式（3-41）、（3-42）计算LFi、LSi，计算结果见图3-34。

（6）关键工作和关键线路的确定。根据计算结果，总时差为零的工作：D、F为关键工作；从起点节点开始到终点节点均为关键工作，且所有工作之间时间间隔为零的线路：St—D—F—Fin为关键线路，用双箭线标示在图3-34中。