双代号网络图时间参数计算方法

双代号网络计划时间参数计算的目的主要有三个：一是计算工期，做到工程进度安排心中有数；二是确定网络计划的关键工作、关键线路，以便在工程施工中抓住主要矛盾；三是为网络计划的执行、优化和调整提供明确的时间参数。

双代号网络计划时间参数的计算方法很多，一般常用的有：按工作计算法和按节点计算法进行计算；在计算方式上又有分析计算法、表上计算法、图上计算法、矩阵计算法和电算法等。本节只介绍按工作、节点计算法在图上进行计算的方法，由于各种方法在本质上都是一样的，学会工作图上计算法、节点图上计算法，其他方法可以举一反三。

1.时间参数的概念及其符号

（1）工作持续时间（Di-j）。工作持续时间是对一项工作规定的从开始到完成的时间。在双代号网络计划中，工作i-j的持续时间用Di-j表示。

（2）工期（T）。工期泛指完成任务所需要的时间，一般有以下三种：

1）计算工期：根据网络计划时间参数计算出来的工期，用TC表示。

2）要求工期：任务委托人所提出的指令性工期，用TR表示。

3）计划工期：根据要求工期和计算工期所确定的作为实施目标的工期，用TP表示。

当已规定了要求工期时，网络计划的计划工期不应大于要求工期；当未规定要求工期时，可令计划工期等于计算工期。

（3）工作的6个时间参数分别是：

1）工作最早开始时间（ESi-j）：是指在各紧前工作全部完成后，本工作有可能开始的最早时刻。工作i-j的最早开始时间用ESi-j表示。

2）工作最早完成时间（EFi-j）：是指在各紧前工作全部完成后，本工作有可能完成的最早时刻。工作i-j的最早完成时间用EFi-j表示。

3）工作最迟开始时间（LSi-j）：是指在不影响整个任务按期完成的前提下，本工作必须开始的最迟时刻。工作i-j的最迟开始时间用LSi-j表示。

4）工作最迟完成时间（LFi-j）：是指在不影响整个任务按期完成的前提下，本工作必须完成的最迟时刻。工作i-j的最迟完成时间用LFi-j表示。

5）总时差（TFi-j）：是指在不影响总工期的前提下，本工作可以利用的机动时间。工作i-j的总时差用TFi-j表示。

6）自由时差（FFi-j）：是指在不影响其紧后工作最早开始的前提下，本工作可以利用的机动时间。工作i-j的自由时差用FFi-j表示。

（4）节点的两个时间参数包括：

1）节点最早时间（ETi）：是指该节点的内向箭线全部完成，外向箭线有可能开始的最早时刻。节点i的最早时间用ETi表示。

2）节点最迟时间（LTi）：是指在不影响终点节点最迟时间的前提下，该节点的内向箭线最迟必须完成的时间。节点i的最迟时间用LTi表示。

2.工作图上计算法

按工作图上计算法计算网络计划中各时间参数，其计算结果应直接标注在箭线的上方，如图3-16所示。

工作图上计算法的计算步骤为：

（1）工作最早开始时间和最早完成时间的计算。从定义可知，工作最早时间参数受到紧前工作的约束，故其计算顺序应从左向右，从起点节点开始，顺着箭线方向依次逐项计算，一直到终点节点。

当网络计划没有规定开始时间，从起点节点出发的工作的最早开始时间为零。如网络计划起点节点的编号为1，则：

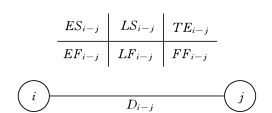
图3-16　按工作计算时间参数标注形式

每个工作最早完成时间等于工作的最早开始时间加上其持续时间：

除以起点节点起始工作外，每个工作的最早开始时间等于各紧前工作的最早完成时间EFh-i的最大值

即

（2）确定计算工期TC。计算工期等于以网络计划的终点节点为箭头节点的各个工作的最早完成时间的最大值。当网络计划终点节点的编号为n时，计算工期为

当无要求工期的限制时，取计划工期等于计算工期，即

TP＝TC

（3）工作最迟开始时间和最迟完成时间的计算。从定义可知，工作最迟时间参数受到紧后工作的约束，故其计算顺序应从右向左，从终点节点起，逆着箭线方向依次逐项计算，一直到起点节点。

以网络计划的终点节点（j＝n）结束的工作的最迟完成时间等于计划工期TP，即

每个工作的最迟开始时间等于工作最迟完成时间减去其持续时间

除以终点节点结束的工作外，每个工作的最迟完成时间等于各紧后工作的最迟开始时间LSj-k的最小值

即

（4）计算工作总时差。总时差是指在不影响总工期的前提下，本工作可以利用的机动时间。总时差等于其最迟开始时间减去最早开始时间，或等于最迟完成时间减去最早完成时间

或

（5）计算工作自由时差。自由时差是指在不影响其紧后工作最早开始时间的前提下，本工作可以利用的机动时间。当工作i-j有紧后工作j-k时，其自由时差应为

或

以网络计划的终点节点（j＝n）结束的工作，其自由时差FFi-n应按网络计划的计划工期TP确定，即

（6）关键工作和关键线路的确定。当TP＝TC时，总时差为正值、零，总时差等于零的工作为关键工作；当TP＞TC或TP＜TC时，总时差为正值、负值，总时差最小的工作为关键工作。

自始至终全部由关键工作组成的线路为关键线路，即线路上总的工作持续时间最长的线路为关键线路。网络图上的关键线路可用双线、粗线或彩色线标注。

3.工作图上计算法示例

【例3-1】已知网络计划如图3-17所示，若计划工期等于计算工期，试计算各项工作的6个时间参数并确定关键线路，标注在网络计划上。

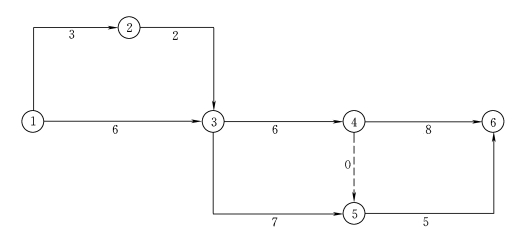
图3-17　某双代号网络计划

解（1）计算各项工作的最早开始时间和最早完成时间。从起点节点（节点）开始顺着箭线方向依次逐项计算到终点节点（节点）。

以网络计划起点节点开始的各工作的最早开始时间为零

ES1—2＝ES1—3＝0

计算各项工作的最早开始和最早完成时间

将以上计算结果标注在图3-18中的相应位置。

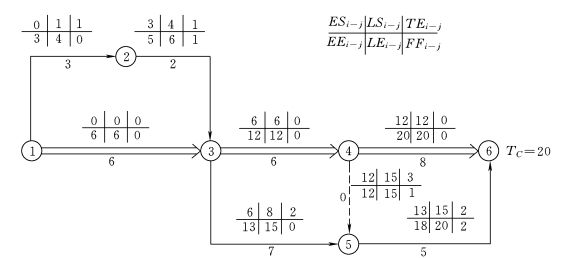
图3-18　某双代号网络计划工作图上计算法

（2）确定计算工期TC及计划工期TP。计算工期

TC＝max[EF5—6，EF4—6]＝max[18，20]＝20

已知计划工期等于计算工期，即

TP＝TC＝20

（3）计算各项工作的最迟开始时间和最迟完成时间。从终点节点（节点）开始逆着箭线方向依次逐项计算到起点节点（节点）。以网络计划终点节点结束的工作的最迟完成时间等于计划工期

LF4—6＝LF5—6＝20

计算各项工作的最迟开始和最迟完成时间

LS4—6＝LF4—6-D4—6＝20-8＝12

LS5—6＝LF5—6-D5—6＝20-5＝15

LF3—5＝LF4—5＝LS5—6＝15

LS3—5＝LF3—5-D3—5＝15-7＝8

LS4—5＝LF4—5-D4—5＝15-0＝15

LF3—4＝min[LS4—5，LS4—6]＝min[15，12]＝12

LS3—4＝LF3—4-D3—4＝12-6＝6

LF1—3＝LF2—3＝min[LS3—4，LS3—5]＝min[6，8]＝6

LS1—3＝LF1—3-D1—3＝6-6＝0

LS2—3＝LF2—3-D2—3＝6-2＝4

LF1—2＝LS2—3＝4

LS1—2＝LF1—2-D1—2＝4-3＝1

将以上计算结果标注在图3-18中的相应位置。

（4）计算各项工作的总时差：TFi-j，可以用工作的最迟开始时间减去最早开始时间或用工作的最迟完成时间减去最早完成时间

TF1—2＝LS1—2-ES1—2＝1-0＝1

或：

TF1—2＝LF1—2-EF1—2＝4-3＝1

TF1—3＝LS1—3-ES1—3＝0-0＝0

TF2—3＝LS2—3-ES2—3＝4-3＝1

TF3—4＝LS3—4-ES3—4＝6-6＝0

TF3—5＝LS3—5-ES3—5＝8-6＝2

TF4—5＝LS4—5-ES4—5＝15-12＝3

TF4—6＝LS4—6-ES4—6＝12-12＝0

TF5—6＝LS5—6-ES5—6＝15-13＝2

将以上计算结果标注在图3-18中的相应位置。(www.xing528.com)

（5）计算各项工作的自由时差：TFi-j，等于紧后工作的最早开始时间减去本工作的最早完成时间

FF1—2＝ES2—3-EF1—2＝3-3＝0

FF1—3＝ES3—4-EF1—3＝6-6＝0

FF2—3＝ES3—5-EF2—3＝6-5＝1

FF3—4＝ES4—6-EF3—4＝12-12＝0

FF3—5＝ES5—6-EF3—5＝13-13＝0

FF4—5＝ES5—6-EF4—5＝13-12＝1

FF4—6＝TP-EF4—6＝20-20＝0

FF5—6＝TP-EF5—6＝20-18＝2

将以上计算结果标注在图3-18中的相应位置。

（6）确定关键工作及关键线路。在图3-18中，最小的总时差是0。所以，凡是总时差为0的工作均为关键工作，即关键工作是：1—3，3—4，4—6。

全由关键工作组成的关键线路是：①—③—④—⑥。关键线路用双箭线进行标注，如图3-18所示。

（7）时差分析。首先分析关键工作，可知其总时差等于0，自由时差也都等于0，即关键工作没有任何机动时间；其次分析非关键工作，可知其总时差大于0，自由时差可大于0（如工作②—③、④—⑤、⑤—⑥），自由时差也可等于0（如工作①—②、③—⑤），即自由时差为总时差的一部分，其值小于或等于总时差。总时差不仅用于本工作，而且与前后工作都有关系，它为一条线路或线段所共有，而自由时差对后续工作没有影响，利用某项工作的自由时差时，其后续工作仍可按最早可能开始的时间开始。当以关键线路上的节点为结束节点的工作，其自由时差与总时差相等（如工作②—③、⑤—⑥）。

4.节点图上计算法

按节点图上计算法计算网络计划中各时间参数，其计算结果应直接标注在节点的上方，如图3-19所示。

节点图上计算法的计算步骤为：

（1）节点最早时间的计算。节点最早时间参数应从左向右，从起点节点开始，顺着箭线方向依次逐项计算，一直到终点节点。

当网络计划没有规定开始时间，起点节点的最早时间为零。如网络计划起点节点的编号为1，则

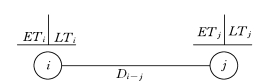
图3-19　按工作计算时间参数标注形式

除起点节点外，每个节点的最早时间等于各内向箭线的箭尾节点最早时间与箭线持续时间之和的最大值

（2）确定计算工期。计算工期等于网络计划的终点节点最早时间。当网络计划终点节点的编号为n时，计算工期为

当无要求工期的限制时，取计划工期等于计算工期，即

TP＝TC

（3）节点最迟时间的计算。节点最迟时间参数应从右向左，从终点节点起，逆着箭线方向依次逐项计算，一直到起点节点。

终点节点n的最迟时间等于计划工期TP，即

除终点节点外，每个节点的最迟时间等于各外向箭线箭头节点的最迟时间与箭线持续时间之差的最小值

（4）计算工作总时差。总时差等于工作箭头节点最迟时间减去箭尾节点最早时间再减去工作持续时间

（5）计算工作自由时差。自由时差等于工作箭头节点最早时间减去箭尾节点最早时间再减去工作持续时间应为

（6）工作的最早、最迟时间参数。工作的最早开始时间、最早完成时间参数是与节点最早时间对应的

工作的最迟开始时间、最迟完成时间参数是与节点最迟时间对应的

（7）关键工作和关键线路的确定。关键工作和关键线路的确定与工作计算法确定原则是一致的。

5.节点图上计算法示例

【例3-2】已知网络计划如图3-17所示，若计划工期等于计算工期，试用节点图上计算法计算各时间参数并确定关键线路，标注在网络计划上。

解（1）节点最早时间的计算

ET1＝0

ET2＝0＋3＝3

ET3＝max[（0＋6），（3＋2）]＝6

ET4＝6＋6＝12

ET5＝max[（12＋0），（6＋7）]＝13

ET6＝max[（12＋8），（13＋5）]＝20

将以上计算结果标注在图3-20中的相应位置。

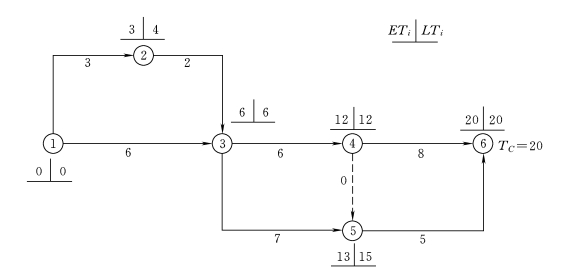
图3-20　某双代号网络计划节点图上计算法

（2）确定计算工期TC，计算工期

TC＝ET6＝20

已知计划工期等于计算工期，即

TP＝TC＝20

（3）节点最迟时间的计算

LT6＝TP＝20

LT5＝20-5＝15

LT4＝min[（20-8），（15-0）]＝12

LT3＝min[（12-6），（15-7）]＝6

LT2＝6-2＝4

LT1＝min[（4-3），（6-6）]＝0

将以上计算结果标注在图3-20中的相应位置。

（4）计算工作时间参数

按式（3-20）～式（3-25）计算工作的总时差，自由时差，工作最早开始、完成时间，工作最迟开始、完成时间。计算结果见图3-18。

6.节点标号法

在前面网络图计算中，是以总时差最小的工作确定为关键工作，而自始至终全部由关键工作组成的线路为关键线路。实际上只要计算节点最早时间参数并标出源节点编号，就可寻找到网络图中持续时间最长的线路，即关键线路和关键工作，这种方法称为节点标号法。

通过节点标号法，不需计算全部时间参数，就可快速确定网络计划的计算工期和关键线路，便于在网络计划编制中，对网络计划做出调整、优化。

（1）节点标号法的计算步骤：

1）计算节点的最早时间：按式（3-15）、（3-16），从左向右计算各节点的最早时间ETi。

2）标出源节点号：除起点节点外，每个节点标出该节点ETi是由哪一个节点计算得来的，即标出源节点号。

3）确定计算工期：计算工期等于网络计划的终点节点最早时间，即式（3-17）。

4）确定关键线路和关键工作：从网络计划终点节点开始，从右向左，逆箭线方向，按源节点号到达起点节点的线路就是网络图中持续时间最长的线路，即关键线路。在关键线路上的工作为关键工作，关键线路可用双线、粗线或彩色线标注。

（2）节点标号法的计算示例。

【例3-3】已知网络计划如图3-21所示，试用节点标号法确定计算工期和关键线路，标注在网络计划上。

图3-21　某双代号网络计划

解（1）节点最早时间的计算

ET1＝0

ET2＝0＋5＝5

源节点号：（1）

ET3＝max[（0＋6），（5＋0）]＝6

源节点号：（1）

源节点号：（2）

ET4＝5＋3＝8

ET5＝6＋4＝10

源节点号：（3）

ET6＝max[（8＋4），（10＋5）]＝15

源节点号：（5）

ET7＝max[（15＋0），（10＋6）]＝16

源节点号：（5）

ET8＝max[（15＋8），（16＋9）]＝25

源节点号：（7）

将以上计算结果标注在图3-22中的相应位置。

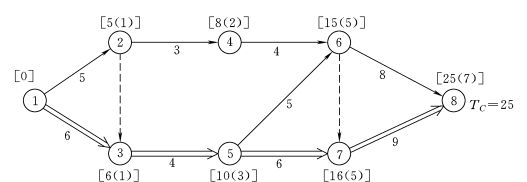
图3-22　某双代号网络计划节点标号法示例

（2）确定计算工期

TC＝ET8＝25

（3）确定关键线路和关键工作。从终点节点⑧开始，逆箭线方向，按源节点号到达起点节点①的线路为⑧—⑦—⑤—③—①，即为关键线路。该线路上的1—3、3—5、5—7、7—8为关键工作。

关键线路用双线表示，见图3-22。