常温下球墨铸铁的静态抗拉性能分析

在力学性能中，常温静态抗拉强度是最基本的性能。在各种工程材料标准中，往往是根据材料的抗拉强度划分牌号。世界各国的球墨铸铁标准也都是按抗拉强度分类的。

（一） 抗拉强度和伸长率

一般来说，材料的伸长率随抗拉强度的增加而降低。图14-1示出了各种基体组织球墨铸铁的抗拉强度和伸长率的关系。其中，P+F表示珠光体和铁素体混合基体组织，ADI表示等温淬火球墨铸铁。对于珠光体—铁素体基体组织的球墨铸铁，伸长率δ （%）和抗拉强度σb（MPa）的关系，可用式（14-1）表示：

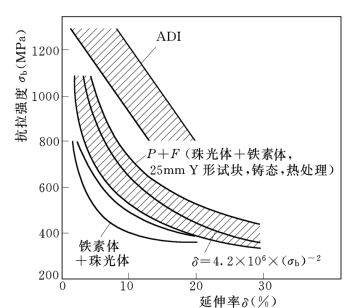
图14-1　各种球墨铸铁的抗拉强度和伸长率的关系

经铁素体化热处理后，伸长率可达30%；高强度的珠光体球墨铸铁具有百分之几的伸长率。

等温淬火球墨铸铁（ADI）的抗拉强度—伸长率的范围与珠光体—铁素体基体组织的球墨铸铁相比，具有高强度和高伸长率的特征，即使抗拉强度为800～1000MPa，其伸长率仍能维持10%以上；当抗拉强度为1000～1300MPa时，仍能得到5%～8%的伸长率。

（二） 屈服强度

屈服强度又称屈服点，也称屈服极限。由于球墨铸铁呈连续屈服行为，通常将0．2%塑性变形应力σ0．2称为0．2%屈服强度，视为与屈服点相当。对于塑性变形小的球墨铸铁（如高强度珠光体球墨铸铁），有时也有用0．1%塑性变形应力σ0．1表征，称为0．1%屈服强度。球墨铸铁的屈服强度一般是抗拉强度的0．6～0．8倍。或者，采用屈服比 （σ0．2/σb 即0．2%屈服强度/抗拉强度）表征球墨铸铁的抗塑性变形能力，它比碳钢的屈服比（一般在0．5～0．6）要高。

等温淬火球墨铸铁（ADI）的屈服比在0．6～0．85之间，这取决于化学成分和采取的热处理制度。随着抗拉强度的增加，其屈服比有稍许增加。此时，等温淬火球墨铸铁的比例极限（弹性极限）大约是σ0．2屈服强度的70%～80%，是抗拉强度的50%～60%。

（三） 弹性模量

球墨铸铁的弹性模量一般在140～180GPa之间；普通灰铸铁的弹性模量在80～130GPa之间；而普通碳钢的弹性模量则在200～210GPa之间。也就是说，球墨铸铁的弹性模量是普通碳钢的70%～80%。球墨铸铁的弹性模量与其抗拉强度有关，抗拉强度越高，则弹性模量也就越高。因此，球墨铸铁的弹性模量主要取决于基体的抗拉强度，但是，它也与石墨球的面积比率有关。

若将球墨铸铁看作是由基体和球状石墨组成的复合材料，其弹性模量可由复合法则表示，弹性模量Ec可由式（14-2）估算：

式中 Em——基体的弹性模量；

Eg——石墨的弹性模量；

fg——石墨的面积比率。

石墨的弹性模量Eg≈5GPa，由于Eg≪Em，故弹性模量Ec≈Em （1-fg）。

当石墨的面积比率为8%～15%，Em=205GPa时，则Ec=174～189GPa（计算值）。

但是，球墨铸铁弹性模量的实测值却小于上述计算值，这可能是呈弹性变形的球状石墨的应力集中效应所致。根据Paul理论，石墨面积比率约为12%的球墨铸铁弹性模量应在136～183GPa之间。

现以石墨面积比率11．8%、石墨平均球径29μm的球墨铸铁为例，计算得出的弹性模量Ec=159～172GPa，实测结果得出的弹性模量Ec=152～181GPa，由此得出的两种结果很接近。

当基体和石墨的泊松比（横向应变/纵向应变）分别为0．29和0．16时，由此计算得出的泊松比ν=0．275～0．30；由实际测量得出的泊松比ν=0．25～0．33。由此表明，实测与计算结果相符。(www.xing528.com)

在弹性变形范围内，由于石墨的弹性模量和强度与基体相比甚小，通常几乎都把石墨球作为空洞处理。不过，石墨球对压缩具有抗力，并且按照载荷方向能显示出与钢相当的弹性模量，故应将石墨球看作是变形抗力的一部分。石墨球可使弹性模量升高的作用，与石墨的结构、致密程度密切相关，其作用程度可达20%。

（四） 硬度

硬度与抗拉强度有良好的相关性。钢铁材料均具有相应的直线关系。对于结构钢，其抗拉强度大约是其布氏硬度的1/3 （σb ≈1/3 HBS）；对于灰铸铁，布氏硬度HBS=100+4．3σb。对于球墨铸铁，也有类似的关系式。

图14-2所示为布氏硬度与抗拉强度的关系。可见，包括铸态、退火态、热处理油冷（淬火态）和热处理空冷 （正火态）的球墨铸铁的布氏硬度和抗拉强度之间一般均呈直线关系。对于铁素体—珠光体混合基体的球墨铸铁，具有关系式（14-3）：

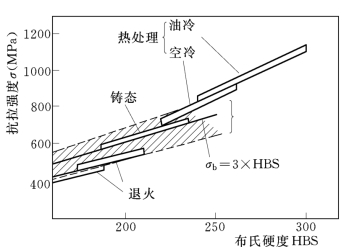
图14-2　布氏硬度与抗拉强度的关系

平均值

式中 σb——抗拉强度（MPa）；

HBS——布氏硬度。

图14-2中，σb＞800MPa的范围对应的是热处理态的球墨铸铁，此时的关系可用式（14-4）表示：

由于球墨铸铁的抗拉强度与其伸长率具有良好的相关性，因此，球墨铸铁的硬度和伸长率之间也具有相关性。据报导的实验结果，铸态、退火态、正火态和淬火态（油冷）球墨铸铁的伸长率和硬度之间均有相应的关系（见图14-3）。

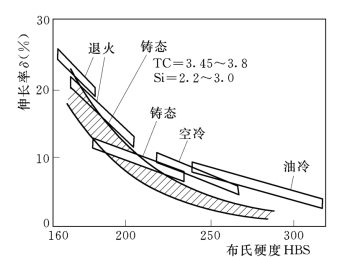
图14-3　布氏硬度和伸长率的关系

图14-4　球墨铸铁的珠光体面积比率与洛氏硬度HRB的关系

也可以通过基体组织中铁素体—珠光体的面积比率来估算硬度值。图14-4是洛氏硬度HRB和珠光体面积比率的关系。可见，两者之间具有良好的线性关系。

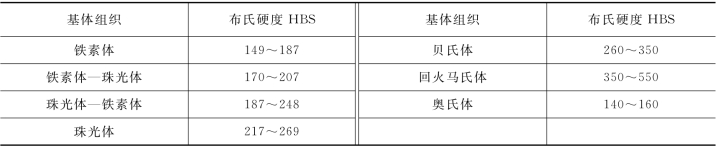
球墨铸铁的基体组织决定了它具有相应的硬度，表14-1示出各种基体组织球墨铸铁的硬度范围。

表14-1　各种基体组织球墨铸铁的硬度