纯铁的同素异形结构及磁性特性

纯铁具有两种同素异形结构：体心立方体α—Fe、δ—Fe和面心立方体γ—Fe。在910℃以下时，纯铁呈α—Fe存在。在910℃时，体心立方晶格的α—Fe转变为面心立方晶格的γ—Fe，而γ—Fe在1400℃时又重新转变为体心立方晶格的α—Fe。不过，高温的α—Fe通常叫做δ—Fe。纯铁的物理性能和热力学数据见表3-1。下面讨论纯铁的热力学数据。

图3-1示出了纯铁比热与温度的关系，表3-1给出了具体的数值。一般来说，物质的比热随温度的升高而增高，这也就是说，当温度升高时，需要更多的热量才能使单位质量的物质升温1℃。比热与温度的关系可以用式（3-1）表示：

式中 CP——等压比热（cal^[1]/mol）；T——绝对温度；

a、b、c、d——系数。

又知等压比热可用式（3-2）计算：

式中 CV——等容比热（cal/mol）；

R——气体常数，R=1．987cal/mol。

纯铁发生的物理—化学过程，一般都是在恒压下进行的，所以应以CP 进行计算。但是另一方面，纯铁在固态和液态随温度而发生的体积变化又是很小的（dv≌0，dv为体积变化，以微分表示），因此，可以近似地认为CP≌CV。然而要指出的是，当温度非常高时，就会出现很大的偏差，因而CP≠CV。

由图3-1可以看出，在绝对温度为零度时，纯铁的CP值为零。随着温度升高，CP 值呈曲线增加，升温到760℃时达18cal/mol。在760℃ （居里点）时，α—Fe失去铁磁性。用虚线表示α—Fe到δ—Fe之间的过渡和它们之间的同一性。曲线的不连续性是与发生转变过程有关，而这都与晶格结构发生改变相联系。

图3-1　纯铁比热随温度的变化

表3-1　纯铁的物理性能和热力学数据

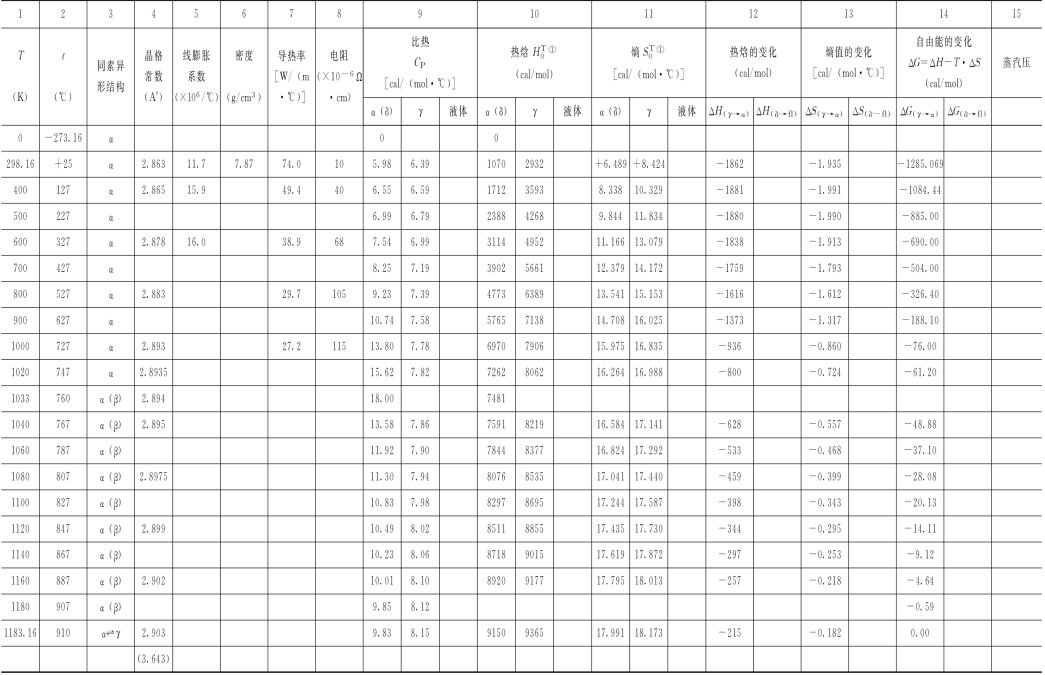
续表

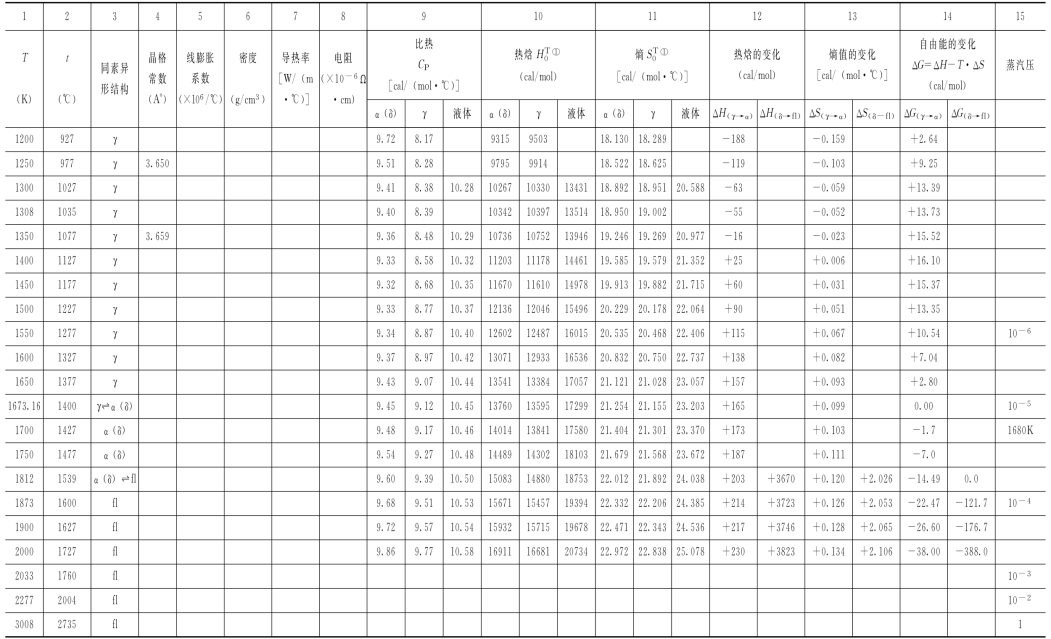
注表中12、13、14中的“fl ”指液体。
①取α—Fe 在绝对零点时的H0 *值为零。

图3-2　纯铁的热焓随温度的变化

根据热力学第一定律和热焓H的定义有式（3-3）：

由式（3-3）计算的纯铁热焓H0T 从绝对零度到绝对温度为2000K之间随温度变化的曲线关系示于图3 2。由于热焓没有绝对的度量值，所以必须建立初始点。正如图3-2所示，假定认为H0* （*指标准态，这里指的是纯铁，而且是指固态α—Fe；0指初始温度，这里指的是0K）等于零。由于在低温时测量热量值是很困难的，所以常常选择初始温度为298．16K=25℃。初始点的选择是任意的，但重要的是，在进行热力学计算时，必须选用相同的初始数据。

由图3-2得知，在曲线表示的转变点处有飞跃，这是因为任何一种同素异形转变均与能量发生变化相关，这些能量变化有相变热、熔化潜热、汽化热、升华热等。在计算热焓时，必须考虑这些参数。因此，铁液从零度到T温度的热焓用式（3-4）计算：

用式（3-4）计算得出的数据示于表3-1中的第10项。(www.xing528.com)

由热力学第二定律得式（3-5）：

式中 ΔG*——标准态自由能的变化；

R——气体常数；

T——绝对温度；

K——平衡常数。

由热力学第二定律得式（3-6）：

式中 ΔH*——标准态下的热焓变化；

ΔS*——标准态下的熵值变化。

对于纯铁来说，α—Fe和δ—Fe在1183K以下和在1673～1812K时的自由能要比γ—Fe的自由能小，而γ—Fe在1183～1673K时，则具有最小的自由能数值。表3-1中的第14项和在图3-3中示出了ΔG*值随温度的变化，该曲线在1183K和1673K两次通过零点。在这些零点处，ΔG*=0，这也就是说，此时转变处于平衡状态。

将式（3-5）代入式（3-6）中得式（3-7）：

令：

所以，

或：

由此，可以确定ΔH*和ΔS*。

如果用试验方法求出K 值与温度的关系，由此就可以确定ΔH*和ΔS*值。另外，如果ΔH*和ΔS*值为已知时，就可计算K值。

表3-1中除了纯铁的物理性能 （同素异形结构、晶格常数、线膨胀系数、密度、导热率和比热等）外，还给出了纯铁的热力学数据，其中包括热焓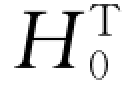、熵 及ΔH、ΔS值随温度的变化。

图3-3　α—Fe（δ—Fe）和δ—Fe的自由能随温度的变化