弧垂、线长及应力计算方法优化

1.弧垂、线长的计算

架空线由于档距很大，材料的刚性影响可以忽略不计，架空线的形状就像一条两端悬挂的柔软的索链，所以架空线可按悬链线计算其弧垂及线长。其计算式为

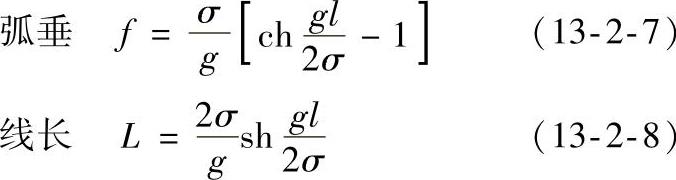
根据悬链线公式的级数形式展开，式（13-2-7）和式（13-2-8）又可写成级数形式。

或

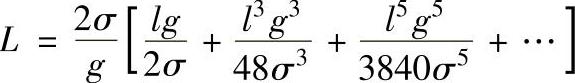
或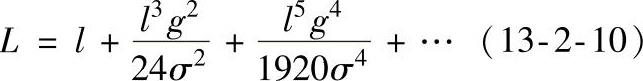

式中 l——档距（m）；

g——架空线的比载[N/（m·mm²）]，g=W/S；

W——单位长度导线的重量（N/m）；

S——导线截面积（mm²）；

σ——架空线的最低点应力（即水平应力）（N/mm²）。

为了简化计算，工程施工计算中仅取式（13-2-9）的第一项计算弧垂、取式（13-2-10）的前两项计算线长，即用抛物线方程代替悬链线方程近似计算，已能满足工程要求，即

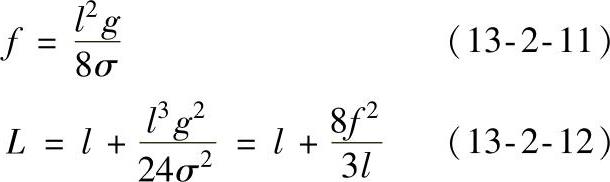
按上述抛物线方程代替悬链线方程计算，其误差是很小的。当弧垂不大于档距的5%时，线长误差率小于15×10^-4%。

在交叉跨越档距中，一般需计算被跨越物上面任一点导线的弧垂f_x，以便校验交叉跨越距离。如图13-2-9所示，档距中任一点导线弧垂按下式计算：

式中 x——从任一悬点至计算坐标点x的水平距离（m）。

图13-2-9 任一点的弧垂f_x示意图

悬挂点具有高差的档距中，架空线的计算需用斜抛物线法，即

式中 φ——高差角，。

2.应力计算和状态方程

架空线各点所受应力的方向是沿切线方向变化的，最低点处的应力称为水平应力，只要知道最低点应力，架空线上任何一点的应力都可用下式计算求得

σ_x=σ+（f-f_x）g （13-2-17）

式中 σ——架空线的水平应力（N/mm²）；

f——架空线的弧垂（m）；

f_x——计算点导线的弧垂（m）；

g——架空线比载[N/（m·mm²）]。

架空线的悬挂点应力则为

σ_A=σ+fg （13-2-18）(www.xing528.com)

当气象条件变化时，架空线所受温度和负荷也发生变化，其水平应力（简称应力）和弧垂也均随着变化，不同气象条件下的水平应力可根据状态方程式进行计算：

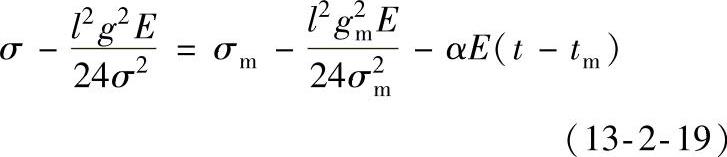
式中 σ_m——比载为g_m、气温为t_m时，架空线的水平应力（N/mm²）；

σ——比载为g、气温为t时，待求的架空线的水平应力（N/mm²）；

α——架空线的温度线膨胀系数（℃^-1）；

E——架空线的弹性模量（N/mm²）；

l——档距或孤立档档距（m）。

令：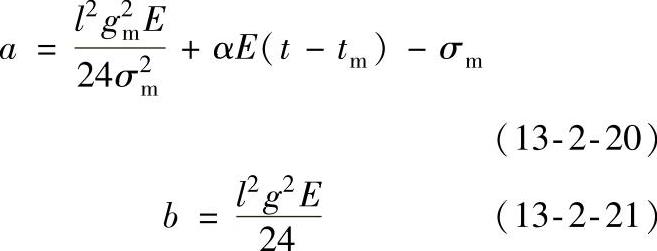

则式（13-2-19）变为

σ³+aσ²=b

或

σ²（σ+a）=b （13-2-22）

当已知某一气象条件（比载为g_m，气温为t_m）下的架空线应力为σ_m时，就可用上述状态方程求得另一气象条件（比载为g，气温为t）下的架空线应力σ。

为了保证架空线路安全，架空线的最大使用应力在任何情况下都要小于许用应力，即

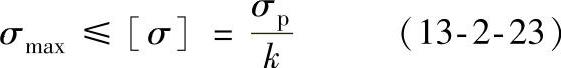
式中 σ_p——架空线的瞬时破坏应力（N/mm²）；

k——架空线的安全系数，设计安全系数不应小于2.5。

所以架空线最低点的应力可用式（13-2-19）状态方程式以许用应力作为架空线的最大使用应力及以出现最大应力的气象情况作为控制条件求得，即

式中 g_m——架空线出现最大应力时的气象条件下架空线的比载[N/（m·mm²）]；

t_m——架空线出现最大应力时的气温（℃）；

[σ]——架空线许用应力（N/mm²）。

这样在任何气象情况下的应力均不致超过规定强度的许用应力。

当求得某气象情况下的导线、地线应力后，则架空线弧垂最低点的拉力可按下式计算：

T₀=σ₀S

架空线任一点处的拉力为

T_x=σ_xS

式中 S——架空线截面积（mm²）。

3.弧垂曲线

架空线的安装架设是在不同气温下进行的，施工紧线时需要用事前做好的安装曲线（或安装表格），查出各种施工气温（无风无冰）下的弧垂，以确定架空线的松紧程度，使其在运行中任何气象条件下的应力都不超过最大使用应力，且满足耐振条件，使导线任何一点对地面、水面和被跨越物之间的距离符合设计要求，来保证运行的安全。

安装曲线通常只绘制弧垂曲线，绘制方法是以档距为横坐标，以弧垂为纵坐标，根据计算出来的各种施工气温下的弧垂数据绘制一套弧垂曲线。安装曲线上的弧垂是用抛物线公式计算的，而安装情况下的应力是根据架空线的最大使用应力和控制气象情况的比载和气温代入状态方程式中求得的。有时在安装曲线图上亦把安装应力曲线一并绘上，以便施工时查阅。安装曲线的绘制一般从最高施工气温至最低施工气温间每隔10℃（或5℃）绘制一条曲线，如图13-2-10所示。