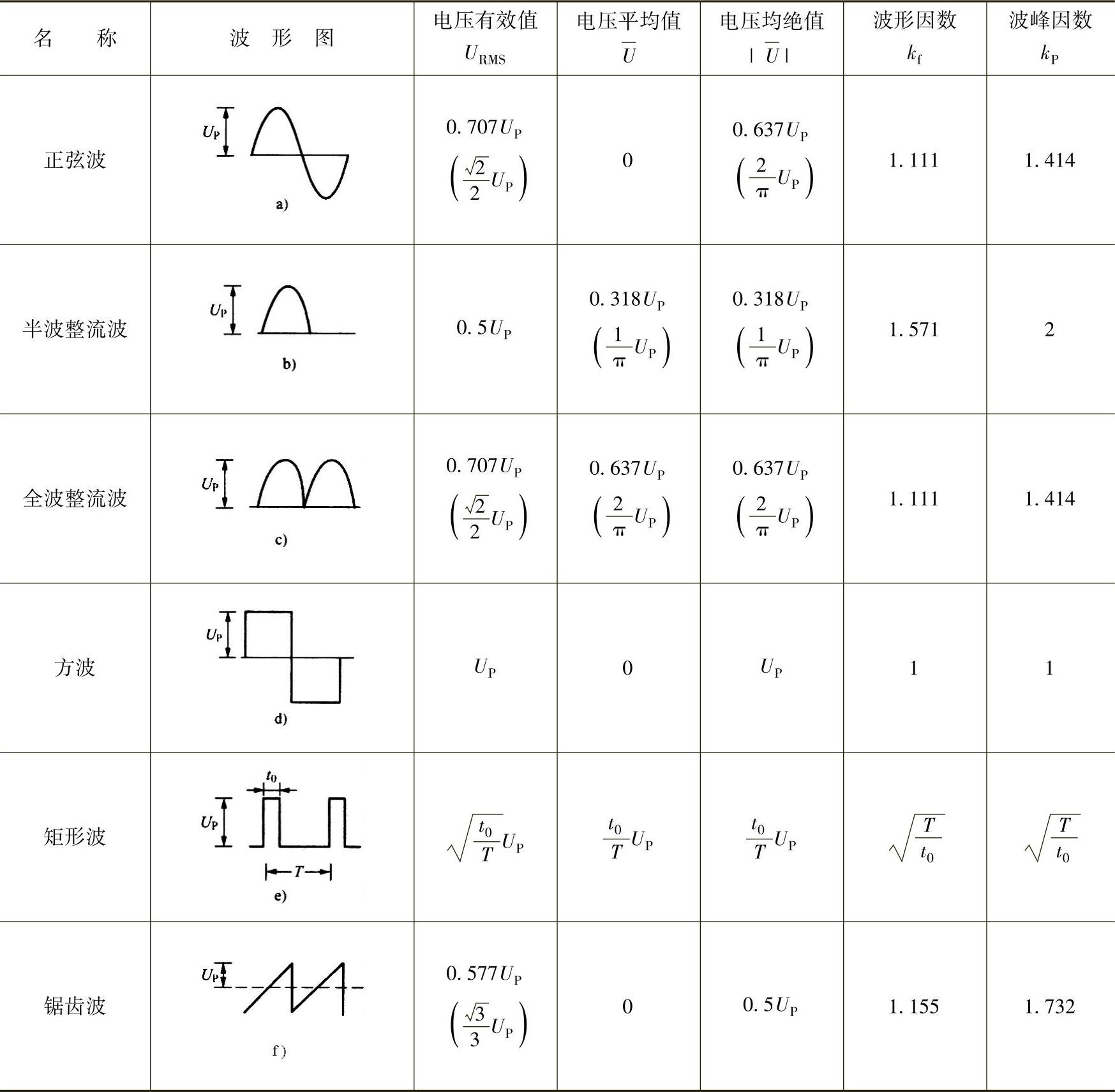
【摘要】:高频变压器电路中有3个波形参数:波形系数,波形因数,波峰因数。波形系数Kf为便于分析,在不考虑铜损的情况下给高频变压器的输入端施加交变的正弦波电流,在一次、二次绕组中就会产生感应电动势e。其中N为绕组匝数,A为变压器磁心的截面积,B为交变电流产生的磁感应强度,角频率ω=2πf。利用傅里叶级数不难求出方波的波形系数。因方波和梯形波的平均值为零,故改用电压均绝值来代替。表11-6 开关电源6种常见波形的参数
开关电源的电压及电流波形比较复杂,既有输入正弦波、半波或全波整流波,又有矩形波(PWM波形)、锯齿波(不连续电流模式的一次侧电流波形)、梯形波(连续电流模式的一次侧电流波形)等。高频变压器电路中有3个波形参数:波形系数(Kf),波形因数(kf),波峰因数(kP)。
(1)波形系数Kf
为便于分析,在不考虑铜损的情况下给高频变压器的输入端施加交变的正弦波电流,在一次、二次绕组中就会产生感应电动势e。根据法拉第电磁感应定律,e=dΦ/dt=d(NABsinωt)/dt=NABωcosωt。其中N为绕组匝数,A为变压器磁心的截面积,B为交变电流产生的磁感应强度,角频率ω=2πf。正弦波的电压有效值为
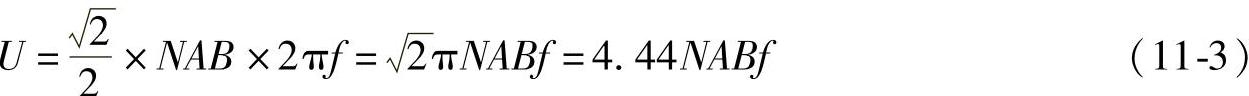
在开关电源中定义的正弦波波形系数Kf=2π=4.44。利用傅里叶级数不难求出方波的波形系数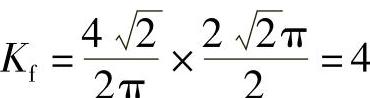 。
。
(2)波形因数kf
在电子测量领域定义的波形因数与开关电源波形系数的定义有所不同,它表示有效值电压(URMS)与平均值电压(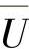 )之比,为便于和Kf区分,这里用小写的kf表示,有公式
)之比,为便于和Kf区分,这里用小写的kf表示,有公式
 (https://www.xing528.com)
(https://www.xing528.com)
与之相对应的波峰因数(kP)则定义为峰值电压(UP)与有效值电压之比,公式为

以正弦波为例,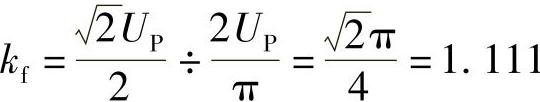 。这表明,Kf=4kf,二者恰好相差4倍。
。这表明,Kf=4kf,二者恰好相差4倍。
开关电源6种常见波形的参数见表11-6。因方波和梯形波的平均值为零,故改用电压均绝值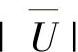 来代替。对于矩形波,t0表示脉冲宽度,T表示周期,占空比D=t0/T。
来代替。对于矩形波,t0表示脉冲宽度,T表示周期,占空比D=t0/T。
表11-6 开关电源6种常见波形的参数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




