立体半椭球的加工方法与技巧

图4-29所示的椭圆球参数尺寸如下：长轴半径为R10，短轴半径为R11，椭球高度为R12，试用参数方式编写半椭圆球通用子程序，并编写一个长轴半径为300mm，短轴半径为160mm，高度为80mm的半椭球加工程序。毛坯为实心的360mm×200mm×80mm的长方体材质为45钢。

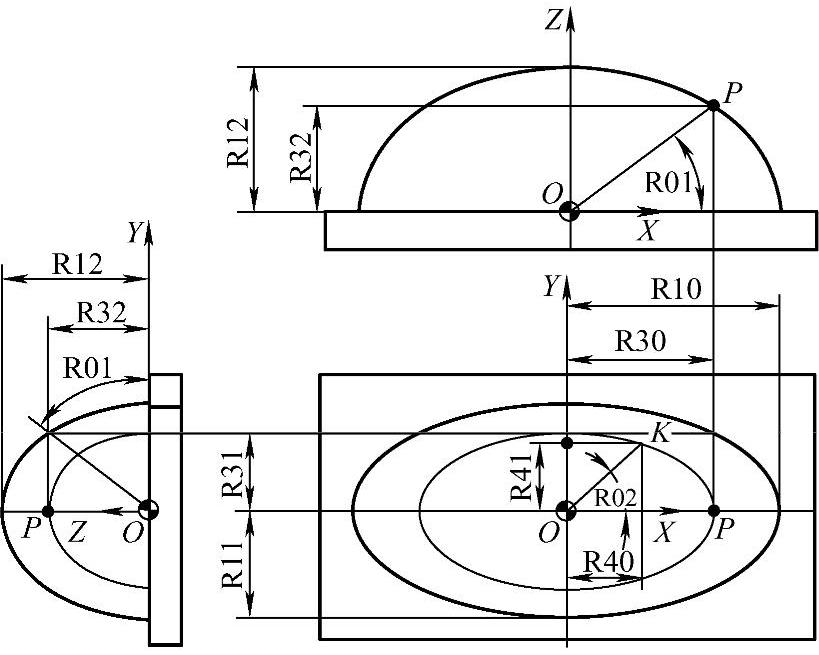
图4-29 任意立体半椭球的加工

1.工艺分析

以椭圆为母线的回转体椭圆球在车床上车削加工很容易，而现在的椭圆球零件，在任何一个轴上的截面均不是一个圆，因而是无法在车床上车削加工的。零件外形是立体半椭球的规则曲面，图中仅是半椭球要加工，表面粗糙度值按Ra3.2μm，其余为非加工表面，可预先在铣床上加工出工件的上、下表面及四周轮廓，以便加工椭圆轮廓时的装夹与找正。

工件装夹：选用机用虎钳装夹工件，找正机用虎钳固定钳口与工作台X轴移动方向平行在毛坯铣削完毕后，在工件下表面与机用虎钳之间放入厚度适当的平行垫块，工件装夹之前用表检测垫块表面平面度，工件露出钳口表面不低于椭球高度10mm，利用木锤或铜棒敲击工件，使平行垫块不能移动后，再夹紧工件。找正工件X轴、Y轴零点位于工件对称中心位置。工件上表面为执行刀具长度补偿后的Z零点表面，根据椭圆大小选用合适的平底键槽铣刀（粗加工）与球头铣刀（精加工）加工椭圆外形轮廓，至达到尺寸要求。铣刀半径设为R05采用刀心编程，轮廓尺寸加铣刀半径R05。

2.参数设定

为了程序能够通用，将立体半椭球的加工编写编制成R参数子程序，然后通过调用子程序的方式加工某一具体的立体半椭球，有关参数题中已给定，中间参数R01为椭球上任意点与椭球中心点的连线在垂直平面上与X轴的夹角；R02是连线在水平面上与X轴的夹角，如图4-29所示。

3.编程思路

与4.5节例1相似，要利用椭圆方程式X=acosβ，Y=bsinβ编写，不同之处在于本例是立体的椭球，用平行于坐标平面的平面去截取椭球，得到的截面均为椭圆，不同截平面所获得的椭圆方程式为X=acosβ，Y=bsinβ，其长半径a、短半径b是变化的，这就必须找出它们的变化规律来。如图4-29所示，P点为半椭球上的任意一点，过P点的水平截平面所截得的椭圆轮廓如图虚线所示，在主视图上是一条直线，另两个视图上的投影如细实线椭圆（或半椭圆）所示，通过变量R01求得不同水平截平面所截得的椭圆轮廓（图4-30），每一层的椭圆由变量R01控制，取值范围为0°～90°，同一层椭圆轮廓的任意位置是K点，K的位置由变量R02控制，取值范围为0°～360°。下面是椭球程序编制的关键：

1）分层及层数的循环与控制。

2）每层的加工循环与控制。

3）各轴的坐标计算。

4）加工方向的确定。

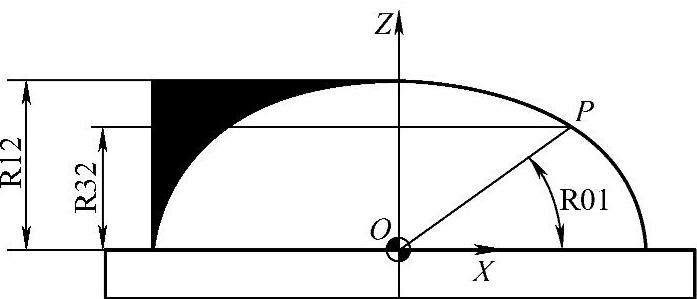
图4-30 椭球上P点椭圆截面层

由此可以看到，要用内外两层循环才能实现立体半椭球的程序编制，关于加工方向的确定分析：从图4-30中可以看出，无论是逐层向下还是逐层向上，加工余量都是不均匀的。经过粗加工，加工出半椭球的大体形状后，余量不均匀的情况会有所改善。采用逐层向下加工，开始加工的宽度余量较宽，需要较大直径的刀具；采用逐层向上加工，开始加工的深度余量较深，需要较大刃长的刀具，这就要根据椭球长、短径比来确定了。本例采用逐层向上加工的方法编写。(www.xing528.com)

4.立体半椭球参数子程序

程序如下：

5.调用立体半椭球参数子程序加工

如图4-31所示，半椭球的方程为：x²/50²+y²/25²+z²/35²=1，现调用半椭圆球参数子程序进行加工，主程序如下：

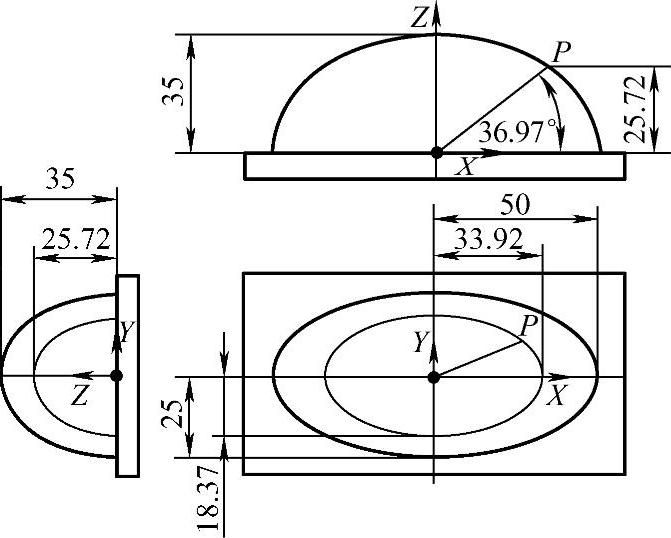
图4-31 半椭球加工

点评

以椭圆为母线的回转体椭球在车床上车削加工很容易，这是许多教科书上都能找的，也容易编程。本例中的立体半椭球用平行于坐标平面的平面去截取椭球，得到的截面均为椭圆，不同截平面所获得的椭圆方程式为x=a cosβ，y=b sinβ，其长半径a、短半径b是变化的，这就需要读者具有一定的空间想象力与空间解析几何等数学知识，如半椭球的方程为：x²/50²+y²/25²+z²/35²=1，这就是本例的难度所在。数控编程很具有代表性，许多立体方程曲面均可采用类似的编程方法，这就是本例的意义所在，应掌握的关键技术是：

1）分层及层数的循环与控制。

2）每层的加工循环与控制。

3）各轴的坐标计算。

4）加工方向的确定。