用编程实现任意正多边形

铣削任意正多边形的外轮廓，试编写出通用的R参数子程序。

1.图形设计

为了具有通用性，任意正多边形的边长要任意，边数要任意，正多边形中心位置要任意，且起始角度也要任意，加工用的刀具直径也要随任意正多边形的大小变化而变化，通过四个“任意”充分体现出正多边形的通用性！

任意正多边形的数控加工如图4-9所示。

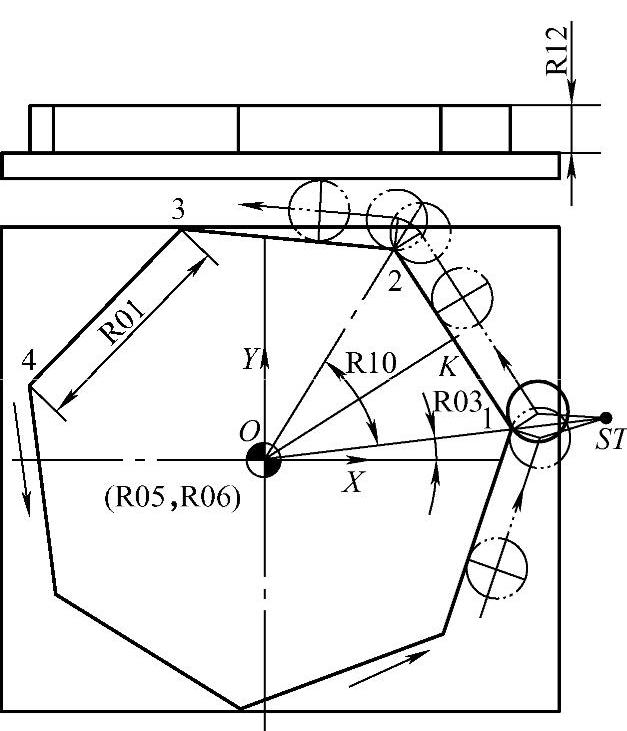
图4-9 任意正多边形的数控加工

2.相关参数设定与尺寸计算

正多边形边长=R01，正多边形边数=R02，起始位置角度=R03，正多边形中心点坐标设为（R05，R06），R10设为正多边形某一边对应的顶角，也是正多边形外接圆上的圆心角，根据上述已知条件可以计算出：R10=360/R02，正多边形中心点到各顶点的距离（即正多边形外接圆半径）R07=（R01/2）/SIN（R10/2）。

3.刀具选择

加工用的刀具直径也要随任意正多边形的大小变化而变化，为此，将刀具大小与边长建立联系，根据实际经验，取刀具半径为边长的1/10，且自动圆整并规定其最小半径与最大半径的范围，刀具半径R11=DIV（R01/10），起刀点ST的规定：从正多边形中心点开始加上边长再加上三倍刀具半径所确定的坐标点作为程序起点，加工结束后再回到ST点。

4.坐标计算

坐标计算有很多方法，如直角坐标系、极坐标系等。本例若采用直角坐标系计算，会很不方便。正多边形一定有一个外接圆，且每边所对应的圆心角相等，若采用极坐标系计算，因为各点的极心不变，极半径不变，且极角又有规律可循，再利用循环指令编程，那就方便多了。本例采用极坐标系加循环指令编程的方法。

已知条件：正多边形边长=R01，正多边形边数=R02，起始位置角度=R03，正多边形中心点坐标为（R05，R06），刀具半径R11=ROUND（R01/10）；在直角△KOI中，正多边形外接圆半径R07=（R01/2）/SIN（180/R02）；ST点：极半径值=R01+3*R11，极角=R03；每边所对应的圆心角，R10=360/R02；第1顶点坐标：极半径值=R01，极角=R03；第2顶点坐标极半径值=R01，极角=R03+R10。(www.xing528.com)

以后每个顶点的极角增加一个R12，而极半径值不变，当累计增加的角度值等于360°时，正多边形加工结束，这就是循环的终止条件。

5.程序编制

程序如下：

本例中的任意正多边形编程思路高度体现了“智能化”的编程思想，具体表现为：

1）正多边形的边长任意，边数任意，且起始角度任意。

2）正多边形中心点坐标任意。

3）加工用的刀具大小直径大小随任意正多边形的大小变化而变化。

4）起刀点位置也随任意正多边形的大小变化而变化，“智能化”走到起点位置。

上述的几个“任意”不仅体现了任意正多边形R参数子程序的通用性，更体现了按正多边形大小选择刀具直径大小、确定刀具起点位置的智能化以及操作机床的方便性与安全性等。

点评

数控机床朝着高性能、高精度、高速度、高柔性化和模块化方向发展，但最主要的发展趋势是智能化、开放化、网络化。其中的智能化发展趋势不外乎有两个方面：一是数控技术的开发者开发出更好的数控系统软件，二是数控技术的使用者利用数控系统软件编写出更好的数控加工程序。这里的数控技术使用者主要是编程人员，其编写的程序更能替机床操作者着想，减少操作步骤，做到人性化提示、方便与安全，就是真正的智能化体现。要让数控机床的操作者操作机床就像使用傻瓜相机一样的方便与简单，当然，还有很长的路要走。