风能资源的统计计算方法总结

（一）风况

1.年平均风速

年平均风速是一年中各次观测的风速之和除以观测次数，它是最直观简单地表示风能大小的指标之一。

我国建设风电场时，一般要求当地在10m高处的年平均风速在6m/s左右，这时，风功率密度在200～250W/m2，相当于风力发电机组满功率运行的时间在2000～2500h，从经济分析来看是有益的。

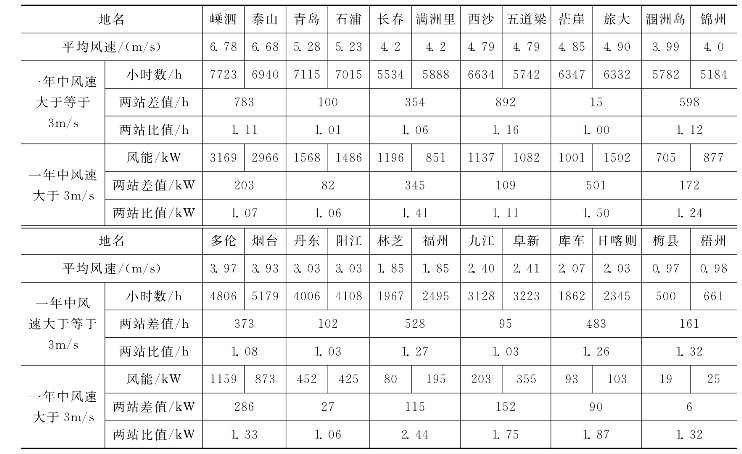
但是用年平均风速来要求也存在着一定的缺点，它没有包含空气密度和风频在内，所以年平均风速即使相同，其风速概率分布型式p（v）并不一定相同，计算出的可利用风能小时数和风能有很大的差异，见表1-1-10。可以看出，在平均风速基本相同的情况下，一年中风速大于等于3m/s在一年中出现的小时数，最大的可相差几百小时，占一年中风速大于等于3m/s出现小时数的30%，两者相等的几乎没有；其能量值相差就更为突出，有的可以相差1.5倍以上。从全国300余站资料的分析来看，情况大体相似，两站平均风速基本相同，其一年中风速大于等于3m/s的小时数和风能却不相同，若以相差5%为相同者，其站数还不到总站数的5%。

表1-1-10　各地风速、风能对比表

一般是春季风速大，夏秋季风速小。这有利于风电和水电互补，也可以将风力发电机组的检修时间安排在风速最小的月份。同时，风速年变化曲线与电网年负荷曲线对比，一致或接近的部分越多越理想。

2.风速日变化

风速虽瞬息万变，但如果把长时间的资料平均起来便会显出一个趋势。一般说来，风速日变化有陆、海两种基本类型：①陆地，白天午后风速大，夜间风速小，因为午后地面最热，上下对流最旺，高空大风的动量下传也最多；②海洋，白天风速小，夜间风速大，这是由于白天大气层的稳定度大，因为白天海面气温比海温高所致。

风速日变化与电网的日负载曲线特性相一致时，也是最好的。

3.风速随高度变化

在近地层中，风速随高度有显著的变化，造成风在近地层中的垂直变化的原因有动力因素和热力因素，前者主要来源于地面的摩擦效应，即地面的粗糙度；后者主要表现与近地层大气垂直稳定度的关系。当大气层结为中性时，乱流将完全依靠动力发展，这时风速随高度变化服从普朗特经验公式，即

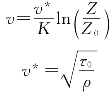
式中　v——风速，m/s；

K——卡曼常数，其值为0.4左右；

v＊——摩擦速度，m/s；

ρ——空气密度，kg/m3，一般ρ=1.225kg/m3；

τ0——地面剪切应力，N/m2；

Z——离地高度，m；

Z0——粗糙度，m。

经过推导可以得出幂定律公式为

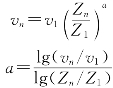
式中　vn——Zn高度处风速，m/s.

v1——Z1高度处风速，m/s；

a——为风切变指数。

如果没有不同高度的实测风速数据，风切变指数a取1/s（0.143）作为近似值，这相当地面为短草。在广州电视塔观测a为0.22，上海南京路电视塔为0.21，武汉跨江铁塔为0.19，北京八达岭风电试验站为0.19。

风速垂直变化取决于a值。a值的大小反映风速随高度增加的快慢，a值大表示风速随高度增加得快，即风速梯度大；a值小表示风速随高度增加得慢，即风速梯度小。

a值的变化与地面粗糙度有关，地面粗糙度是随地面的粗糙程度变化的常数，不同地面粗糙度风速随高度变化差异很大。粗糙的表面比光滑表面更易在近地层的垂直混合更为充分，混合作用的加强使得近地层风速梯度减小，所以粗糙的地面比光滑地面的风速小。

4.风向频率玫瑰图

风向频率玫瑰图可以确定主导风向，对于风电场机组位置排列具有关键作用，因为机组排列是垂直于主导风向的。

5.湍流强度

湍流是指风速、风向及其垂直分布的迅速扰动或不规律性，是重要的风况特征。湍流很大程度上取决于环境的粗糙度、地层稳定性和障碍物湍流强度，是脉动风速的均方差σ与平均风速的比值，即

Ir≤0.10时表示湍流较小，Ir≥0.25表示湍流过大，一般海上Ir=0.08～0.10，陆地上Ir=0.12～0.15。它有两种不利的影响，减少输出功率和引起风能转换系统的振动和荷载的不均匀，最终使风力发电机组受到破坏。

（二）风功率密度

1.风能

风能是空气运动的动能，或每秒在面积F上从以速度v自由流动所获得的能量，即获得的功率w。它等于面积、速度、气流动压的乘积，即

式中　ρ——空气密度，kg/m3；

w——风能，W；

v——风速，m/s；

F——面积，m2。

实际上，同一个地点空气密度为常数，当面积一定时，则风速是决定风能多少的关键因素。

风功率密度是气流垂直通过单位面积（风轮面积）的风能。它是表征一个地方风能多少的指标。因此在与风能公式相同的情况下，将风轮面积定为1m2（F=1m2）时，风能具有的功率为

衡量一地风能的大小，要视常年平均风能的多少而定。由于风速是一个随机性很大的变量，必须通过一定长度的时间观测来了解它的平均状况。因此，在一段时间（如一年）长度内风功率密度可以将上式对时间积分后平均，即

式中　——平均风能，W；

T——总时数，h。

由时间T内风速v的概率分布p（v）可计算出平均风功率密度。

在研究了风速的统计特性后，风速分布p（v）可以用一定的概率分布形式来拟合，这样就大大简化了计算的过程。

2.空气密度

从风能公式可知，ρ的大小直接关系到风能的多少，特别是在高海拔的地区，影响更为突出。所以，计算一个地点的风功率密度，需要掌握的量是所计算时间区间内的空气密度和风速。在近地层中，空气密度ρ的量级为100，而风速v3的量级为102～103。另一方面，由于我国地形复杂，空气密度的影响也必须要加以考虑。空气密度是ρ气压、气温和温度的函数，其计算公式为

式中　ρ——气压，hPa；

t——气温，℃；

e——水汽压，hPa。

3.风速的统计特性

由于风的随机性很大，因此在判断一个地方的风况时，必须依靠各地区风的统计特性。在风能利用中，反映风的统计特性的一个重要形式是风速的频率分布，长期观察的结果表明，年度风速频率分布曲线最有代表性。为此，应该具有风速的连续记录，并且资料的长度至少有3年以上的观测记录，一般要求能达到5～10年。

风速频率分布一般为偏态，要想描述这样一个分布至少要有3个参数，即平均风速、频率离差系数和偏差系数。关于风速的分布，国外有过不少的研究，近年来国内也有探讨。风速分布一般均为正偏态分布，一般说，风力越大的地区，分布曲线越平缓，峰值降低右移。这说明风力大的地区，一般大风速所占比例也多。如前所述，由于地理、气候特点的不同，各种风速所占的比例有所不同。

通常用于拟合风速分布的线形很多，有瑞利分布、对数正态分布、Γ分布、双参数威布尔分布、三参数威布尔分布等，也可用皮尔逊曲线进行拟合。但普遍认为双参数威布尔分布曲线是适用于风速统计描述的概率密度函数。

威布尔分布是一种单峰的，两参数的分布函数簇。其概率密度函数可表达为

式中　k、c——威布尔分布的两个参数；

k——形状参数；

c——尺度参数。

当c=1时，称为标准威布尔分布。形状参数k的改变对分布曲线形式有很大影响。当0＜k＜1时，分布的众数为0，分布密度为x的减函数；当k=1时，分布呈指数形；k=2时，便成为瑞利分布；k=3.5时，威布尔分布实际已很接近于正态分布了。

估计风速的威布尔分布参数有多种方法，依不同的风速统计资料进行选择。通常采用方法有三种：①最小二乘法，即累积分布函数拟合威布尔分布曲线法；②平均风速和标准差估计法；③平均风速和最大风速估计法。根据国内外大量验算结果，上述方法中最小二乘法误差最大。在具体使用当中，前两种方法需要有完整的风速观测资料，需要进行大量的统计工作；后一种方法中的平均风速和最大风速可以从常规气象资料获得，因此，这种方法较前两种方法有优越性。

4.平均风功率密度

根据式可知，w为ρ和v两个随机变量的函数，对一地而言，空气密度ρ的变化可忽略不计，因此，w的变化主要是由v3随机变化所决定，这样w的概率密度分布只决定风速的概率分布特征，即

风速立方的数学期望为

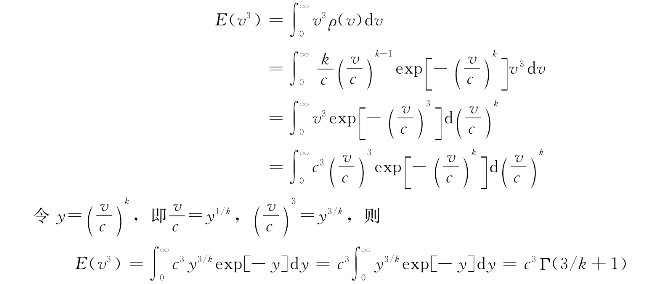
可见，风速立方的分布仍然是一个双参数威布尔分布，只不过它的形状参数变为3/k，尺度参数为c3。因此，只要确定了风速的双参数威布尔分布的参数c和k，风速的立方的平均值便可确定，平均风能密度为

5.参数c和k的估计

用即最小二乘法、平均风速和标准差估计威布尔参数方法、平均风速和最大风速估计威布尔分布参数的方法说明如下：

（1）用最小二乘法估计威布尔参数。根据风速的威布尔分布，风速小于vg的累积概率（分布函数）为

取对数整理后，有

(www.xing528.com)

令y=ln｛-ln［1-p（v≤vg）］｝，x=lnvg，a=-klnc，b=k，于是参数k和c可以由最小二乘法拟合y=a+bx得到。将观测到的风速出现范围划分成n个风速间隔：0～v1、v1～v2、…、vn-1～vn。统计每个间隔中风速观测值出现的频率f1、f2、…、fn和累积频率p1=f1、p2=p1+f2、…、pn=pn-1+fn。取下列变换

并令

因此，根据以上式子及上述风速累积频率观测资料，便可得到a、b的最小二乘估计值为

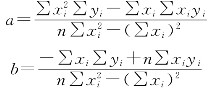
由上可得

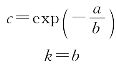
（2）根据平均风速v和标准差si估计威布尔分布参数。

可见仅仅是k的函数。因此当知道了分布的均值和方差拌便可求解k。由于直接用求解k比较困难，因此通常可用上式的近似关系式求解k为

因而得出

以平均风速估计μ，样本标准差sv估计σ，即

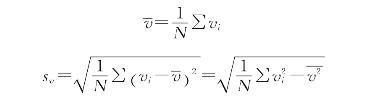
式中　vi——计算时段中每次的风速观测值，m/s；

N——观测总次数。

由上式便可求得k和c的估计值。在各个等级风速区间（如0、1m/s、2m/s、3m/s、…、m/s）的频数已知的情况下，v和sv可以近似地计算如下

式中　vj——各风速间隔的值，m/s，以该间隔中值代表该间隔平均值；

nj——各间隔的出现频数。

（3）用平均风速和最大风速估计威布尔分布参数。我国气象观测规范规定，最大风速的挑选指的是一日任意时间的10min最大风速值。设vmax为时间T内观测到的10min平均最大风速，显然它出现的概率为

对上式逆变换得

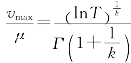
因此在知道了vmax和后，以作为μ的估计值，由上式就可能解出k。直接计算比较麻烦，而大量的观测表明，k值通常变动范围为1.0～2.6之间。此时，于是得k的近似解为

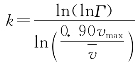
进而求得

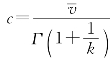
考虑到vmax的抽样随机性很大，又有较大的年际变化，为了减小抽样随机性误差，在估计一地的平均风能潜力时，应根据v和vmax的多年平均值（最好10年以上）来估计风速的威尔分布参数，有较好的代表性。

6.有效风功率密度

在有效风速范围（风力发电机组切入风速到切出风速之间的范围）内，设风速分布为p′（v），风速立方的数学期望为

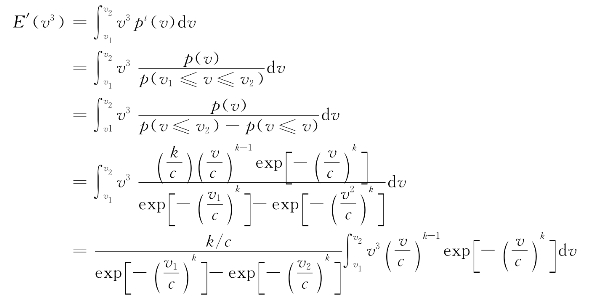
上式可通过数值积分求得。因此有效风能密度便可计算出来，即

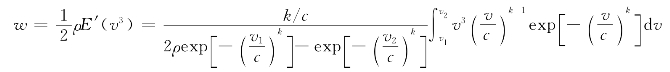
确定了风速的威布尔分布两个参数c和k之后，在工作风速风，切入风速v1到切出风速v2，其有效平均风能密度的计算为

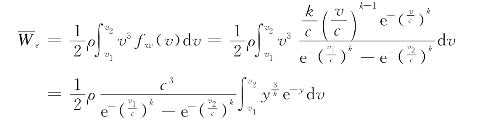
式中，，积分号下为不完全Γ函数，可以通过数值积分求得。

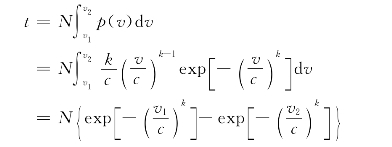
式中　N——统计时段的总时间，h；

v1——风力发电机组的启动风速，m/s；

v2——风力发电机组的停机风速，m/s。

一般年风能可利用时间在2000h以上时，可视为风能可利用区。

确定了风速的威布尔分布两个参数c和k之后，风能可利用时间t，即时段N内出现有效风速（v1≤v≤v2）的小时数为

7.风能可利用时间

在风速概率分布确定以后，还可以计算风能的可利用时间。

只要给定了威布尔分布参数c和k之后，平均风功率密度、有效风功率密度、风能可利用小时数都可以方便地求得。另外，知道了分布参数c、k，风速的分布型式便给定了，具体风力发电机组设计的各个参数同样可以加以决定，而无须逐一查阅和重新统计所有的风速观测资料，它无疑给实际使用带来许多方便。一些研究结果还表明，威布尔分布不仅可用于拟合地面风速分布，也可用于拟合高层风速分布。其参数在近地层中随高度的变化很有规律。当知道了一个高度风速的威布尔分布参数，便不难根据这种规律求出近地层中任意高度风速的威布尔分布参数。

（三）风功能密度等级及风能可利用区的划分

风功率密度等级蕴涵着风速、风速频率分布和空气密度的影响，是衡量风电场风能资源的综合指标。风功率密度等级在国标“风电场风能资源评估方法”中给出了7个级别，见表1-1-11。

表1-1-11　风功率密度等级表

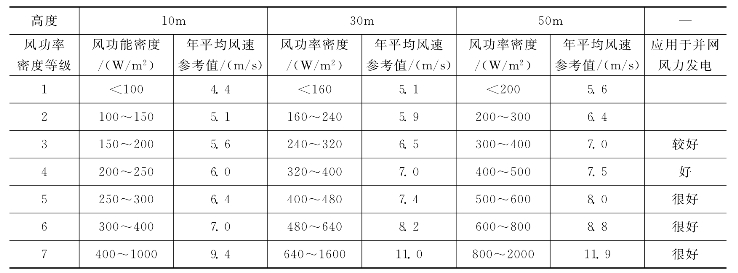
注　1.不同高度的年平均风速参考值是按风切变指数为1/7推算的。
2.与风功率密度上限值对应的年平均风速参考值，按海平面标准大气压并符合瑞利风速频率分布的情况推算的。

由表1-1-11可以看出当风功率密度大于150W/m2、年平均风速大于5m/s的区域被认为是风能资源可利用区；10m高处年平均风速在6m/s，风功率密度为200～250W/m2为较好的风电场；年平均风速为7m/s，风功率度为300～400W/m2为很好的风电场。

一般说平均风速越大，风功率密度也大，风能可利用小时数就越多。我国风能区域等级划分的标准如下：

（1）风能资源丰富区。年有效风功率密度大于200W/m2，3～20m/s风速的年累积小时数大于5000h，年平均风速大于m/s。

（2）风能资源次丰富区。年有效风功率密度为200～150W/m2，3～20m/s。风速的年累积小时数为5000～4000h，年平均风速在5.5m/s左右。

（3）风能资源可利用区。年有效风功率密度为150～100W/m2如，3～20m/s风速的年累积小时数为4000～2000h，年平均风速在5m/s左右。

（4）风能资源贫乏区。年有效风功率密度小于100W/m2，3～20m/s风速的年累积小时数小于2000h，年平均风速小于4.5m/s。

风能资源丰富区和较丰富区具有较好的风能资源，为理想的风电场建设区。

风能资源可利用区，有效风功率密度较低，这对电能紧缺地区还是有相当的利用价值。实际上，较低的年有效风功率密度也只是对宏观的大区域而言，而在大区域内，由于特殊地形有可能存在局部的小区域大风区，因此，应具体问题具体分析。通过对这种地区进行精确的风能资源测量，详细了解分析实际情况，选出最佳区域建设风电场，效益还是相当可观的。

风能资源贫乏区，风功率密度很低，对大型并网型风电机组一般无利用价值。

（四）风能资源的评估

风能资源多少是风能利用的关键。收集能量的成本是由风电机组设备的成本、安装费用和维修费等与实际的生产能量所确定的。因此，不但要着重考虑节省基本投资，而且要根据当地风能资源选择适当的风电机组，使风电机组与风能资源两者相匹配，才能获得最大的经济效益。

根据风的气候特点，较长时间的观测资料才有较好的代表性。一般说来，需要有10年以上的观测资料才能比较客观地反映一地的真实状况。为此，计算了全国900余个气象台站10年平均风能密度值，绘制成全国年平均风功率密度分布图。利用图上的10W/m2、25W/m2、50W/m2、100W/m2、200W/m2和大于2000W/m2的各风功率密度等值线间的面积，然后分别乘以各等级风功率密度的代表值。

由于考虑一个单位截面积的风能转换装置，风吹过后必须经前后左右各10倍直径距离后才能恢复到原来的速度，所以将各等级风功率密度等值线的面积的总和除以100，即可得到风能总储量。

据测算，在10m高处我国风能理论资源储量约为32.0亿kW，实际可供开发的量按32.0亿kW的1/10估计，则可开发量为3.2亿kW。考虑到风电机组风轮的实际扫掠面积为圆形，对于1m直径风轮的面积为0.52π=0.785m2。因此，再乘以面积系数0.785，即为经济可开发量。由此，得到全国风能经济可开发量为2.53×1010W，即2.53亿kW。

（五）风能资源的分区

根据全国有效风功率密度和一年中风速大于等于3m/s时间的全年累积小时数，可以看出我国风能资源的地理分区。

（1）东南沿海及其岛屿为我国最大风能资源区。有效风功率密度大于等于200W/m2的等值线平行于海岸线，沿海岛屿的风功率密度在300W/m2以上，一年中风速大于等于3m/s的时数为7000～8000h。但从这一地区向内陆则丘陵连绵，冬半年强大冷空气南下，很难长驱直下，夏半年台风在离海岸50km，风速便减少到68%。所以东南沿海仅在山海岸向内陆几十千米的地方有较大的风能，再向内陆风能锐减，在不到100km的地带，风功率密度降至50W/m2以下，反为全国最小区。但在沿海的岛屿上（如福建台山、平潭等，浙江南鹿、大陈，嵊泗等广东的南澳）风能都很大。其中台山风功率密度为534.4W/m2，一年中风速大于等于3m/s的时数累计出现7905h。换言之，平均每天一年中风速大于等于3m/s的时数有21h20min，它是我国平地上有记录的风能资源最大的地方之一。

（2）内蒙古和甘肃北部以北广大地带为次大区。这一带终年在高空西风带控制之下，且又是冷空气入侵首当其冲的地方，风功率密度在200～300W/m2，一年中风速大于等于3m/s的时间全年有5000h以上，从北向南逐渐减少，但不像东南沿海梯度那样大。最大的虎勒盖地区，一年中风速大于等于3m/s的时间累积时数可达7659h。这一区虽较东南沿海岛屿上的风功率密度小一些，但其分布的范围较大，是我国连成一片的最大地带。

（3）黑龙江和吉林东部及辽东半岛沿海风能也较大，风功率密度在200W/m2以上，一年中风速大于等于3m/s的时数也达5000～7000h。

（4）青藏高原北部风功率密度在150～200W/m2之间，一年中风速大于等于3m/s可达6500h，但由于青藏高原海拔高，空气密度较小，所以风功率密度相对较小，在4000m的空气密度大致为地面的67%。也就是说，同样是8m/s的风速，在平地为31306W/m2，而在4000m只有209.9W/m2。所以，若仅按一年中风速大于等于3m/s的时数，青藏高原应属风能最大区，实际上这里的风能远较东南沿海为小。

（5）云南、贵州、四川，甘肃、陕西南部、河南、湖南西部以及福建、广东、广西的山区，西藏、雅鲁藏布江以及新疆塔里木盆地为我国最小风能区，有效风功率密度在50W/m2以下，一年中风速大于等于3m/s的时数在2000h以下。在这一地区，尤以四川盆地和西双版纳地区风能最小，这里全年静风频率在60%以上，如绵阳67%、巴中60%、阿坍67%、恩施75%、德格63%、耿马孟定72%、景洪79%，一年中风速大于等于3m/s的时数仅有300多h，所以这一地区除高山顶和峡谷等特殊地形外，风力潜能很低，无利用价值。

（6）在（4）和（5）地区以外的广大地区为风能季节利用区。如有的在冬季、春季可以利用，有的在夏秋可以利用等，这一地区风功率密度在50～150W/m2之间，一年中风速大于等于3m/s的时数为2000～4000h。表1-1-12给出了我国风资源可开发量和经济可开发量。

表1-1-12　中国各省（自治区）风能储量

续表

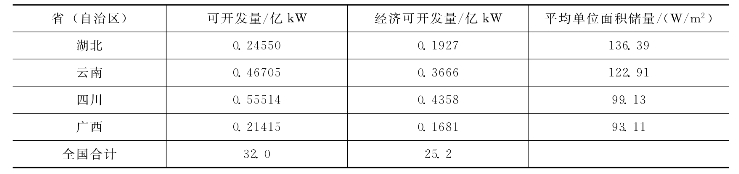
必须说明，上述的资源储量不包括近海的储量，根据不完整的资源估算，近海（水深10m），离海面10m高，风能储量约为陆地的3倍，即约7.5亿kW。