（1）试论述金属塑性成形方法的特点。
（2）选择日常所见的机械或零件，试分析一下它所采用的加工方法。如果认为是塑性加工件，能否分析一下其所用成形方法。
（3）考虑表1-1所示的圆棒拉拔和正挤压工艺，为什么它们的应变状态相同，但应力状态各不相同？
（4）说明实际金属晶体结构中常见缺陷。
（5）单晶体中塑性变形时沿什么样的晶面和晶向容易发生滑移？说明原因。
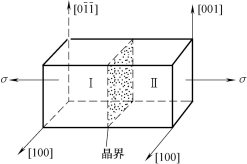
题图1 简单立方结构的双晶体
（6）假设有一简单立方结构的双晶体，如题图1所示，如果该金属的滑移系是{100}<100>，问在正应力σ作用下，该双晶体中的哪一个晶体首先发生滑移？为什么？
（7）简述滑移与孪生变形机制的异同。
（8）单晶体在拉伸和压缩变形时，滑移面分别是怎样转向的？用图示说明。
（9）多晶体的塑性变形有哪几种方式？有什么特点？
（10）试用位错理论说明晶体滑移的机制。
（11）什么是加工硬化？说明其产生原因及利弊？
（12）什么是“制耳”现象？说明其产生的原因。
（13）说明影响金属材料塑性的因素有哪些？
（14）说明静态回复的温度、机制及在生产上的应用。
（15）什么是二次再结晶？什么条件下容易发生？
（16）根据加工温度的不同，金属的塑性变形方法有哪3种？其应用情况如何？
（17）什么是塑性？常见的塑性指标有哪些？为何说塑性指标只有相对意义？
（18）说明轧制试验法测试金属塑性的过程，其特点是什么？
（19）简要说明碳素钢的化学成分及其对塑性的影响。
（20）说明晶粒大小对塑性的影响机制。
（21）简述变形温度对金属塑性的影响。
（22）什么是热效应和温度效应？其对塑性变形有什么影响？
（23）简述变形程度对金属塑性的影响。
（24）为什么说应力状态对塑性影响的实质是静水压力的影响？
（25）说明改善金属塑性的对策。
（26）什么是金属的超塑性？其变形特点如何？
（27）超塑变形与普通塑性变形的力学特性有何异同？
（28）超塑变形分为哪几类？各自有什么特点？
（29）简述超塑变形的应用情况。
（30）简述超塑变形的机制。
（31）如何完整地表示受力物体内任一点的应力状态和应变状态，并说明原因。
（32）已知oxyz坐标系中物体内某点的应力坐标为（4，3，-12），其应力分量为
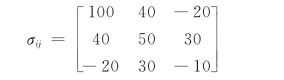
①将应力分量画在单元体上；
②求出通过该点且方程为x+3y+z=1的平面上的正应力和剪应力；
③求出其主应力，主轴方向，主剪应力，最大剪应力，应力偏张量及球张量，八面体应力和等效应力；
④现将直角坐标系改成圆柱坐标系，原点不变，取原x轴为极轴，试求其应力分量σlk（l，k=ρ，θ，z），并判断它是否是轴对称状态（提示：σlk也就是原坐标系中ρ，θ，z方向各微分面上的应力分量）。
（33）设某物体内的应力场为
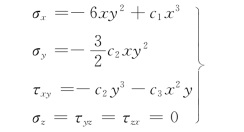
试求系数c1，c2，c3（提示：应力场必须满足平衡方程）。
（34）题图2为圆锥形模具的正挤压。冲头P以
=-1m/s的速度向左推移。假设，材料不可压缩，变形区限制在a-a及b-b线之间的锥台区内，区内各质点的速度矢量都指向锥顶点O，而且所有垂直于z轴的平面上的z向速度分量均布。
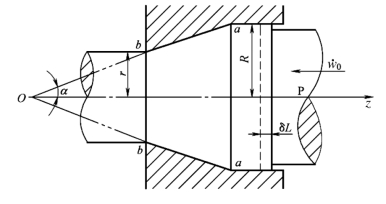
题图2 圆锥形模具的正挤压
试求：①变形区内的速度场和应变速率场；
②在某时刻后10-4s时间之内的位移场及应变场。
（35）试判断下列应变场能否存在：
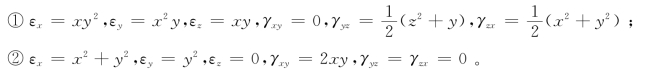
（36）已知平面应变状态下，变形体某点的位移函数为
，试求该点的应变分量εx，εy，γxy，并求出主应变ε1，ε2的大小与方向。
（37）设一试棒均匀连续拉伸5次，每拉一次断面收缩20%，试用相对伸长、断面收缩率和对数应变分别求出各次的应变值和总应变值。并分析一下哪一种应变表达式比较合理。
（38）常用的屈服准则有哪两个？各有什么物理意义？分别写出其数学表达式。
（39）两个屈服准则有何差别？在什么状态下两个屈服准则相同？什么状态下差别最大？
（40）如用纯剪应力状态，也即薄壁管扭转试验来确定屈服准则中的常数C，在试验中得到屈服时剪应力为K，试写出屈雷斯加和米塞斯准则的表达式。
（41）已知平面变形时，式（17-15）中的系数β=1.155，单向应力及某些轴对称状态时β=1。试分析平面应力时β是否有确定的值。
（42）一直径为50mm的圆柱形试样在无摩擦的光滑平板间镦粗，当总压力达到314kN时试样屈服。现设在圆柱体周围加上1 000N/cm2的静水压力，试求试样屈服时所需的总压力。
（43）一薄壁管，内径80mm，壁厚4mm，承受内压p，材料的屈服应力为200N/mm2，假定管壁上的径向应力σr=0。试用屈雷斯加和米塞斯屈服准则分别求出下列情况下管子屈服时的p：(www.xing528.com)
①管子两端自由；②两端封闭；③两端不封闭且加100kN的压力。
（44）试判断下列应力状态是使材料处于弹性状态还是处于塑性状态？
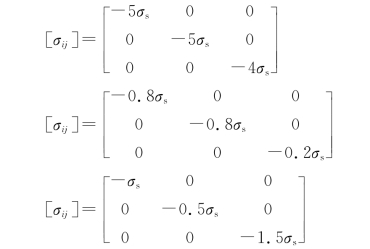
（45）有一方断面梁，边长为A，且是理想弹塑性材料，屈服应力为σs，承受纯弯曲。试求：①该梁上下表面层进入塑性状态时的弯矩为Mcl；②该梁全部断面都进入塑性状态时的弯矩Mpl；③如果弯矩大于Mpl，会产生什么现象？
（46）题图3所示的薄壁圆管受拉力F和扭矩M的作用而屈服，试写出此情况下的米塞斯屈服准则和屈雷斯加屈服准则的表达式。
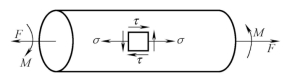
题图3 薄壁圆管受力示意图
（47）
为应力偏量，试证明用应力偏量表示米塞斯屈服条件时，其形式为
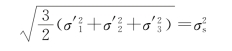
（提示
=0）
（48）试用应力的第一、第二不变量Jl、J2来表示米塞斯屈服条件。
（49）证明应力分量
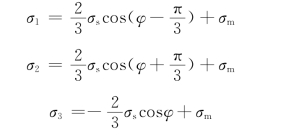
恒满足米塞斯条件，又当σ1≥σ2≥σ3时，对φ有什么限制？
（50）已知二端封闭的薄壁圆筒，半径为r，厚度为t，受内压p及轴向拉应力σ的作用，试求此时圆筒的屈服条件，并在p—σ平面上画出屈服轨迹。
（51）已知半径为50mm，厚为3mm的薄壁圆管，保持
，材料拉伸屈服极限为400MPa，试求此圆管屈服时轴向载荷P和扭矩Ms。
（52）已知薄壁圆球，其半径为r0，厚度为t0，受内压p的作用，试求使用屈雷斯加条件时，p值为多少时发生屈服？
（53）将米塞斯条件用主应力写出，并研究两种特殊情况：①σ1=σ2和②σ2=σs，将这两种特殊情况中所写出的屈服条件与根据屈雷斯加条件所得的结果相比较。
（54）用一直径为φ10 mm的黄铜试样进行拉伸试验，记录下的最大载荷为27.5kN，出现缩颈时的断面收缩率φ=20%，试求其真实应力—应变曲线方程并绘出相应的曲线。
（55）已知材料的应力—应变曲线方程为S=B∈0.4，直杆已有相对伸长ε=0.25，试问：相对伸长再增加多少材料才能发生缩颈？
（56）塑性变形时应力应变关系有何特点？为什么说塑性变形时应力和应变之间的关系与加载历史有关？
（57）试说明增量理论与全量理论的关系和各自的使用范围？
（注：以下59-63题均假设材料服从米塞斯屈服准则）
（58）有一薄壁管材料的屈服应力为σs，承受拉力和扭矩的联合作用而屈服。现已知轴向正应力分量σz=σs/2，试求剪应力τzθ以及应变增量各分量之间的比值。
（59）设处于塑性状态的5个质点，其主应力状态分别为：①（2σ，σ，0）；②（σ，0，-σ）；③（0，-σ，-2σ）；④（σ，0，0）；⑤（0，-σ，-σ）。现设在某一极短时间内产生很小的变形，且各点都是ε1=2×10-3，试求其余的主应变分量。
（60）已知塑性状态下某质点的应力张量为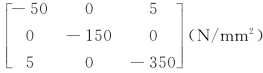
，应变分量dεx=0.1δ（δ为一无限小量，下同）。试求应变增量的其余分量。
（61）某理想塑性材料，屈服应力为150N/mm2，已知某点的应变增量为dεij=
，平均应力为σm=50N/mm2，试求该点的应力状态。
（62）有一刚塑性硬化材料，其硬化曲线、即等效应力—应变曲线为
mm2。某质点承受两向应力，应力主轴始终不变。试按下列两种加载路线分别求出最终的塑性全量主应变ε1，ε2，ε3：
①主应力从0开始直接按比例加载到最终主应力状态为（300，0，-200）N/mm2；
②主应力从0开始按比例加载到（-150，0，100）N/mm2，然后按比例变载到（300，0，-200）N/mm2。
（注意：如把加载路线在σ1-σ2坐标平面上画出，即可发现第二种加载路线中含有卸载过程。）
（63）已知二端封闭的长薄壁管容器，半径为r、壁厚为t，由内压力p引起塑性变形，若轴向、切向、径向塑性应变增量分别为
，如果忽略弹性应变，试求各塑性应变增量之间的比值（即
）。（提示：先求出应力偏量）
（64）主应力法求解塑性加工问题的原理是什么，为什么说这是一种近似计算方法？
（65）一20号钢圆柱毛坯，原始尺寸为50mm×50mm，在室温下压缩至高度h=25mm，设接触表面摩擦切应力τ=0.2S。已知S=746∈0.20MPa，试求所需的变形力P和单位流动压力p。
（66）在平砧上镦粗长矩形截面的钢坯，宽度为a、高度为h、长度l>>a，若接触面上摩擦条件符合库伦摩擦定律，试用主应力法推导单位流动压力p的表达式。
（67）镦粗一圆柱体，侧面作用有均布压应力σ0，如题图4所示。设摩擦切应力满足常摩擦条件，试用主应力法求解单位流动压力p。
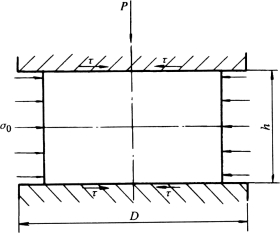
题图4 圆柱体镦粗
（68）试求圆锥凹模拉拔圆棒时的单位拉拔力（采用球形坐标，如题图5所示）。设材料为理想刚塑性材料，近似塑性条件为σr+p=S（p>0），图中A为轴向投影面积。
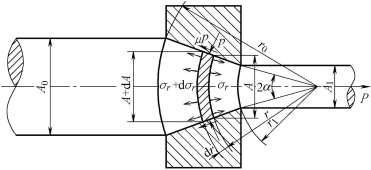
题图5 拉拔时基元体受力分析
（69）何谓速度间断线（或速度不连续），它具有哪些速度特性？
（70）何谓速端图？如何绘制速端图？
（71）上限法求解变形力有哪几种基本方法，它们的基本要点是什么？
（72）试比较板条平面应变挤压时，题图6所示的两种Johnson上限模式的上限解。
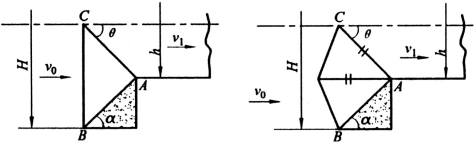
题图6 平面应变挤压时的两种Johnson上限模式（H/h=2，θ=α=π/4）
（73）试绘出题图7所示板条平面应变拉拔时的速端图，标明沿各速度不连续线的速度不连续量的位置，并计算出刚性三角形块ΔBCD的速度表达式。
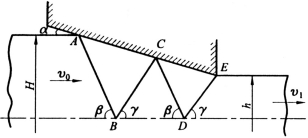
题图7 平面应变拉拔的Johnson上限模式
（74）试按题图8所示的板条不对称平面应变挤压的Johnson上限模式，绘制速端图，并确定流出速度的大小及方向（γ角）。
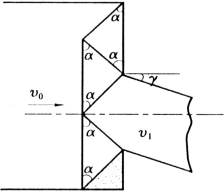
题图8 不对称平面应变挤压的Johnson上限模式（α=π/4）
（75）题图9为平锤头平面应变局部压缩薄板坯的示意图，设接触摩擦应力τf=mK，试用Avitzur上限模式求其不计侧鼓时的单位流动压力p（或nσ）的表达式。
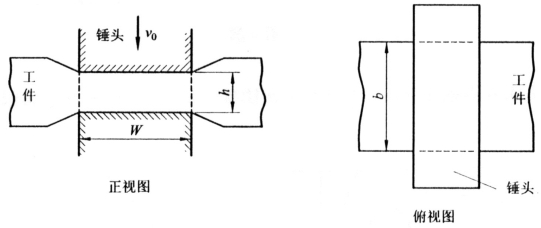
题图9 平锤头平面应变局部压缩薄板坯示意图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
