马氏体相变的G-T模型优化：探讨马氏体相变的G-T模型

马氏体相变的G-T模型也是一个具有代表性的模型。A.B.Greninger，A.R.Troiano于1949年测得Fe-22Ni-0.8C合金的单相奥氏体转变为马氏体时惯习面为{259}γ，垂直于惯习面的平面的倾动值，即倾动角φ=10°45'，位向关系与K-S关系稍有偏差：

据此G-T关系，他们以均匀切变和非均匀切变的合成方式，来满足Fe-Ni-C合金马氏体相变的晶格重构、外形改变、惯习面等方面的要求，设计了G-T模型。

G-T模型指出，假定有一个沿着惯习面的切变满足倾动角的要求而不能满足晶体结构的要求时，可以在主切变的基础上沿着“马氏体”晶面进行第二次切变，以便满足两方面的要求。沿着惯习面的第一次切变为主切变，是均匀切变，而第二次切变是非均匀切变。均匀切变和非均匀切变的示意图见图15-17。

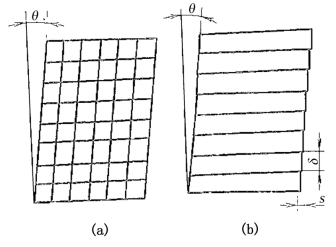
图15-17　晶面切变示意图

（a）均匀切变；（b）非均匀切变

从图15-17可见，为了获得宏观切变角θ，可以采用均匀切变，也可以采用非均匀切变。非均匀切变可以通过δ和s的调整，采用的方式有滑移和孪生两种。但δ值要比晶格常数大得多，非均匀切变不改变晶格类型及参数。

图15-18是G-T模型的示意图，其中图15-18（a）表示以惯习面（中脊面）为基准的均匀切变，即主切变。图15-18（b）表示二次切变（滑移）的发生面，以及切变后外形的变化。二次切变时在经过主切变的“马氏体”中沿着{211}α晶面，在方向反复地进行滑移。(www.xing528.com)

图15-18　G-T模型

G-T模型认为，当非均匀切变区间距δ小于一定数值时，配以适当的切变量s，二次切变不仅能调整马氏体的外形，发生宏观为θ的切变，而且，还可以对晶格和位向起调整作用，使其基本上能符合新相的要求。如果从图15-19的K方向看去，二次切变的情形如图15-19所示。其中θ为12～13°，δ有十几个原子层厚。

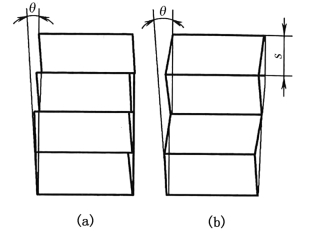
图15-19　二次切变示意图

（a）滑移；（b）孪生

G-T模型完成两种切变后，并没有完全达到实际马氏体晶格参数的要求，为此，仍需要调整晶格参数。

G-T模型的缺点仍然是与实际不完全符合，如该合金的惯习面实际是{225}γ，而非{259}γ。与ωc1.4%的钢中马氏体的惯习面也不相符。虽然预示着马氏体中存在位错和孪晶，但是不能解释马氏体中复杂的缠结位错形态和层错亚结构的成因，而且在许多马氏体中没有孪晶。两次切变消耗的切变能太大，计算共需切变能248×103J/mol，，这是相变驱动力所不能达到的。