应用上限法优化上限

1.Johnson上限模式及应用

Johnson上限模式是W.Johnson于20世纪50年代末用来研究平面应变问题所采用的上限法求解方法。它的基本思路是设想塑性变形区由若干个刚性三角形构成，塑性变形时完全依靠三角形场间的相对滑动产生，变形过程中每一个刚性块是一个均匀速度场，块内不发生塑性变形，于是块内的应变速度=0。因此，式（11-68）的能量基本方程中，若不计附加外力及其他功率消耗的话，其塑性变形功率消耗部分也为零，则上限功率表达式变为

Johnson上限模式求解的基本步骤为

（1）根据变形的具体情况，或参照该问题的滑移线场，确定变形区的几何位置与形状，再根据金属流动的大体趋势，将变形区划分为若干个刚性三角形块。

（2）根据变形区划分刚性三角形块情况，以及速度边界条件，绘制速端图。

（3）根据所作几何图形，计算各刚性三角形边长及速端图各刚性块之间的速度间断量，然后按式（11-69a）计算其剪切功率消耗。

（4）求问题的最佳上限解，一般划分刚性三角形块时，几何形状上包含若干个待定几何参数，所以须先对待定参数求极值确定其具体数值，进而求得最佳的上限解。

这里应指出的一点是，刚性三角形块划分时，要注意当任一刚性三角形的任意两边同时邻接同速度边界条件，则该三角形的速度即为该边界速度。

例题11-1 平冲头压入半无限体。

根据该问题的变形特点，设想其上限模式如图11-26所示，由于对称性，只研究其右半部分。变形区由三个刚性等腰三角形块构成，设其底角为α（待定参数），并设接触表面光滑无摩擦。三角形各边，除两侧自由表面外，都是速度间断面。图中虚线表示金属质点的流线。设冲头压下速度为=1。据此，可绘出其速端图，如图11-26（b）所示。作速端图时需要注意：进入速度不连续线的合速度矢量，加上不连续线上的剪切矢量，等于速度不连续线出去的合速度矢量。

因此，各块间的剪切功率计算式为

式中，p*为平均单位压力的上限解。

图11-26　平冲头压入半无限体的速端图

根据图11-26的图形的几何关系，各速度间断线的长度为

式中，W为冲头宽度。

同样，根据速端图可计算出各速度间断面上的速度不连续量分别为

将它们代入上式，经整理后得

于是

其应力状态系数（上限法中常称之为功率消耗系数）为

对待定参数tanα进行优化，即取极值dp/d（tanα）=0，得，即α=54°44'，将其代回原式，得这一问题在上限模式下的最佳上限解为，而这一问题的精确解（滑移线场解）为nσ=2.57，上限解高了约10%。如选用更接近滑移线场的上限模式，则精度可以提高。

2.Avitzur上限模式及应用

Avitzur采用的上限模式为连续速度场模式，其基本思路是把整个变形区内金属质点的流动用一个连续速度场=fi（x，y，z）来描述，同时要考虑塑性区与刚性区界面上速度的间断性及摩擦功率的影响。因此，Avitzur上限模式的基本能量方程与式（11-68）是一致的，常简化为

令p*为工具与工件接触面上的单位流动压力的上限解，为工具的法向速度，A为接触面积，根据上限原理，有

式中，Nd为塑性变形功率消耗，即

ND为速度间断面上剪切功率消耗，即

Nf为接触面上摩擦功率消耗，即

Nq为附加外力消耗的功率（取“+”号）或向系统输入的附加功率（取“-”号），即

但应注意，以上各式右边中的速度场以及σij等都是运动学许可的。

下面讨论塑性变形功耗的计算。

将单位体积塑性功表达为

写成速率形式，并对体积积分。对于刚塑性材料，应变即为塑性应变，略去上标“p”，可得(www.xing528.com)

根据圣维南流动方程，则

Mises屈服准则可以写为

将式（11-74b）、（11-74c）代入式（11-74a）得

式中，，为等效应变速率。若取，则有

例题11-2 直角坐标平面应变问题——考虑侧鼓时板坯的平锤压缩

平锤压缩板坯时，由于接触表面的摩擦阻碍作用，使表面层材料的水平流动速度小于中心层的水平流动速度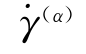，因而会出现侧面鼓形，如图11-27所示。若z轴方向（垂直纸面）的长度远远大于高度h和宽度W，则z轴方向的应变极小，可简化为平面应变问题。平面应变适合于用直角坐标描述，其坐标原点取在板坯的几何中心点O上，由于变形的对称性，可以仅研究右上部分。

图11-27　带侧鼓时的板坯平锤压缩

为了建立考虑侧面鼓形时的运动学许可速度场，首先分析不考虑侧鼓时的运动学许可速度场。由边界条件设和y=±h，，设与坐标成线性关系，即

按体积不变条件，平面应变问题有，于是，积分得

由边界条件x=0，=0得f（y）=0，于是得

可见，不考虑侧鼓时，与y无关，即从中心至表层是均匀的。当考虑侧鼓时，沿y的分布不均匀，即=f（x，y）。现根据vx逐渐减小的特点，假设沿坐标y轴是按指数规律变化的，可令

以此作为设计考虑侧鼓时的平锤压缩板坯的运动学许可速度场的出发点，来研究整个运动学许可速度场的情况。

根据平面应变的几何方程和体积不变条件得

由式（11-75b）第二式得

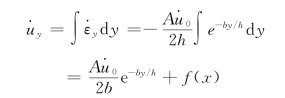
由 边界条件，求得，因此

在y=h的表面上，，所以，求得待定参数为

于是

这样，该式便只剩下一个待定参数b了。

将式（11-75c）代入式（11-75b），得

将式（11-75d）代入式（11-71），积分经整理后得

设接触表面上摩擦应力τf=mK，m为摩擦因子，m=0～1.0。接触表面上的速度不连续量，代入式（11-73），得

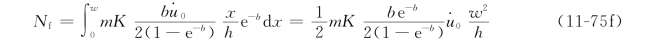
于是

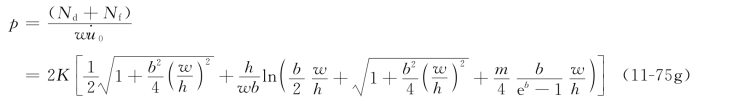
对上式求极值可确定待定参数b，即，经一系列数学推导后求出：

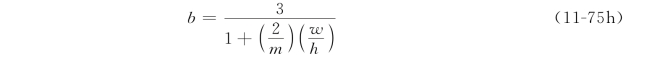
将b值代入式（11-75g），得该模式下的最佳上限解为

若不计侧面鼓形，上式右边第三项为零。