虚功原理与基本能量方程

虚功原理也称虚位移原理，它是力学中应用范围很广的原理之一。它表达了质点系平衡的普遍规律，可以用来研究质点系、刚体和弹、塑性体的平衡问题。虚功原理可叙述如下：

外力作用下变形体处于平衡状态，若在任何方向给该物体一个微小虚位移（可能位移），则这时外力在虚位移上所作的虚功必等于物体内应力在虚变形上所作的虚功（虚应变能）。

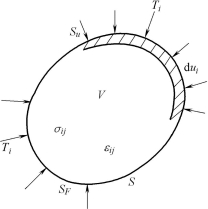
图11-21　变形体上的外力、内力、位移、应变

现假设变形体的体积为V（见图11-21），表面积为S，作用的外力为Ti，当给以微小的位移增量dui时，物体中相应的应力场σij引起应变增量为dεij，则虚功原理可表达成下式：

上式左边部分表示物体上外力所作的虚功（增量），右边部分表示物体内应力所作虚功（虚应变能增量）。式（11-57）称为虚功方程或基本能量方程。

在讨论上述虚功方程时，假设变形体内速度分布是连续的。但在实际塑性问题中，变形体为刚性区和塑性区的组合体，存在速度间断，应用虚功方程时必须加以考虑。

滑移线场理论中的刚塑性边界就是速度出现间断的例子。设物体由速度间断面SD分为Ⅰ和Ⅱ两个区域，在微元面积dSD上的速度间断情况如图11-22所示。由于塑性变形中物体保持体积不变，材料在法线方向不分离也不重叠，因而Ⅰ、Ⅱ区的法向速度必然相等，即。切向速度可以发生间断，速度间断值（跳跃量）为，这样就造成了Ⅰ、Ⅱ区的相对滑移。

所谓速度间断面，实际上是沿SD面的一个速度急剧而连续变化的薄层区域，薄层厚度Δt趋近于零，如图11-23所示。变形体由于存在速度间断而多消耗的功率为(www.xing528.com)

式中，τ为沿dSD切线方向的剪应力。在塑性变形时，τ=K。对于存在多个速度间断面的情况，其所消耗的总变形功率为

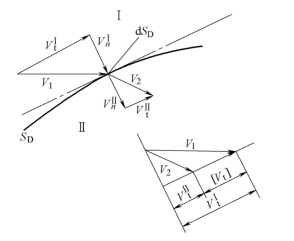
图11-22　速度间断面上的速度间断

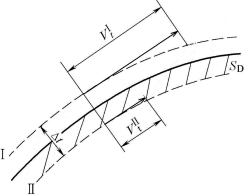
图11-23　速度间断薄层区

于是，变形体存在速度间断时的虚功（率），方程应写成以下形式：