镦粗零件的主应力法分析

1.镦粗变形的特点

在外力作用下，使坯料高度减小，横截面增大的塑性成形工序称为镦粗。镦粗通常是在两个平行的平砧之间对坯料进行压缩。镦粗坯料的形状、尺寸及与砧板之间的接触状态对镦粗变形有很大影响，不同的截面和尺寸、不同的摩擦状态，镦粗时的应力应变状态存在很大的差异。

坯料在无摩擦的平行砧板间进行镦粗，变形前的直棱和平面变形后仍然是直棱和平面，而且俯视图上的外形保持相似，这样的变形称为均匀镦粗。不难理解，此时，金属质点沿水平方向的流动必为由横截面中心向四周呈放射状流动。

金属塑性成形时质点的流动规律遵循最小阻力定律，即在塑性成形中，当金属质点有向几个方向移动的可能时，它会向阻力最小的方向移动。但是，在实际镦粗中.接触面上不可避免地存在摩擦，这就导致了镦粗时的不均匀变形。下面以圆柱体镦粗为例来分析镦粗变形的特点。

当圆柱体的高径比时，镦粗后呈现鼓形，即两端直径小，中间直径大（见图11-9）。利用网格法可以得到镦粗时坯料子午面上的网格变化。从中可以看出坯料内部的变形是不均匀的，为了便于分析，将变形区按变形程度大致分为3个区，如图11-10所示。

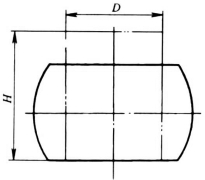
图11-9　平砧镦粗示意图

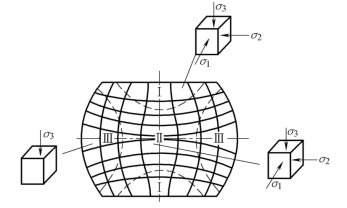
图11-10　坯料子午面网格变化及各区域应力情况

区域Ⅰ是和工具的上下砧面接触的区域，变形程度最小，称为难变形区。区域Ⅱ处于上下两个难变形区域Ⅰ之间，变形程度最大，称为大变形区。区域Ⅲ是外侧的鼓形区部分，变形程度居中，称为小变形区。变形不均匀产生的主要原因是工具与坯料端面之间存在摩擦。

由于表层受到的摩擦阻力很大，区域Ⅰ内的金属质点受三向压应力。越靠近接触面中心部分.金属流动受到外层阻碍和摩擦阻力所引起的三向压应力数值也越大，变形也就越困难。因为摩擦力的影响是随离接触表面的距离而减弱的，所以区域Ⅱ受到的摩擦影响小，在水平方向上受到的压应力也较小。金属质点在轴向压应力的作用下产生很大的压应变，径向有较大扩展，同时难变形区Ⅰ对该部分有压挤作用，这些变形的综合作用导致了鼓形的形成。

在平砧间热镦粗坯料时，除摩擦力影响外，温度不均也是不均匀变形产生的原因之一。Ⅰ区金属由于与工具接触，温度降低快，变形抗力大，因此变形也较其他区域困难。

区域Ⅲ外侧为自由表面，受端面摩擦影响小，应力状态近似于单向压缩（σ3）。但是，由于Ⅱ区变形较大，金属向外流动时对Ⅲ区有径向压应力（σ2），使该区金属切向受拉应力（σ1），愈靠近坯料外表面切向拉应力越大。当切向拉应力超出材料的强度极限或切向变形超过材料允许的变形程度时，便会引起纵向裂纹。

当圆柱体的高径比时，镦粗后坯料上部和下部变形大，中间变形小，形成双鼓形（见图11-11）。这是因为与平砧接触的上下端金属受摩擦力影响形成了锥形的难变形区，外力通过它作用于与之相邻的部分，导致了双鼓形的形成。随着镦粗继续，高径比接近1时，双鼓形逐渐变成单鼓形。如果坯料更高，镦粗时容易失稳而弯曲。

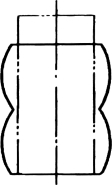
图11-11　较高坯料镦粗时形成双鼓形

当圆柱体的高径比时，镦粗的不均匀程度有所改善。

这是由于相对高度较小，上下难变形区已部分重叠（见图11-12），坯料不存在大变形区，因此鼓形程度较小。

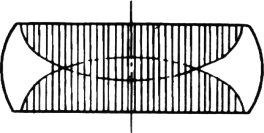
图11-12　较低坯料镦粗时的难变形区

坯料镦粗变形的不均匀性在其端面也有反映。一般情况下，镦粗毛坯的端面分为边部和心部两个不同区域。在边部区域，金属质点与工具表面有径向滑动，为滑动区；在心部区域，不存在相对滑动，称黏着区，即上下两难变形区的底面。滑动区与黏着区的相对大小与摩擦系数μ和高径比有关，μ和越大，黏着区越大。在一般坯料镦粗初期，端面尺寸的增大主要是靠侧表面的金属翻上去实现的。

2.圆柱体镦粗变形力的计算

当我们在计算中用主应力法求解圆柱体镦粗时的应力分布状态时，可以按以下步骤进行：

（1）设圆柱体毛坯的直径和高度分别为d和h，采用坐标原点在圆柱中心而z轴与圆柱轴线重合的圆柱坐标系（r，θ，z），将问题简化为轴对称问题。

（2）沿整个坯料高度方向在半径r处截取一厚度为dr、圆心角为dθ的扇形基元体，如图11-13中阴影所示。沿基元体的高度方向作用着均布的径向压应力σr和σr+dσr及切向压应力σθ。由于轴对称问题，故τrθ=τzθ=0，所以σz和σr为主应力。

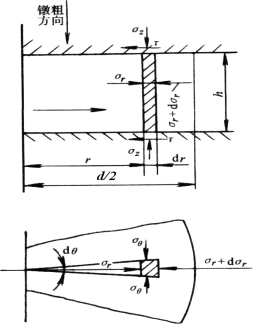
图11-13　圆柱体镦粗时基元体的应力分析

（3）列基元体径向的力平衡方程（沿r向）。

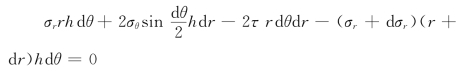
因dθ是一微小量，故sin，整理并略去高次项，得

圆柱体镦粗时，σθ=σr，代入上式得

（4）补充塑性条件。轴对称状态时，Mises与Tresca屈服准则一致，忽略摩擦切应力对屈服准则的影响，即为

所以有dσz=dσr，代入式（11-15）得

（5）引入摩擦条件。

①若采用常摩擦条件τ=μ'S，代入式（11-15）得

当r=d/2时，σr=0，由屈服准则，σz=S，得积分常数为

于是得接触面正应力为

已知接触表面正应力分布后，便可求得镦粗变形力和单位流动压力。镦粗变形力P为

单位流动压力p为

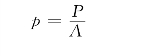
式中，A为坯料的承压面积。

圆柱体镦粗时的单位流动压力（变形力）为(www.xing528.com)

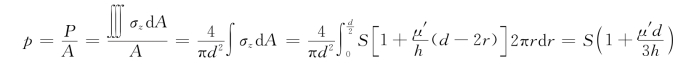
式中，承压面积。

②若采用库伦摩擦条件τ=μσz，代入式（11-15）得

对上式积分得

与常摩擦条件的边界条件一样，当r=d/2时，σr=0，σz=S，得积分常数为

于是接触面上正应力分布与摩擦切应力分别为

单位流动压力为

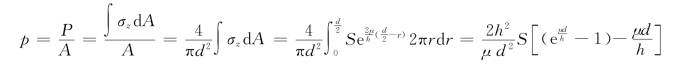
3.平面应变镦粗变形力的计算

图11-14表示平行砧板间长矩形截面毛坯的镦粗。设毛坯的宽度为b，高度为h，长度为l，假设l≫b、h，所以可按平面变形进行求解。由于对称，取右半边进行分析。设τ=μ'S（若改变摩擦条件，则推导结果不同，但推导方法和步骤不变）。

图11-14　平行砧板间平面应变镦粗及正应力σy的分布

对图中的基元板块，沿x方向列出力的平衡方程为

整理得

平面变形时的塑性条件（按Mises条件）为

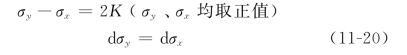
将式（11-20）代入式（11-19），得

积分，并将τ=μ'S代入，得

利用边界条件确定积分常数C，当时，则

最后得

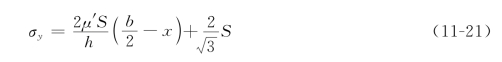
σy的分布如图11-15（b）所示。

平面应变镦粗的单位流动压力为

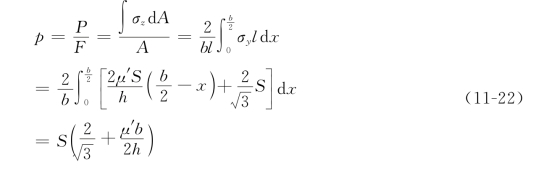
式中，承压面积。

4.镦粗时的变形功

塑性成形设备主要是根据材料成形时所需要的变形力或变形能量进行选用的。镦粗时常用的设备主要是液压机或锻锤等，其中液压机的作用力是静压力，锻锤的作用力则是冲击力。冲击力是根据能量确定的，所以锻锤类设备的选取以坯料镦粗时的变形功为基础。

假设圆柱体在镦粗过程中某瞬间的单位流动压力为p，接触面工作面积为A，变形体高度压下量为dh，则该瞬时的变形功为

设毛坯在变形瞬时高度为h，圆柱体体积为V，则。当圆柱体由初始高度h0镦粗至变形结束时高度h1，所需要的总变形功为

由前述变形力的计算可知，单位流动压力p=f（h），因此式（11-23）积分比较困难。为简化计算，以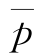表示坯料由h0至h1的单位流动压力的平均值，代入上式得

当变形量不大时，相对压缩量，式（11-24）又可写成

式中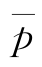，为平均单位流动压力，可根据中值定理求取或近似用

计算；p0为镦粗毛坯高度为h0时的单位流动压力；p1为镦粗毛坯高度为h1时的单位流动压力。

在热镦粗时，假设材料为理想塑性材料，材料无加工硬化，这时S为常数。假设接触表面间无摩擦，此时单位流动压力p=S，代入式（11-23）得

除用上述方法近似计算镦粗变形功外，也可将单位流动压力公式直接代入后积分求解。