塑性成形问题的基本方程和边界条件解析

金属塑性成形是利用金属的塑性，通过模具（或工具）使简单形状的毛坯成形为所需工件的技术。塑性成形工件中的位移、应变和应力的分布，决定了成形件的精度、质量和成形载荷。针对塑性成形工艺问题建立其力学模型，通过求解获得工件的塑性变形规律，位移、应变和应力的分布规律，对于工艺设计和模具设计具有重要的意义。

塑性成形过程的基本规律可以用一组微分方程来描述。例如，前面几章介绍的应力平衡方程、几何方程、屈服准则和本构方程，等等。在这些方程在所讨论的问题中常常称为场方程或控制方程。为了分析一个具体的材料成形问题，除了要给出具有普遍意义的场方程以外，还要给出由该问题的特点所决定的定解条件，在静力学问题中为边界条件，也称为边值条件。这样就把材料成形问题抽象为一个微分方程（组）的边值问题。

在微分方程求解时，要求方程数与待求的场变量数相等。有时只需求解成形工序所需的变形力，所谓变形力是指在塑性加工过程中，工具对坯料所施加的使之发生塑性变形的作用力。它是正确设计模具、选择设备和制定工艺规程的重要参数。由于塑性变形时，变形力是通过工具表面或毛坯的弹性变形区传递给变形金属的，所以为求变形力，需要确定变形体与工具的接触表面或变形区分界面上的应力分布。这可以通过将平衡微分方程和塑性条件（屈服准则）进行联解实现。但是，仅仅将平衡微分方程和塑性条件进行联解往往方程数少于待求的场变量数，这时就必须补充其他方程，如应变连续方程和本构方程，如表11-1所示。联立求解的方程数越多，求解越困难；但能求解出的场变量越多，对成形过程的描述越细致。

表11-1　平衡微分方程和塑性条件进行联解可能性分析

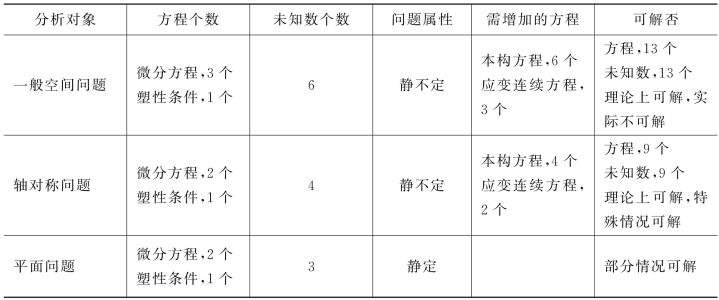
从表11-1可以看出，对于空间问题，平衡微分方程和塑性条件共有4个方程和6个未知数（σx，σy，σz，τxy，τyz，τzx），需要联解本构方程和应变连续方程，这样共有13个未知数和13个方程，理论上可以求解，但实际上是无法求解的。对轴对称问题，有3个方程和4个未知数，同样需要联解本构方程和应变连续方程，这样共有9个未知数和9个方程，理论上可以求解，但研究发现只有个别情况才能求解。对于平面问题，有3个方程和3个未知数，属静定问题，但这类问题也只有在部分情况下，才有精确解。

将塑性成形过程力学模型中的边界S分为ST、Su和Sc几部分，相应的边界条件分别表示如下：(www.xing528.com)

①ST为给定了边界面力矢量Ti的边界，在此部分边界上要满足应力边界条件：

②Su为给定了位移（或速度）的边界，在此部分边界上要满足位移（或速度）边界条件：

③Sc为两个物体之间的接触边界，在此部分边界上法向位移（或速度）必须连续，以满足材料连续性条件，但切向可以有相对运动；同时切向应力与法向应力之间应满足摩擦条件，这是一种混合边界条件。

塑性成形工艺设计和模具设计的主要任务是通过改变工件变形的边界条件来改变成形载荷和成形件的质量，所以对于边界条件的控制是十分重要的。