晶体塑性的本构方程

大多数工业用金属材料都是多晶体材料，常温下金属晶体塑性变形的机制主要是位错滑移。滑移是沿特定的晶面（原子密排面）和晶向（原子密排方向）进行的，这是这类材料塑性变形在几何学和运动学上的主要特点。由于在晶体内部存在着大量的位错，宏观上可以从体积平均的角度将滑移引起的位移和应变看成是均匀的、连续分布的，采用连续介质力学的方法进行处理。在后继屈服轨迹、塑性各向异性和变形诱导织构演化等方面的研究中，晶体塑性理论有其独特的优越性。我们首先介绍连续滑移模型所导出的单晶体塑性理论，然后简单介绍多晶体的处理方法。

1.有限应变的其他描述方法

为了便于下面的公式推导，首先引入几个分析有限变形问题常用的概念。

1）变形梯度

我们把物体中所有质点瞬时位置的集合——某一瞬时物体在空间占据的区域V称为该物体的构形。我们采用拉格朗日描述，即选择初始（即t=t0=0）时刻的构形V0作为参考构形，以便定义物体的运动和变形。如图10-36所示，采用笛卡儿直角坐标系作为参考坐标系，将构形V0中任一个质点a的坐标记为Xi（i=1，2，3）。此后某一时刻t，物体运动到一个新位置，各质点之间的相互位置关系发生了变化，物体产生了变形，质点a的位置坐标从Xi改变为xi（i=1，2，3）。显然，xi是Xi和时间t的函数，即

变形后的现时构形记为V。

图10-36　物体的构形

假设物体及其运动和变形都是连续的，则V0中每一个质点Xi仅与V中一个质点xi对应，反之亦然。因此，函数xi（X1，X2，X3，t）是单值、连续和可微的，且雅可比行列式不等于零，即

也有

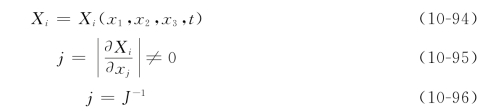
由于x是X的单值、连续和可微的函数，故有

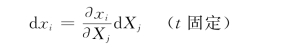
式中，称为变形梯度，它是一个二阶张量。将上式写成张量的形式为

式中，黑体字表示一阶和二阶张量，“·”表示点积运算。上式表明：变形梯度F将初始构形中任一线元dX变换成现时构形中的对应线元dx，它同时描述了运动与变形过程中线元长度和方向的变化。可以F分解成一个纯变形加上一个刚体转动的组合，称为极分解；另一方面，也可以将F分解成一个纯塑性变形加上一个弹性变形与刚体转动的组合，称为乘法分解。

2）速度梯度及其分解

如图10-37所示，在某一瞬时的现时构形中，任一质点P具有速度v，在P的邻域内的另一点Q具有速度v+dv。在同一时刻，由于坐标不同而产生的速度变化是：

式中称为速度梯度，记为Lij，它也是一个二阶张量。如果说变形梯度F表明一段时间中变形与转动的大小，则速度梯度L表明某一段时刻变形与转动的快慢。

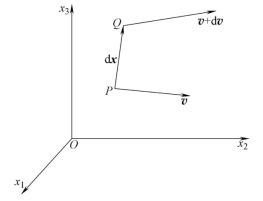
图10-37　质点速度在空间中的变化

可以将L分解为一个对称张量d和一个反对称张量ω之和：

式中，d即为应变速率；ω为旋转速率。

2.晶体塑性变形几何学

在分析单晶体的塑性变形时，如图10-38所示，可以对变形梯度进行如下乘法分解：

其中，Fe代表弹性变形（即晶格畸变）和刚体转动所产生的变形梯度；Fp则表示晶体沿着滑移方向的均匀剪切所对应的变形梯度。式（10-99）所代表的变形过程可看作是分两阶段完成的：首先是没有畸变的晶格中由位错滑移产生变形的梯度Fp，然后晶格在发生弹性畸变的同时伴随着刚体转动，从而产生变形梯度Fe。

设变形前晶体中第α个滑移系中沿滑移面法向和滑移方向的单位向量分别为，由于变形晶格发生畸变和刚体转动后，遵循矢量的变换关系它们分别为

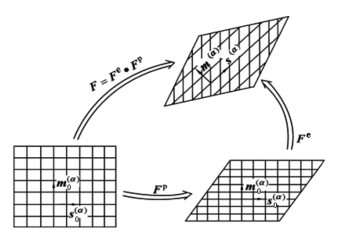
图10-38　变形梯度的分解

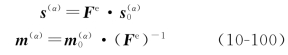
s（α）和m（α）不再是单位向量，而是仍保持正交；其正交性可以由上述矢量的点积直接验证。

速度梯度L可由变形梯度F计算如下：

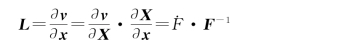
其中，X表示初始坐标，x表示现时坐标。与变形梯度的乘法分解相对应，速度梯度也可分解为分别与滑移和晶格畸变加刚体转动相对应的两部分：

下面分析怎样将各滑移系中由滑移引起的剪切应变与整体的塑性变形联系起来。首先考虑无弹性畸变的中间构形中的一个滑移系α中由滑移剪切应变dγ（α）引起的位移增量，如图10-39所示。其中均为单位向量，P为晶体中任意一点，其矢径为x，由剪切引起的该点位移为

图10-39　滑移引起的位移增量

将上式写成速率形式并对所有滑移系求和得

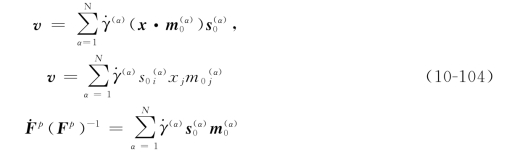
其中表示第α个滑移系的滑移剪切率，对所有开动的滑移系求和。

考虑到式（10-100），有

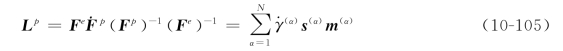
将速度梯度分解为变形速率张量和旋转速率张量之和，而后者又可以分别分解为位错滑移产生的部分和弹性畸变及刚体转动产生的部分，即

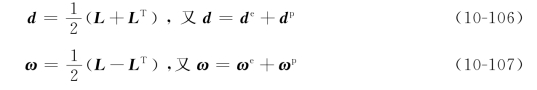
上式中两张量的弹性部分为：(www.xing528.com)

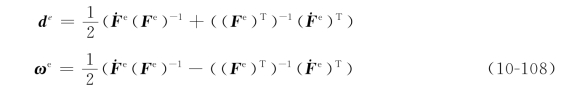
其中，de引起晶格的畸变；ωe引起晶格的转动，是变形诱导织构产生的原因。

塑性部分可由式（10-105）得到

其中

这里，ωp虽然引起单晶体整体的转动，但并不引起晶格方位的变化，如图10-38所示。

3.单晶体的本构关系

如前所述，金属的变形可以分解为弹性变形部分和塑性变形部分，其中弹性变形与应力的关系总是遵循虎克定律。为了将虎克定律推广到大变形问题以及书写的方便，我们对虎克定律进行了改写。虎克定律式（10-60）是将应变表示为应力的线性函数；如果将它看作关于应力的线性方程组，则可以将应力表达成应变的线性函数：

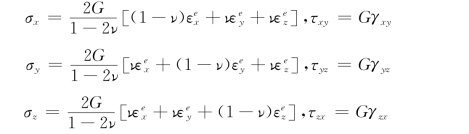
利用求和约定写成张量形式为

其速率形式为

其中，符号“∶”称为双点积，按照求和约定，它表示对方程右端的两个下标都要求和。这种形式用于已知应变速率求应力的场合，通常在有限元计算中就是如此。

在大变形过程中，物体中的质点在变形过程中不可避免地要伴随刚体转动，如果我们在每一质点处建立一个由该点的物质纤维组成的局部坐标系，则每一瞬时局部坐标系与固定不动的参考坐标系的对应关系都在变化，因此应力、应变等都应该采用速率或增量形式表示。由于刚体转动不应引起新的弹性变形和应力增量，因此需要定义能排除刚体转动的影响的应力变化率，使得在质点保持应力状态不变（如单向拉伸）而仅发生刚体转动时，应力变化率为零。满足上述要求的应力变化率有多种，常用的是柯西应力（即定义于现时构形的应力）的久曼速率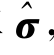，在固定参考系中表达为

其中是固定参考系中的应力变化率，ω是局部物质坐标系相对于固定参考系的转动速率。类似地，在与晶格一起旋转的直角坐标系中的柯西应力张量的变化率为

其中，ωe是晶格坐标系相对于固定参考系的转动速率。

由于滑移不影响晶体的弹性性质，在固定参考系中单晶体的弹性本构方程即可写成

其中，Cc为晶体的正交各向异性弹性张量，为简化计，以下取为各向同性弹性张量Ce。

式（10-113）减去式（10-112），并将式（10-108）、式（10-110）、式（10-111）代入，可得单晶体的本构方程为

其中

4.剪切应变速率的计算

由单晶体本构方程式（10-115）计算应力速率时，需要先求出各滑移系中的剪切应变速率。它是根据硬化方程来计算的。硬化方程有与速率相关（即黏塑性）和与速率无关（即塑性）两种形式。应用较为方便的是速率相关的硬化方程，常采用如下形式的幂函数：

其中，g（α）称为参考剪切应力称为参考剪切应变速率。若在整个变形过程中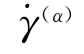=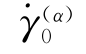，则τ（α）=g（α）就成为在剪切应变速率为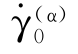时的τ（α）-γ（α）关系曲线的方程。m为应变速率敏感指数。当m=0时，即为与应变速率无关的情况。但是要注意，当m→0时，计算不稳定。上式中的sign（τ（α））表示τ（a）的符号，其作用是使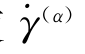与τ（a）的方向一致。

设γ（α）=0时，g（α）的初值为τ0，τ0即是各个滑移系中位错开始滑移时的阻力。虽然按式（10-116）计算时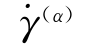一般不会为零，即各个滑移系总是开动的，但是，当τ（a）<g（α）时，其值迅速减小，当时，通常可以忽略不计。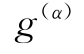的演化由下式确定：

其中，hαβ称为硬化系数，其含义是滑移系β中的滑移剪切应变对滑移系α所造成的硬化。

5.硬化系数及其演化

晶体塑性理论中，确定硬化系数hαβ是一项困难的任务。它是变形历史、变形温度和速度的函数，其分量也很多。对于高层错能材料，硬化主要是由滑移产生的，在实际分析中，对hαβ可采取简化的计算方法。例如，可取hαβ为如下形式：

式中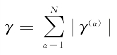，，h（γ）是累积滑移应变γ的函数，表明硬化的总趋势；合金与纯金属具有不同的硬化特点，前者具有高的初始屈服应力及低的硬化率，流动应力很快趋于饱和值，后者显示出低的屈服应力并且不趋于饱和，故h（γ）可分别取如下函数形式：

式中，h0和hs分别为初始和饱和硬化率，一般可取hs=0；τs为饱和剪切应力；n为应变硬化指数。式（10-118）中的qαβ可用下式近似计算：

其中，q为潜在硬化率与自硬化率之比，其值一般为1～1.4，可简单地取为

我们知道，位错滑移导致位错增殖，从而导致后续的滑移阻力增大，这是应变硬化的基本原因。滑移系β中的滑移所造成的硬化，在与之共面的滑移系中（包括其本身）强度相同，而在与之不共面的其他滑移系中强度更高，如式（10-121）所示；这是由于滑移系β中的位错对于其他滑移系形成了所谓的“位错林”。对非共面滑移系位错间相互作用的强度进行更仔细的区别处理，可以给出qαβ的更精确的取值。

对于低层错能材料，孪晶在塑性变形中起重要作用，其硬化规律还要考虑孪晶的影响，较为复杂。

6.多晶体塑性模型

多晶体是由大小、形状、方位各不相同的单晶晶粒集合而成的集合体。假设各相邻晶粒彼止接触，变形后不产生裂缝，则塑性力学中的平衡方程及变形协调条件均应在集合体中得到满足。

从理论上说，若已知各晶粒的本构方程，则采用离散化的方法可以得到整个多晶集合体的本构关系。例如，可将每个晶粒离散为一个或多个有限单元，在研究塑性变形的物体的局部变形情况时可以采用这种建模方法，这种模型能够用来考察各个晶粒的不同取向及晶界的约束对变形的影响。但是如果要对塑性成形中一个工件进行分析，则因为其中所包含的晶粒数目极大，不能采用以上方法。

另一类方法是建立在统计平均的基础上的。假设多晶集合体是均匀的，每一点都呈现集合体的统计平均特性。建立这一类模型关键是要对其中任一个晶粒与其周围的其他取向的晶粒之间在应力、应变等方面的关系进行适当的假设和处理。建立多晶集合体模型的方法主要有如下3种：①泰勒型模型：假定集合体中所有晶粒应变相同，都等于宏观应变，即强加了单个晶粒与周围其他晶粒之间的变形协调条件，但由于多晶体的各个晶粒方位各不相同，所以相同的应变在各个晶粒中所对应的应力状态各不相同，在晶界处不能满足应力平衡条件，具有近似性；②Sachs型模型：假定集合体中所有晶粒都处于与宏观应力相同的均匀应力场中，即强加了应力平衡条件，但对于其中各个晶粒而言，相同的应力状态产生的应变也是各不相同的，所以在晶界处不满足变形协调条件，也具有近似性；③自洽理论：它采用较为严格的力学推导，建立了单个晶粒与假定为均匀的周围介质之间的关系，能同时满足平衡条件与协调条件，但计算较为复杂，其中泰勒型模型因应用十分方便，而且与实验吻合也较好，因而应用较广泛。

对一个多晶体质点进行应力、应变分析时，首先要依次对其中的每个晶粒进行本构方程的求解，然后对各单晶体中相关物理量的数值进行体积加权平均，所得的结果就是该质点处的多晶集合体中该物理量的数值，即

式中，Ai和A分别为第i个晶粒中所求物理量的值和集合体该物理量的平均值；Vi和V分别为第i个晶粒所占体积和集合体的总体积；N为晶粒个数。

多晶体中晶粒方位在空间中分布的规律称为取向分布函数（ODF）。一般采用单个的晶格局部坐标系与物体的整体坐标系之间3个欧拉角的分布规律来表示。实际多晶材料的取向分布函数可以利用X射线衍射并进行分析计算获得。它是建立精确的多晶体模型的基础。