塑性本构方程的探究与应用

1.塑性本构方程的特点

前述弹性变形时的应力—应变关系有如下特点：①应力与应变成线性关系；②应力主轴与应变主轴重合；③由于弹性变形是可逆的，所以应力与应变之间是单值关系，如6个应力分量已知，即可由广义虎克定律求出6个应变分量，反过来也一样，也就是说一种应力状态总是对应一种应变状态，而与加载路径无关；④应力球张量使物体产生弹性的体积变化，所以泊松比ν<0.5，参见式（10-62）。

塑性变形时全量应变与应力之间的关系则完全不同：①应力与应变之间的关系是非线性的；②全量应变主轴与应力主轴不一定重合；③塑性变形是不可恢复的，应力与应变之间没有一般的单值关系，而是与加载历史或应变路径有关；④塑性变形时可以认为体积不变，即应变球张量为零，泊松比v=0.5。对于②、③两个特点，我们举一些实例加以说明。

最简单的例子就是单向拉伸（见图10-26）。在弹性范围内，应变只取决于当时的应力；反之亦然。例如，σc总是对应εc，不管σc是由σa加载而得，还是由σd卸载而得。在塑性范围内，如果是理想塑性材料（图10-26中的虚线），则同一σs可以对应任何应变；如果是硬化材料，则由σs加载到σe，对应的应变为εe。如由σf卸载到σe，则应变为ε'f，所以不是单值关系。

图10-26　单向拉伸时的应力—应变曲线

图10-27　拉剪复合应力时的塑性应力应变关系

（a）应力—变曲线；（b）屈服轨迹

表10-2　加载路线不同时的应力和应变

（续表）

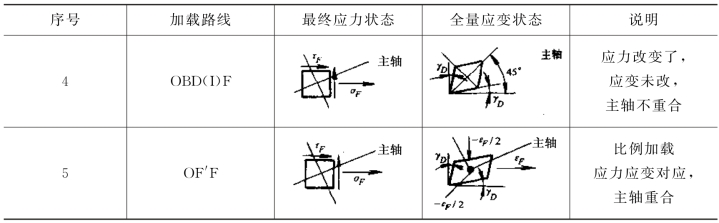
下面再举一个二向应力的例子。设一刚塑性硬化材料的单向拉伸及纯剪时的真实应力—应变曲线如图10-27（a）所示，它在σ-τ坐标平面上的屈服轨迹见图10-27（b）。现将材料单向拉伸至初始屈服点A后，再继续拉至C点，这时，应力为σc，应变为ε1=εc、ε2=ε3=-εc/2（见表14-2第一行），此时材料的后继屈服轨迹为CFD，现设减小拉应力，加上剪应力，通过后继屈服轨迹里面的任意路径，例如CEF、CJF或CF，等等，变载至F点；这时应力为σF、τF，但由于F点和C点在同一屈服轨迹上，等效应力并未增加，不能进一步变形，所以应变状态并无变化（见表14-2第二行），于是应力和应变并不对应，而且主轴不重合。如果从初始状态先加纯剪应力，通过屈服点B到达D点，这时的应力和应变见表10-2的第三行。如同样经后继屈服轨迹里面的任意路径变载至F点，则应力和应变见表10-2的第四行。如果从初始状态沿直线OF'F到达F点，则应力和应变见表10-2第五行，这时它们的主轴重合。上述的第一、三、五种加载路径称为简单加载。由表中可看出，同样的一种应力状态σF、τF，由于加载路径不同，就有好几种应变状态；同样一种应变状态，也可有几种应力状态；而且应力、应变主轴不一定重合。从上述简单的例子中，可以看到，离开加载路径来建立应力与全量塑性应变之间的普遍关系是不可能的。因此，—般情况下只能建立起应力和应变增量之间的关系，然后根据具体的加载路径，具体分析。另一方面，从上述例子中也看到，在简单加载的条件下，应力和应变的主轴重合，而且它们之间有对应关系，因此可以建立全量理论。

2.加、卸载准则和杜拉克公设

1）加载和卸载准则

（1）理想塑性材料的加载和卸载。理想塑性材料的屈服应力是不变的，所以加载条件和屈服条件一样，在应力空间中，加载曲面的形状、大小和位置都和屈服曲面一样。当应力点保持在屈服面上时，称之为加载，这时塑性变形可任意增长（后面将证明，各塑性应变分量之间的比例不能任意，需要满足一定关系）；当应力点从屈服面上变到屈服面之内时就称之为卸载。如果以f（σij）=0表示屈服面，则可以把上述加载和卸载准则用数学形式表示如下：

在应力空间中，屈服面的外法线方向n向量的分量与成正比表示应力增量向量指向屈服面内表示n·dσ=0，即应力点只能沿屈服面上变化，仍属加载（见图10-28）。由于屈服面不能扩大，dσ不能指向屈服面以外。

（2）强化材料的加载和卸载。强化材料的加载条件和屈服条件不同，它随着塑性变形的发展而不断变化。它一般可表示为下述形式：

图10-28　理想塑性材料屈服面上的应力增量

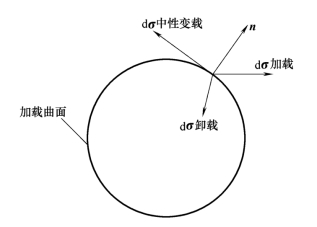
图10-29　强化材料屈服面上的应力增量

其中，Hα（α=1，2，…）是表征由于塑性变形引起的物质微观结构变化的参量，它们与塑性变形历史有关。例如，流动应力、背应力αij等。在应力空间内，式（10-70）所表示的加载曲面随Hα的变化而改变其形状、大小和位置。

以下讨论强化材料的加载和卸载准则，它和理想塑性材料的不同之处是这时dσ在指向屈服面之外时才算加载（见图10-29），而当dσ正好沿着加载面变化时，加载面不会变化，这种变化过程叫做中性变载过程，这个过程中应力状态发生变化，但不引起新的塑性变形。对单向应力状态或理想塑性材料没有这个过程。当dσ向着加载面内部变化时，则是卸载过程，用数学形式表示为

2）杜拉克（Drucker）强化公设

考察如图10-30所示的一个单向应力状态下强化材料的应力循环过程。设材料从某个应力状态σ0开始加载，在到达加载应力σ后，再增加一个dσ，它将引起一个新的塑性应变增量dεp。在这样一个变形过程中，应力做了功，如果现在将应力重新降回到σ0，弹性应变将得到恢复，弹性应变能得到释放，然而塑性应变能部分则是不可逆的，在这样一个应力循环过程中，所作的功恒大于零，也即消耗了功，这部分功转化成热能以及引起材料微观组织变化的能。这个功是消耗于塑性变形的，称为附加应力所做的塑性功，可表示如下（见图10-30中的阴影面积）：

图10-30　应力循环

若σ0正好处于塑性状态，即σ0=σ，则在dσ增加和dσ减小的应力循环中塑性功为正，这里可表示为

其中，等号仅对理想塑性材料成立。

杜拉克根据这一性质及有关热力学的规律，提出了弹塑性介质强化的假设，一般叫做杜拉克公设。杜拉克公设可表述如下：

设在外力作用下处于平衡状态的材料单元体上，施加某种附加外力，使单元体的应力增加，然后移去附加外力，使单元体的应力卸载到原来的应力状态。于是，在施加应力增量（加载）的过程中，以及在施加和卸去应力增量的循环过程中，附加外力所作的功不为负。

在一般应力状态下，式（10-72）和（10-73）分别为

下面我们说明不等式（10-74）和式（10-75）的几何意义。为此我们将应力空间σij和塑性应变空间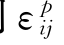的坐标重合。这时应力状态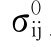用向量OA0表示，应力σij用向量OA表示，塑性应变增量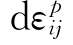用向量AB表示，应力增量用AC表示。σij-是向量A0A。这时不等式（10-74）（见图10-31）就表示为

它表示向量A0A与AB的夹角不大于直角。设在A点作一超平面垂直于AB。要保证上式成立，则位于加载曲面上或其内的所有应力点A0只能在过屈服面上任何点所作的超平面的同侧，这就是说，加载曲面必须是外凸的。这里外凸包括加载面是平的情形。

其次，讨论代表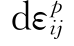的向量AB的方向问题。假定A点处在光滑的加载面上，在这点处的外法线向量n存在而且是唯一的。我们将证明AB的方向与n的方向一致。实际上如果向量AB不与n的方向重合，则我们总可以找到一点A0（在加载面上和加载面内）使AB与A0A的夹角超过直角。只有AB和n重合，AB与A0A的夹角才不会超过直角。这时，的方向就可以用数学形式表示为

其中，dλ>0为一比例系数。上式表明，塑性应变增量各分量之间的比例可由σij在屈服面f（σij）上的位置决定，而与dσij无关。上式称为塑性流动法则。

图10-31　式（10-74）和式（10-75）的几何意义

下面再讨论式（10-75）的几何意义。它可以写成（见图10-31）

它表示当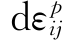不为零时，dσij必须指向加载面的外法线一侧，这就是加载准则，这时

如果dσij不指向外法线一侧，则只有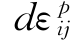=0才不违反上式。这就是卸载准则。

对于理想塑性材料，由于dσij不能指向外法线一侧，因此不论加载和卸载都有

（加载时AC与n垂直，卸载时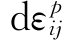=0）

早先人们不了解与加载面有什么关系，米塞斯在1928年类比了弹性应变增量可以用弹性位势函数对应力进行微分后所得的表达式，提出了塑性位势的概念.其数学形式是：

此处g是塑性位势函数，而上述公式称为塑性位势理论。在有了杜拉克公设以后，则在该公设成立的条件下，由式（10-76）必然得出g=f，一般将g=f的塑性本构关系称为与加载条件相关联的流动法则。

应该指出，由于屈雷斯加屈服准则是由几个方程分段表示的，其屈服轨迹为分段直线，各线段之间的交点是一个角点，没有唯一的法线方向。屈雷斯加屈服准则的这些特点对于相应的塑性应力—应变关系的建立带来很多不便，相关的应用也不多。因此，本书只针对米塞斯屈服准则等具有光滑屈服面的情况建立塑性应力—应变关系。

3.塑性变形的增量理论

增量理论又称流动理论，是描述材料处于塑性状态时，应力与应变增量或应变速率之间关系的理论，它是针对加载过程中的每一瞬间的应力状态来确定该瞬间的应变增量的，这样就撇开了加载历史的影响。

1）列维—米塞斯（Levy-Mises）方程

对于刚塑性材料，由于塑性变形时体积不变，应变增量张量就是应变增量偏张量，即

设材料符合米塞斯屈服准则，则将米塞斯屈服准则代入式（10-76），得

即应变增量与应力偏量成正比。式中dλ为一正的瞬时常数，在加载的不同瞬时是变化的，在卸载时dλ=0。

式（10-77）称为列维—米塞斯方程。是列维和米塞斯分别在1871年和1913年建立的。考虑到刚塑性变形时，比较式（10-77）与广义虎克定律式（10-63b），可见两者形式相似，仅比例系数不同。

上式可写成以下形式：

利用等比定理就可得到

或

上式表明应力莫尔圆和应变增量莫尔圆是几何相似的，只是原点位置不同。

比例系数dλ可按如下方法求得。将式（10-78）写成3个式子然后平方，得

再将式（10-77b）中i≠j的3个式子平方并乘以6，可得

将式（10-78c）和式（10-77c）两边相加，整理后可得

所以

其中，称为等效应变增量。

对于理想塑性材料，式中的，这时dλ的含义可参考图10-32来理解。

将式（10-79）代入式（10-77），并考虑到σm=（σx+σy+σz）/3，经整理后可得

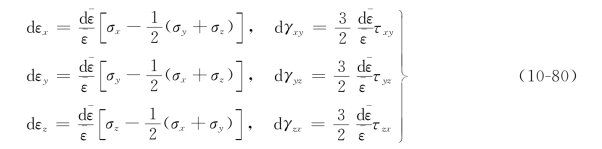
这与广义虎克定律式（10-60）的形式接近，前3式中的1/2就是体积不变时的泊松比。

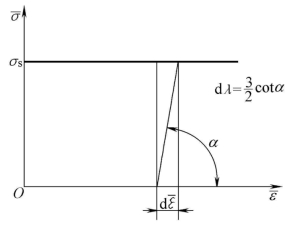
图10-32　dλ的涵义

下面我们利用米塞斯方程来证明上一章中指出过的一些结论：

（1）塑性平面变形时，如设z向没有变形，则有dεz=0，按体积不变条件有

(www.xing528.com)

将式（10-80）的前两式代入上式，有

由此可得

（2）在某些轴对称状态中，有dερ=dεθ，根据式（10-77）有，因此有σρ=σθ。

应指出，米塞斯方程仅适用于理想刚塑性材料，它只给出了应变增量与应力偏量之间的关系。由于dεm=0，因而应力球张量不能唯一确定。因此，如果已知dεij，则由式（10-77）或式（10-80）只能求得，而不能直接求得σij。这是刚塑性假设的一个弱点。另一方面，对于理想塑性材料，式（10-80）中的等于常数σs，而实际上是不定的，所以，如果已知σij，则由式（10-77）或式（10-80）只能求得dεij各分量之间的比值，而不能直接求出它们的实际数值。因此，对于理想刚塑性材料，应变增量与应力分量之间还不完全是单值关系，但在本书所讨论的范围内并不影响其使用。

2）应力—应变速率方程（圣维南塑性流动方程）

若将式（10-77（a））除以时间dt，可得

式中，即为应变速率张量；令，则上式即为

式中，。

式（10-81）中称为等效应变速率。卸载时。上式就是应力—应变速率方程，它同样可以写成

式（10-82）最早是由圣维南（Saint-Venant）于1870年提出的，它与牛顿黏性流体的牛顿公式很相似，所以也叫塑性流动方程。米塞斯方程实际上就是流动方程的增量形式，所以，如果不考虑应变速率对材料性能的影响，则两者是一致的。

3）普朗特—劳斯方程

普朗特和劳斯在米塞斯方程的基础上进一步考虑了弹性变形，他们认为，在塑性变形时，总应变增量dεij是塑性应变增量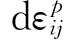及弹性应变增量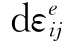之和，即

其中，和应力之间的关系可用米塞斯方程计算：

弹性应变增量可由式（10-64）微分得到，即

将以上两式代入式（10-69），即可得到普朗特-劳斯方程：

上式也可分别写成

分析上式可知，如dεij为已知，则应力张量σij是确定的，但对于理想塑性材料，仍然不能由σij求得确定的dεij值。对于硬化材料，变形过程每瞬时的dλ是定值，因此，劳斯方程中的dεij和σij之间完全是单值关系。

劳斯方程由于考虑了弹性变形，因此可以求解回弹及残余应力问题，但求解的难度远高于不考虑弹性变形的米塞斯方程。随着计算机技术的进步，劳斯方程在数值模拟中得到了广泛的应用。

增量理论表达了塑性变形中各瞬时应变增量或速率与应力的关系，通过对各瞬时段变形的累加可以得出各种应变路径下的整个变形过程。因此，增量理论能够反映加载过程的历史对变形的影响，对于各种塑性变形条件都是普遍适用的。但要注意，对于大变形问题，要采用有限应变。

4.塑性变形的全量理论（形变理论）

在简单加载时，也即各应力分量按同一比例增加时，应力主轴的方向将固定不变。由于应变增量的主轴是和应力主轴重合的，所以它的主轴也将始终不变，这种变形也称简单变形。这种条件下，可以对劳斯方程进行积分得到全量应变和应力之间的关系，叫做全量理论。

我们可用以下的式子表示简单加载：

式中，——初始应力状态；

　　　C——变形过程中的单调增函数。

对于理想塑性材料，塑性变形阶段的C为常数。

于是劳斯方程式（10-85）的第一式可写为

在小变形情况下，dεij的积分就是小应变张量εij，故对上式积分即得

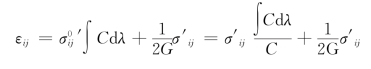
如设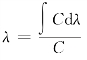，则由式（10-85）积分所得到的全量关系为

上式最早是由汉基于1924年提出的，所以叫做汉基方程。汉基方程没有考虑硬化，因此系数λ中所包含的函数C在塑性变形时是常数，于是

将式（10-86）与广义虎克定律作一对比，将有助于对汉基方程的理解。如果我们引入一个符号G'（它也可叫做塑性剪切模量），使得

则式（10-86）的第一式即可写成

于是式（10-86）和广义虎克定律的表达式（10-62）和式（10-63b）在形式上是一样的。通过与推导式（10-79）dλ同样的推导方法，由上式可以得到

同样，由广义虎克定律的式（10-63（b））也可得到

对于理想塑性材料，λ、G'、G的涵义都可以从图10-33（b））所示的曲线上表示出来。对于硬化材料，则如图10-33（b）所示。从图中可以看出，G'和G的涵义很相似，区别仅在于弹性剪切模量G是材料常数，而G'则随变形过程而变。所以我们可以把小变形全量理论看成是广义虎克定律在小塑性变形中的推广。而且小变形全量理论中也已经包含了广义虎克定律。

图10-33　λ、G、G'的几何意义

1945年前后，伊留辛（А.Ильюшин）发展了汉基理论，把它推广到硬化材料。而且他证明了在满足下列条件时，可保证物体内每个质点都是简单加载：

①塑性变形是微小的，和弹性变形属于同一个数量级；

②外载荷的各分量按比例增加，即；

③曲线符合单一曲线假设，且呈幂函数形式，即。

伊留辛发展了的小变形理论在解决小弹塑性变形问题中得到了广泛的应用。

如果假定材料是刚塑性的，则式（10-86）中的，就是米塞斯方程在小变形时的积分形式。

考虑到塑性变形时体积不变，，上式也可写成如下形式：

上式与米塞斯方程的式（10-80）、流动方程的式（10-82）乃至广义虎克定律的式（10-60）等在形式上都是非常相似的。

对于大塑性变形，纳达依在简单加载条件下由米塞斯方程的积分得到了大塑性变形的全量关系，并考虑了变形硬化。但是在大塑性变形条件下，除了少数接近理想状态的场合外，一般难于保证简单加载。因此，大塑性变形全量理论的应用受到了很大的限制。

通过以上分析可知，在上述各种理论中，劳斯方程是普遍适用的；在弹性变形可以忽略的情况下，米塞斯方程和塑性流动方程也是普遍适用的。它们也可以推广到硬化材料。全量理论则是增量理论在简单加载条件下的积分，所以在一般情况下不能普遍适用。在塑性成形中，由于难以保证简单加载，所以—般都采用增量理论，其中主要是米塞斯方程或流动方程。但应指出，塑性成形理论中很重要的问题之一是求变形力，这时一般只需研究变形过程中某一特定瞬间的极其短暂的变形，如果我们以变形体在该瞬时的形状、尺寸及性能作为原始状态，那么小变形全量理论和增量理论可以认为是一致的，所以在有些文献中，就使用小变形全量理论的表达式进行运算。

5.塑性应力应变关系的实验验证

罗代于1926年最早用试验来验证塑性应力应变的关系。他引入了应力参数μσ（见式（10-13））及应变参数με：

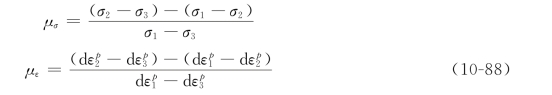
按前述的增量理论，有如下关系：

由此可得μσ=με（见图10-34中的实线），这一关系可用试验方法来验证。试验方法与验证屈服准则的方法相似，但由于dεij是测不出来的，需要用εij代替dεij，所以必须简单加载。试验结果如图10-34中的虚线所示，试验数据基本符合理论值，但存在系统的偏差。后来，有的试验者用更好的方法消除材料各向异性的影响，证实前述方程是足够精确的。

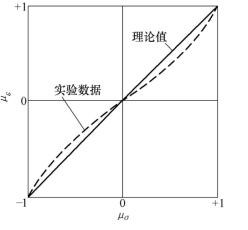
图10-34　塑性应力应变关系的实验验证

6.最大散逸功原理

如前所述，—种应力状态σij可以用主应力空间中的矢量来表示，塑性变形时，该矢量的端点一定在屈服表面上。同样，应变增量dεij也可以用主应变空间里的矢量来表示。由于应变增量的主轴与应力主轴是重合的，故它们可以画在同一主轴空间内。

由于塑性变形时，

所以表示dεij的矢量OQ一定在π平面上。设应力矢量OP0在π平面上的投影为OP（见图10-35），则OP即可代表应力偏张量。现在我们将矢量OQ的起点移至OP的端点，变成PQ。这样，单位体积塑性功增量就是矢量OP与PQ的数量积：在这里，我们假定应力σij满足米塞斯屈服准则，于是P点即在米塞斯圆上。同时，假设应力与应变符合米塞斯方程，于是，与dεij成正比，故矢量PQ的方向一定与OP相同。可见，代表应变增量的矢量PQ必然垂直于P点处的屈服轨迹。

与前述的σij符合同一屈服准则，但不一定与前述dεij符合应力—应变关系的应力状态是很多的。我们用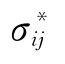表示这样的应力状态，并用π平面上的矢量OP*代表其应力偏张量（见图10-35）。将σ*'ij与前述的dεij相乘，同样可得到一个单位体积塑性功增量：

将式（10-89）减去式（10-90），可得（见图10-35）

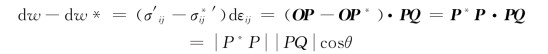
由于：①屈服轨迹是外凸的曲线，P*点一定在P点处屈服轨迹切线MN的左边；②PQ垂直于P点处的屈服轨迹，所以，θ≤π/2，cosθ≥0，由此得

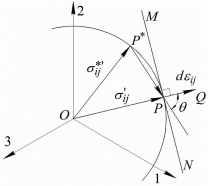
图10-35　π平面上的偏应力矢量及应变矢量

将上式对整个体积积分，可得

对上式可作如下的表述：对于一定的应变增量场而言，在所有符合屈服准则的应力场中，与该应变增量场符合应力—应变关系的应力场所做的塑性功最大。如果与符合应力应变关系的应变增量场为，这时代表的矢量也必然垂直于矢量端点处的屈服轨迹，于是同样存在如下关系：

将上述原理应用于实际变形。设dεij为真实应变增量场，则真实应力场σij必然与dεij符合应力-应变关系，于是由式（10-91）可知，它们所做的塑性功，相对于虚拟的或可能的应力场而言，总是最大的。也就是说，由于屈服准则的限制，物体在塑性变形时，总是要导致最大的能量散逸（或称能量消耗）。因此，上述原理就叫最大散逸功原理，它的具体应用见下一章。