1.广义虎克定律
在单向应力状态下,弹性变形时应力与应变之间的关系,由虎克定律表达,即
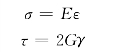
对于一般应力状态下的各向同性材料的应力与应变之间的关系,则由广义虎克定律表达,即
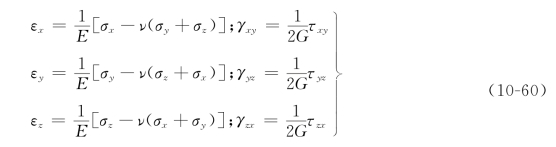
式中,E——弹性模量;
ν——泊松比;
G——切变模量。
3个弹性常数E、v、G之间有以下关系:

若将式(10-60)中的3个等式相加整理后可得
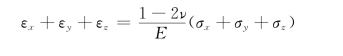
即

式(10-62)表明,物体弹性变形时其单位体积变化率θ(θ=3εm)与平均应力成正比,说明应力球张量使物体产生弹性的体积改变。
若将式(10-60)中的前三式分别减去式(10-62),例如:
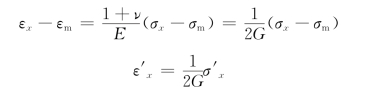
即
可得3个式子,将这3个式子与式(10-60)中的后三式合并,可写成如下形式:
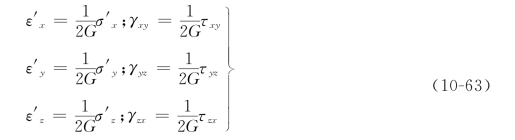
简记为
![]()
上式表示应变偏张量与应力偏张量成正比,即表明物体形状的改变只是由应力偏张量引起的。
由上一章可知,应变张量可以分解为应变偏张量和应变球张量:
![]()
将式(10-62)及式(10-63(a))代入上式,就可得到广义虎克定律的张量形式:
![]()
2.应变能
若物体在外力作用下产生弹性变形,设物体保持平衡且无温度变化,则外力所做的功将全部转换成弹性势能(位能)。弹性位能可以通过应力所做的功来计算。
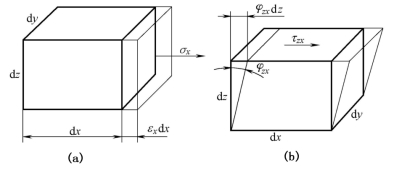
如图10-25(a)所示,设一单元体在应力作用下发生弹性变形,单元体棱长为dx、dy及dz,它在x方向的正应变为εx,考虑到应力随应变线性增长,正应力分量σx所作的功为
![]()
 (https://www.xing528.com)
(https://www.xing528.com)
图10-25 单元体应力与变形的示意
(a)σx所作的功;(b)τzx所作的功
单位体积的弹性位能为
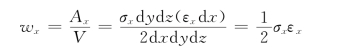
同样,如图10-25(b)所示,剪应力分量τzx对单位体积所作的弹性功为
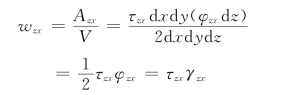
其他应力分量所作的变形功也可同样处理。由此,单元体单位体积的变形功(即弹性位能)为
![]()
单位体积内总的弹性位能w可以分解为体积变化位能wV和形状变化位能wφ(弹性形变能),即

为了计算方便,选用主轴为坐标轴,则
![]()
将广义虎克定律式(10-60)代人式(10-65a),整理后得
![]()
单位体积的体积变化位能(由应力球张量引起)为
![]()
式中,![]() 又可用式(10-60)代入,将式(10-65c)简化为
又可用式(10-60)代入,将式(10-65c)简化为
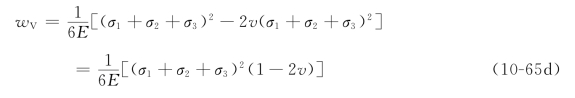
将式(10-65c)、式(10-65d)代入式(10-65b),整理后得
![]()
将式(10-65e)与米塞斯屈服准则比较,若满足屈服准则,则有
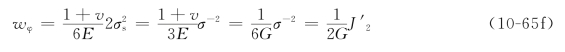
式(10-65f)说明,单位体积的弹性形变能wφ达到常数![]() 时,该材料(质点)就开始进入屈服状态,故将米塞斯屈服准则简称为能量准则或能量条件。
时,该材料(质点)就开始进入屈服状态,故将米塞斯屈服准则简称为能量准则或能量条件。
设变形体体积为V,则整个变形体的弹性位能为
![]()
另外,当材料产生塑性应变增量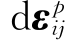 时,考虑到时间dt内应力可以视为常量,故单位体积的塑性变形功增量dw可以由下式计算:
时,考虑到时间dt内应力可以视为常量,故单位体积的塑性变形功增量dw可以由下式计算:
![]()
由于塑性应力—应变关系是非线性的,单位体积的塑性变形功w只能通过对dw的积分求得

由于塑性变形中体积不变,应力球张量不作功,上式又可以写成
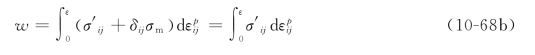
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




