表达真实应力-应变曲线的公式优化

试验所得的真实应力—应变曲线一般都不是简单的函数关系。为了实际应用，常希望能将此曲线表达成某一函数形式。最简单的函数关系仅将真实应力表达为真实应变的函数，这在分析常温下的塑性成形问题时是合适的，但在温成形和热成形问题的分析中，还应该考虑变形温度和速度的影响。

1.应变硬化

当只考虑应变硬化时，根据对真实应力—应变曲线的研究，可将它归纳成4种类型，如图10-24（a）、（b）、（c）、（d）所示。

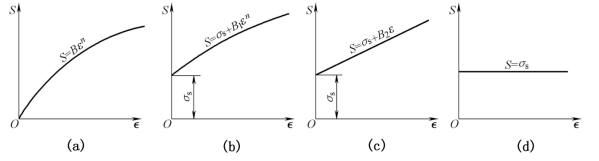
图10-24　真实应力—应变曲线的基本类型

1）幂函数方程

很多金属的真实应力—应变曲线近似于抛物线形状，对于立方晶格的退火金属（如铁、铜、铝等），其真实应力—应变曲线可相当精确地用以下幂函数形式表示（见图10-24（a））：

式中，K——与材料有关的常数，称为硬化系数；

　　　n——硬化指数。

K与n的数值可从各种材料手册中查到，也可按如下方法由拉伸失稳点的真实应力Sb和对数应变∈b求得。

对式（10-47）求导数，得

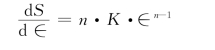
因在失稳点b处，故根据式（10-44），有

因

所以从以上两式可求得

代入式（10-48），即得

于是K、n值可由Sb、∈b求得。式（10-47）也可写成

这种函数形式应用很广，但还有一些不足，如在塑性变形量很大时，许多金属材料的硬化会逐渐减慢，直至停止，即达到饱和，而幂函数不能描述硬化饱和现象。因此，对于在塑性变形量很大的场合，可以采用如下Voce形式的硬化函数：

其中，A为饱和应力，B、C为材料常数；采用此函数，虽然真实应力仍将随着真实应变的增加而提高，但不会超过饱和应力A。

另外，在弹性阶段，应力—应变之间为线性函数关系，屈服后才呈曲线关系。弹性阶段的直线与上述函数曲线应该在屈服点相交。但由于幂函数中的各个参数是通过函数曲线与实验曲线的拟合得到的，使得这个交点处的应力并不等于屈服应力。可以采用下述Swift形式的硬化函数使交点与屈服点重合：

(https://www.xing528.com)

其中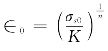，称为初应变。

2）刚塑性材料的幂函数方程

对于有初始屈服应力σs的冷变形金属材料，可较好地表达为

这时曲线直接由S轴上的σs作出（见图10-24（b））。这里略去了弹性变形阶段，因为对大塑性变形来说，略去弹性变形，不影响其精确性。式中的K1、n两参数需根据实验曲线求出。

3）线性硬化方程

有时为了简单起见，可将真实应力—应变曲线视作直线，其表达式为

这一直线是硬化曲线的简化，故也称之为硬化直线。式中，（见图10-18）。

4）理想塑性

对于几乎不产生硬化的材料，可认为真实应力—应变曲线是—水平线，如图10-24（d）所示。这时的表达式为

在室温下，只有纯度极高的铅可认为不产生加工硬化。高温下的钢，也可采用这一无硬化的假设。

2.考虑应变速率和变形温度的影响

如图10-23所示，随着变形温度的提高，金属材料的应变硬化减弱，其流动应力随着应变速率的增加而提高，这种性质称为黏性。黏塑性材料的流动应力是应变、应变速率和温度的函数，下面两种工程中常用的真实应力表达式考虑了应变速率的影响。

1）Backofen模型

式中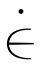，——应变速率；

　　　k——材料常数；

　　　m——应变速率敏感指数。

超塑性材料的真实应力就是采用这种模型描述的。

2）Rosserd模型

可见，它是式（10-47）和式（10-57）的综合，同时考虑了应变和应变速率对真实应力的影响。

热成形时真实应力随温度的升高而降低，因此可以在式（10-58）中引入温度的影响因素，将它修改为

式中，T——温度；

　　　c——材料常数。