应变硬化及其后继屈服行为

以上所讨论的屈服准则只适用于各向同性的理想塑性材料。对于应变硬化材料，可以认为其初始屈服时服从前述的准则。当材料产生应变硬化后，屈服准则将发生变化，在变形过程中的每一时刻，都将有一后继的瞬时屈服表面和屈服轨迹。这种后继屈服表面和轨迹，也称加载表面（轨迹）。

后继屈服轨迹的变化是很复杂的，通常采用的几种假说都只是近似地反映了其主要特点。以下介绍常用的3种硬化假说。

1.各向同性硬化

目前最常用的硬化假说是各向同性硬化假说，也称为等向强化模型，其要点是：

（1）材料在硬化后仍然保持各向同性。

（2）硬化后屈服轨迹的中心位置和形状保持不变，它们在π平面上仍然是以原点为中心的对称封闭曲线，但其大小则随变形的进行而不断地扩大。如材料初始屈服时服从米塞斯或屈雷斯加屈服准则，则后继屈服轨迹就是一系列同心圆或正六边形（见图10-13）。这时屈服表面也在不断均匀扩大。

如把前述屈服准则统一写成f（σij）=C的形式，则屈服轨迹（或屈服表面）的中心位置和形状就由函数f（σij）决定，而常数C则决定轨迹的大小。因此，根据上述假说，各向同性硬化屈服准则可以用同样的函数表示，只是为与初始屈服准则相区别而加上星号作为上标，即表示为f*（σij），然后只要将等号右边的常数C改成随变形而变的变量就行了。假设这一变量用Y表示，于是各向同性硬化的屈雷斯加和米塞斯屈服准则分别为

或

关于Y的变化规律，目前有两种假设。第一种叫做单一曲线假设，即认为对于任一种材料而言，单向应力状态下的真实应力—真实应变曲线与复杂应力状态下的等效应力—等效应变曲线是一致的。根据这种假设，Y只是等效应变¯ε的函数，这一函数只取决于材料的性质而与应力状态无关，因此可用单向拉伸等比较简单的试验来确定，这时，Y实际上就是流动应力S（参看10.2节）。这种假设在简单加载以及某些非简单加载条件下已被证明是正确的。由于这种假设的使用比较方便，所以，尽管它还不能为更多的试验所证实，但仍得到广泛的应用。第二种假设是“能量条件”，它认为材料的硬化程度只取决于变形过程中的塑性变形功，而与应力状态及加载路线无关。因此，Y是塑性功的函数。这一假设得到了更多的实验证明，具有更为一般的性质，但比较复杂，使用不够方便。

图10-13　各向同性硬化材料的后继屈服轨迹

2.随动硬化

设对于某种硬化材料，在一个方向（例如拉伸）加载使之进入塑性以后，在σ=σr1时卸载，并反方向（压缩）加载，直至材料进入新的塑性屈服状态。由于存在包辛格效应，反向屈服应力通常在数值上既不等于材料的初始屈服应力σs0，也不等于卸载时的应力σr1，如图10-14所示。当σr1-σs11=2σs0时，该用材称为随动硬化材料；当时，该用材称为各向同性硬化材料。如果处于上述情况之间，即，同时，则称材料为混合硬化材料。

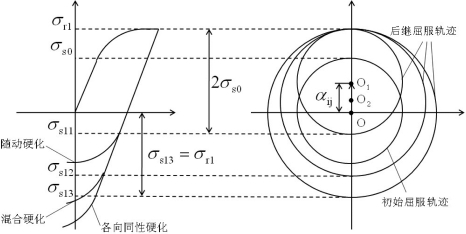
图10-14　反向加载与后继屈服轨迹

图10-14还显示了π平面上后继屈服轨迹的变化。假定加载是沿竖直向上的方向，前面已经述及，各向同性硬化材料的后继屈服轨迹是保持形状和中心不变而均匀地扩大，其半径由σs0增大为σr13；随动硬化材料的后继屈服轨迹保持形状和大小不变，在主应力空间作刚体移动，其中心的移动量为αij；混合硬化材料的后继屈服轨迹仅保持形状不变，其大小和中心均发生变化，变化的幅度介于前二者之间。(www.xing528.com)

随动硬化后继屈服函数可表示为

其中，αij称为背应力，是加载曲面的中心在应力空间的移动张量。它与材料硬化特性以及变形历史有关。中心的移动规律可以用普拉格（Prager）随动硬化法则计算。

普拉格假设后继屈服曲面中心的移动是沿屈服表面上加载应力点处的法线方向的，如图10-14所示。采用米塞斯屈服条件时，普拉格随动硬化法则的后继屈服函数是

其中，。

对于单调加载情况，随动硬化法则与各向同性硬化法则是等价的。如果发生卸载和反向屈服，例如对冲压后回弹的工件，则各向同性硬化法显然过高地估计了反向屈服应力，导致产生明显的误差；这时可采用随动硬化法则，它适合于σr1-σs1=2σs0的材料。

3.混合硬化法则

一般材料的后继屈服轨迹既有大小的变化，也有中心的移动。哈奇（Hodge）将各向同性硬化和运动硬化两种法则综合考虑，提出了混合硬化法则。

混合硬化的后继屈服函数可以表示为

其中；M表示各向同性硬化特性在全部硬化特性中所占的比例，称之为混合硬化参数。一般取M=0～1，如令M=1或M=0，混合硬化法则就分别蜕化为各向同性硬化法则和随动硬化法则。

类似于随动硬化法则，混合硬化法则主要用于发生反向加载的情况。

实际的后继屈服轨迹比上述简化模型更为复杂。图10-15为艾维（1vey）对铝合金薄管作拉扭实验的屈服轨迹，可见，当应力点向正τ方向加载时，整个屈服面向正τ方向移动，表现出明显的包辛格效应，加载面形状也有明显的变化。所以以上介绍的几种硬化模型仍然是近似的简化模型。

图10-15　铝合金薄管拉扭实验的后继屈服轨迹

（引自Ivey，H.J.J.Mech Eng Sci，1961（3）：15）