实验验证屈服准则

自1926年以来，用实验来验证屈服准则的工作一直在进行。实验的方法是多种多样的，最普通的方法是用各种金属薄壁管承受复合载荷（例如，拉伸与扭转、拉伸与弯曲或者拉伸与内压复合等），实验的要求都非常严格。下面只简单介绍薄壁管承受拉扭复合载荷的实验。

薄壁管拉扭组合作用下可以认为处于平面应力状态，承受均匀的拉应力σ及剪应力τ（见图10-9）。根据图中P点的应力分量，可以用应力莫尔圆求得主应力：

图10-9　薄壁管复合拉扭试验

将它们代入屈雷斯加准则的式（10-4）得

可写成

将上列主应力代入米塞斯准则的式（10-9），可得

或(www.xing528.com)

式（10-23）及式（10-24）就是（σ/σs）—（τ/σs）坐标平面上的屈服轨迹，它们都是椭圆，如图10-10所示。

图10-10　（σ/σs）-（τ/σs）平面上的屈服轨迹

图10-11　¯σ-¯ε试验曲线及假想屈服点

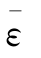试验前应极其仔细地准备试样，尽可能做到各向同性，并测得拉伸屈服应力σs。试验时先加一定的扭矩，使材料产生剪应力τ，然后不断增加拉力，亦即按图10-10中的OAB路线加载，直至明显屈服。加拉力后即连续记下载荷、扭角及伸长量，并换算成σ、γ及ε，算出相应的及，作出-曲线，并用图10-11所示的方法求得假想屈服点。根据屈服时的σ/σs及τ/σs值，即可在图10-10中记下—点。下次试验可按图10-10中的OCD路线加载，又可得到一点。这样连续试验，即可记下许多屈服点，它们的连线就是试验的屈服轨迹。

1931年，泰勒（TayIor）及奎乃（Quinney）用钢、铜、镍的薄壁管进行了拉扭复合试验，结果如图10-12所示。大量试验表明，韧性金属材料的实验数据点大多很接近米塞斯椭圆。因此，米塞斯屈服准则是比较符合实际的。

图10-12　泰勒及奎乃实验结果

1—米塞斯准则；2—屈雷斯加准则