屈服准则的几何表达：屈服轨迹和屈服表面

屈服准则的数学表达式可以用几何图形形象化地表示出来。在σ1σ2σ3坐标系中，屈服准则都是空间曲面，叫做屈服表面。如把屈服准则表示在各种平面坐标系中，则它们都是封闭曲线，叫做屈服轨迹。屈服表面和屈服轨迹是进一步分析屈服准则的有力工具。

1.二向应力状态的屈服轨迹

以σ3=0代入式（10-8）即可得到两向应力状态的米塞斯屈服准则：

上式在σ1σ2坐标平面内是一个椭圆（见图10-2），它的中心在原点，对称轴与坐标轴（即主轴σ1、σ2）成45°，长半轴为，短半轴为，与原坐标轴的截距为±σs。这个椭圆就叫σ1σ2平面上的米塞斯屈服轨迹。

同样，以σ3=0代入式（10-5），可得两向应力状态时的屈雷斯加屈服准则：

这是—个六边形，内接于米塞斯椭圆（见图10-2），称为屈雷斯加六边形。

由于任一个二向应力状态都可用σ1σ2主应力坐标平面上的一点P来表示，并可用矢量OP来代表。因此，屈服轨迹的几何意义是：若P点在屈服轨迹里面，则材料的质点处于弹性状态；若P点在屈服轨迹上，则该质点处于塑性状态。对于理想塑性材料，P点不可能在屈服轨迹的外面。

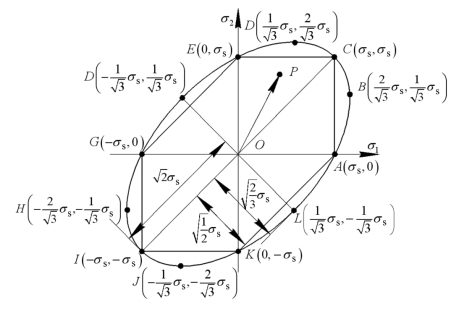
图10-2　二向应力状态下的屈服轨迹

屈雷斯加六边形内接于米塞斯椭圆，这就意味着，在6个角点上，两个屈服准则是一致的。其中与坐标轴相交的A、E、G、K等4点表示单向应力状态；与椭圆长轴相交的2个点C、I为轴对称应力状态，其特征是σ1=σ2。除这6点外，两个准则都不一致。米塞斯椭圆在外，意味着按米塞斯屈服准则需要较大的应力才能使材料（质点）屈服。两个屈服准则差别最大的也只有6个点（B、D、F、H、J、L）。其中，F、L两点的特征是σ1=-σ2，即纯剪状态。另4点B、D、H、J的特征是σ1=2σ2或2σ1=σ2，因为σ3=0，σm，故为平面应变状态。在这6个点上，两个屈服准则的差别都是15.5%。

2.主应力空间中的屈服表面

以主应力为坐标轴可以构成—个“主应力空间”，如图10-3所示。一种应力状态（σ1，σ2，σ3）即可用该空间中的一点P来表示，并可用矢量OP来代表。设ON为该空间第一象限的等倾线。由P点引一直线PM⊥ON，并把矢量OP分解成OM及MP，则OM表示应力张量中的球张量，而MP表示应力偏张量。等倾线ON有这样的特点：在垂直于ON的平面上，任何点的应力球张量都相同；在平行于ON的直线上，各点的应力偏张量都相同。下面讨论如何在主应力空间中表示屈服准则。

由于矢量

所以矢量的模

其中

而就是σ1、σ2、σ3在ON线上的投影之和，考虑到ON的方向余弦为l=m=n=1/3，于是

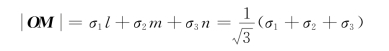
由此得

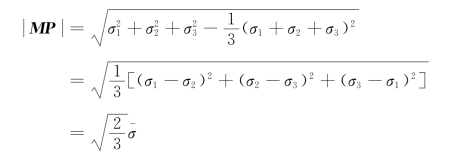
根据米塞斯屈服准则，当¯σ=σs时材料就屈服，故当时材料就屈服。由于垂直于ON线的平面上所有的点都具有相同的球张量，而球张量又不影响屈服，所以，若以M为圆心，以为半径，在垂直于ON线的平面上作一圆，则该圆上各点的应力偏张量均相等，即均为，所以圆上各点都进入屈服状态。又由于平行于ON的直线上所有的点都有相同的偏张量，所以，以ON为轴线，以为半径作一圆柱面，则此圆柱面上的点都满足米塞斯屈服准则。这个圆柱面就是主应力空间中的米塞斯屈服表面（见图10-4）。同理，屈雷斯加屈服准则的表达式（10-5），在主应力空间中的几何图形是一个内接于米塞斯圆柱面的正六棱柱面，称为屈雷斯加屈服表面（图10-4）。

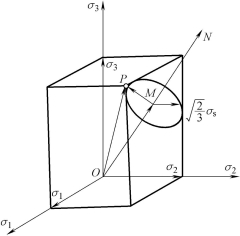
图10-3　主应力空间

屈服表面的几何意义是：若主应力空间中一点应力状态矢量的端点（P点）在屈服表面内部，则该点处于弹性状态；若P点位于屈服表面，则该点处于塑性状态。对于理想塑性材料，P点不能在屈服表面之外。

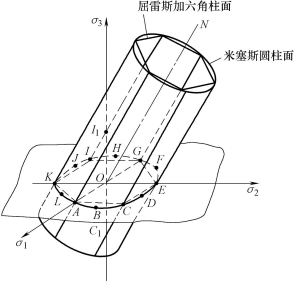
图10-4　主应力空间中的屈服表面

实际上前面图10-2所示的屈服轨迹就是上述屈服表面与σ1Oσ2平面的交线。图10-2中的12个特征点在屈服表面上就成了柱面的母线。其中，通过A、C、E、G、I、K等6点的母线就是六棱柱面的棱，它们都与坐标轴相交。所以，这6条母线上的点实际上都代表叠加了不同静水压力σ0的单向屈服应力状态：

通过A及G点的母线为（σ0±σs，σ0，σ0）；

通过E及K点的母线为（σ0，σ0±σs，σ0）；

通过C及I点的母线为（σ0，σ0，σ0±σs）。

它们共同的特点是有两个主应力相等。这就是说，对于有两个主应力相等的应力状态，两个准则是一致的，而单向应力状态和—部分轴对称状态正是属于这种情况。两个屈服准则相差最大的6条母线上的点，实际上都是纯剪状态（即一个主应力为零，另两个主应力数值相等，符号相反）叠加了不同的静水压力，它们的共同特点都是；一个主应力是另外两个的平均值，这正是平面变形状态的特征。所以，平面变形时，两个屈服准则相差最大。

3.π平面上的屈服轨迹

在主应力空间中，通过坐标原点并垂直于等倾线ON的平面称为π平面，其方程为

π平面与两个屈服表面都垂直，故屈服表面在π平面上的投影（也即为交线）是半径为的圆及其内接正六边形，这就是π平面上的屈服轨迹，见图10-5。

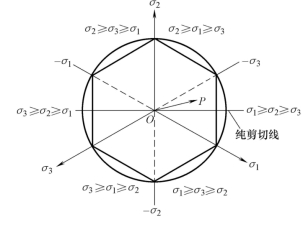
图10-5　π平面上的屈服轨迹

由于π平面是通过坐标原点并与等倾线ON垂直的平面，则该面上σm=0，即没有应力球张量的影响，平面上任何一个应力矢量均表示应力偏张量。因此，π平面上的屈服轨迹更清楚地表示出屈服准则的性质。

3根主轴在π平面上的投影互成120°角，如果把主轴负向的投影也画出来，就把π平面等分成6个60°角的区间，每个区间内应力的大小次序互不相同。3根主轴线上的点都表示（减去了球张量的）单向应力状态。每个60°角的平分线上的点都表示纯剪应力状态。由于6个区间的屈服轨迹是一样的，所以，实际上只要用一个区间（如图10-5中的σ1≥σ2≥σ3区间）就可以表示出整个屈服轨迹的性质。

4.中间主应力的影响

下面进一步讨论两个屈服准则的差别。设若σ1≥σ2≥σ3，则屈雷斯加屈服准则可写成

这时，中间主应力σ2可以在σ2=σ1到σ2=σ3之间任意变化而不影响材料的屈服，但在米塞斯屈服准则中σ2是有影响的。为了评价其影响，应先找到一个能表征中间主应力变化的参数，此参数不应受应力球张量的影响。由第9章可知，三向应力莫尔圆的3个半径就是3个主剪应力，它们和球张量无关。如σ1和σ3不变，则大圆的半径不变，而两个小圆的半径将随σ2而变，所以，我们可以用中间两个小莫尔圆的半径之差与大圆半径的比值作为表征中间主应力变化的参数，用μσ表示。该参数是由罗代（W.Löde）提出的，叫做罗代应力参数，即

当σ2在σ1至σ3之间变化时，μσ将在+1至-l之间变化。

为了便于比较，我们利用μσ将米塞斯屈服准则改写成类似于屈雷斯加屈服准则的形式。由式（10-13a）可以解得

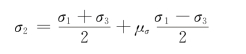
代入式（10-9），整理后得

若设

则式（10-13b）即可写成

式中的β的变化范围为1～1.155，如图10-6及表10-1所示。

表10-1

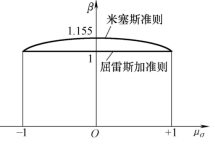
图10-6　β和μσ的关系

屈雷斯加准则相当于式（10-15）中β≡1的情况，即如图10-6中的水平线所示。这样，两个屈服准则及中间主应力的影响就可看得很清楚了。其中，单向应力叠加球张量时，两个准则是一致的；若为平面应变，也即纯剪叠加球张量时，两个准则相差最大，为15.5%。(www.xing528.com)

由以上分析可知，只要采用不同的β值，式（10-15）也可成为两个准则的统一表达式。这种表达式还可以写成另一种形式。式（10-15）中等号左边的σ1-σ3就等于屈服时的最大剪应力的2倍。如以符号K表示屈服时的最大剪应力，则

于是，式（10-15）即可改写成

式中，按屈雷斯加屈服准则，K≡σs/2，按米塞斯准则，则K=（0.5～0.577）σs。

5.平面问题和轴对称问题中屈服准则的简化

在平面问题和轴对称问题中，一些应力分量或为零或为常数，故屈服准则的表达式可得到某些简化。

对于米塞斯屈服淮则，其通式为式（10-9）或式（10-10）。用圆柱坐标时，将其中的下角标x、y换成r、θ。

平面应力时，令σz=σ3=τzx=τzy=0，故上两式简化为式（10-11），即

或

平面应变时，令τzx=τzy=0，σ1、σ2为塑性流动平面内的主应力，故σz=（σx+σy）/2=（σ1+σ2）/2，则式（10-9）及式（10-10）简化为

或

研究轴对称问题时，τrθ=τθz=0，故以主应力表示的米塞斯准则与式（10-9）没有不同，但式（10-10）则可简化为

在特殊情况下，如σ1=σ2或σr=σθ，则为

或

对于屈雷斯加准则，在平面变形以及已知主应力异号的平面应力状态下，都可以直接用xy平面上的应力分量表示：

例题10-1 一两端封闭的薄壁圆筒，半径为r，壁厚为t（设t<<r），受内压力p的作用（见图10-7），试求此圆筒产生屈服时的内压力p（设材料单向拉伸时的屈服应力为σs）。

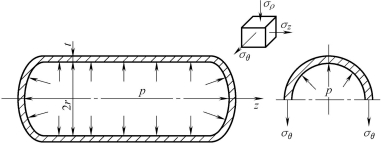
图10-7　受内压的薄壁圆筒

解：先求应力分量。取长度为l的一段圆筒，通过轴线建立圆柱坐标系，各应力分量如图10-7所示。

如图10-8所示，在圆筒壁上任取一微元面积ldAk，设作用在该微元面积上的法向力为dPn，则

dPn沿竖直方向的分力为

即

另一方面，上式右端的ldAkcosα即是微元面积ldAk在水平方向的投影面积ldA，即ldA=ldAkcosα。于是有dP=pldA

由此可见，对于受正压力作用的微元表面，不管其空间方位如何，由正压力产生的合力沿某指定方向的分量，可以用该微元表面在与该给定方向相垂直的平面上的投影面积，乘以正压力来确定。采用该投影法则，可以简化计算。

正压力对图10-8中半圆柱面的合力，可以通过对投影面的积分得到：

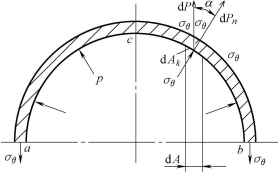
图10-8　法向应力的投影计算

由于内压力p为常数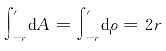，，所以

由竖直方向力的平衡条件P=2σθlt，得

于是

同理可求得

由以上两式可以看出，当t<<r时，σθ>>p，σz>>p，而，即与σθ和σz相比，σρ可以忽略，故可视为平面应力问题，于是可令σρ=0。即有

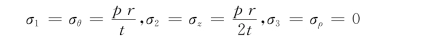
（1）由米塞斯屈服准则得

则

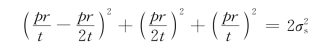
可求得

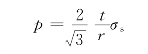
（2）由屈雷斯加屈服准则得

即

所以可求得