应变增量和应变速率张量的特性与应用

前面所讨论的是小应变，反映单元体在某一变形过程或变形过程中的某个阶段结束时的应变，称为全量应变。而塑性成形问题一般都是大变形，且大塑性变形的整个过程十分复杂。因此，前面讨论小应变时的这些公式在大变形中就不能直接应用。然而，大变形是由很多瞬间的小变形累积而成的，有必要分析大变形过程中某个特定瞬间的变形情况，这就需要提出应变增量和应变速率的概念。

1.速度分量和速度场

物体变形时，体内各质点都在运动，因此在变形过程中的每一时刻，物体内都存在一个速度场。前面讨论全量应变时，只是用了某变形过程终了时的位移场，所以没有引入时间参数。在描述整个变形过程时，则必须引入时间参数，这时的位移分量为

式中，x，y，z是物体中一点在某时刻的坐标，它也是时间的函数。所以，位移分量ui对时间的全导数就是该点的移动速度分量，一般以表示，可记为

小变形时，很小，全导数中的牵连部分可忽略不计，于是有

对于变形过程中的某一瞬时，即t为某定值时为坐标的连续函数，可确定一瞬时速度场。

2.位移增量和应变增量

物体在变形过程中，在一个极短的时间dt内，任一质点发生的极小的位移变化量称为位移增量，记为dui。在图9-25中，设物体中某一点P，它在变形过程中经PP'P1的路线到达P1，这时的位移为PP1，将PP1的分量代入几何方程求得的应变就是该变形过程的全量应变。若在某一瞬时，该点移动至PP'P1路线上的任一点，例如P'点，则由PP'求得的应变就是该瞬时的全量应变。如果该质点由P'再沿原路线经极短的时间dt移动无限小的距离到P″，这时位移矢量PP″与PP'之差即为此时的位移增量。

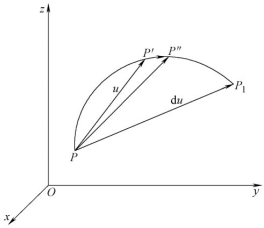
图9-25　位移矢量和增量

设此时的速度分量为，在随后的时间间隔dt之内，物体内各点的位移增量的分量为

根据前面小应变分析，产生位移增量后，变形体内各质点就有相应的无限小的应变增量，用dεij表示。通俗地说，以物体在变形过程中某瞬时的形状尺寸为原始状态，在此基础上发生的无限小应变就是应变增量。由于在极短的时间内所产生的位移增量（dui）与相应的应变增量（dεij）都是十分微小的，故可看作是小应变。此时位移增量与应变增量之间的关系，也即几何方程，形式上与小应变几何方程相同，只要将dui代替ui，dεij代替εij即可，于是得

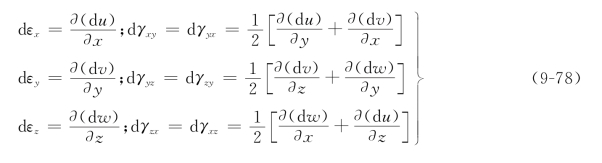
简记为

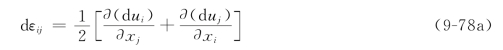
一点的应变增量也是二阶对称张量，称为应变增量张量：

应变增量是塑性成形理论中最常用的概念之一，因为在塑性变形加载过程中，质点在每一瞬时的应力状态一般是与该瞬时的应变增量相对应的，所以在分析塑性加工时，主要用应变增量。但应指出，塑性变形过程中某瞬时的应变增量dεij，是当时具体变形条件下的无限小应变，而当时的全量应变则是该瞬时以前的变形积累的结果。该瞬时的变形条件和以前的变形条件不一定相同，所以应变增量的主轴与当时的全量应变主轴不一定重合。(www.xing528.com)

应变增量张量和小应变张量一样，具有3个应变增量主方向、3个主应变增量（dε1、dε2、dε3）、3个不变量、3对主切应变增量、应变增量偏张量、应变增量球张量、等效应变增量，等等。它们的定义和表达式的形式与小应变张量一样，只需用dεij代替εij即可。记d（εij）=εij（t+Δt）-εij（t），则式中εij（t）和εij（t+Δt）都是以初始状态为参考状态计算的全量应变，而dεij则是以瞬时状态为参考状态计算的，所以d（εij）≠dεij。只有在变形很微小且主应变方向保持不变的情况下，才有d（εij）=dεij。可见，这里dεij中的d表示增量，不是微分的符号，对一般的塑性变形过程，dεij并不表示εij的微分。同理，对dεij的积分一般并不等于εij。

3.应变速率张量

单位时间内的应变称为应变速率，俗称变形速度，用表示，其单位为s-1。

将式（9-77）代入式（9-78a），得

将上式两边除以时间dt，则得应变速率为

或者写成：

一点的应变速率也是一个二阶对称张量，称为应变速率张量。

应注意，是应变增量dεij对时间dt的微商，正如前所述，dεij通常并不是全量应变εij的微分，所以一般也不等于εij对时间的导数，即

应变速率张量与应变增量张量相似，它们都可描述瞬时变形状态。在塑性成形理论中，如果不考虑应变速率对材料性能及外摩擦的影响，或对这种影响另行考虑，则用应变增量和应变速率进行计算所得的结果是一致的。若对于应变速率敏感的材料（如超塑性材料）则需采用应变速率来进行计算。

应变速率张量也有其主方向（主轴方向）、主应变速率）、主切应变速率、应变速率偏张量、应变速率球张量）、应变速率张量不变量、等效应变速率），等等，它们的含义和表达式的形式都和小应变张量一样。

应变速率表示变形的快慢，它不但取决于成形工具的运动速度，而且与变形体的形状尺寸及边界条件有关，所以不能仅仅用工具或质点的运动速度来衡量物体内质点的变形速度。例如，在试验机上均匀压缩一柱体，下垫板不动，上压板以速度下移，取柱体下端为坐标原点，压缩方向为x轴，柱体某瞬时高度为h（如图9-26所示），此时，柱体内各质点在x方向上的速度为

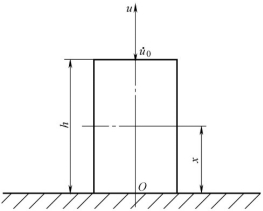
图9-26　单向均匀压缩时的位移速度

于是，各质点在x方向的应变速率分量为

设h=100mm，，则，接近准静态压缩。在锤上锻造时，则；高速锤锻造时=-（15～20）m/s，则。如柱体的高度h压缩为10mm，则上述的应变速率都增加到原来的10倍。显然，位移速度和应变速率是两个不同的概念。