材料力学及一般弹、塑性理论中所讨论的变形常常不超过10-3~10-2数量级,这种很小的变形统称为小变形。
1.小应变
应变可分为正应变与剪(切)应变。设一单元体PABC在xoy坐标平面内发生了微小的变形(见图9-16(a),这里暂不考虑刚体位移),变为PA1B1C1。单元体内各线元长度相应发生变化。若设线元PB由原长r变成了r1=r+δr,则其单位长度的变化为
![]()
称为线元PB的正应变。线元伸长时ε为正,压缩时ε为负。其他线元也可同样定义。例如,平行于x轴和y轴的线元PA和PC,将分别有
![]()
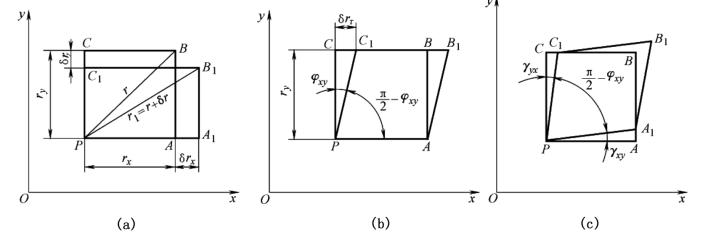
图9-16 单元体在xoy坐标平面内的变形
又设单元体在xoy坐标平面内发生剪(切)变形(见图9-16(b)),线元PA和PC所夹的直角∠CPA缩减了φ角,变成了∠C1PA,相当于C点在垂直于PC的方向偏移了δrτ,一般把
![]()
称为相对切应变,也称工程切应变。∠CPA缩减时φ取正号。图9-16(b)中的φ是在xoy坐标平面内发生的,故可写为φxy。应指出,由于变形很小,故可认为PC偏转至PC1时长度不变。相对切应变可看成PA和PC同时向内偏转相同的角度γxy及γyx(见图9-16(c))。
![]()
γxy、γyx定义为切应变。切应变γij角标的意义是:第一个角标表示线元(棱边)的方向,第二个角标表示线元偏转的方向,如γxy表示x方向的线元向y方向偏转的角度。实际变形中线元PA和PC的偏转角度不一定相同。现设它们的实际偏转角度分别是αxy、αyx(见图9-17(a)),偏转的结果仍然使∠CPA缩减了φxy,于是有
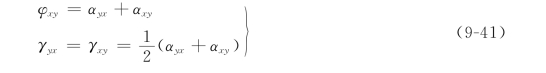
则αxy、αyx中已经包含了刚体转动。假设线元PA和PC先同时偏转了γxy及γyx(见图9-17(b)),然后整个单元体绕z轴转动了一个角度ωz(见图9-17(c)),由几何关系有

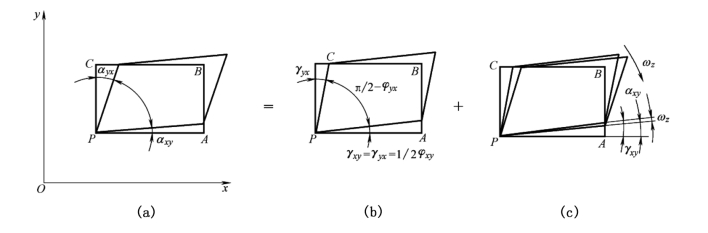
图9-17 切应变与刚性转动
2.点的应变状态和应变张量
在直角坐标系中取一极小的单元体PA…G,边长分别为rx、ry、rz,小变形后移至P1A1…G1,变成了一个偏斜的平行六面体,如图9-18(a)所示。图9-18(b)为它在3个坐标平面上的投影。这时,单元体同时产生正应变、切应变、刚体平移和转动。假设单元体首先平移至P1A'…G',然后可能产生如图9-19所示的3种正应变和3种切应变。
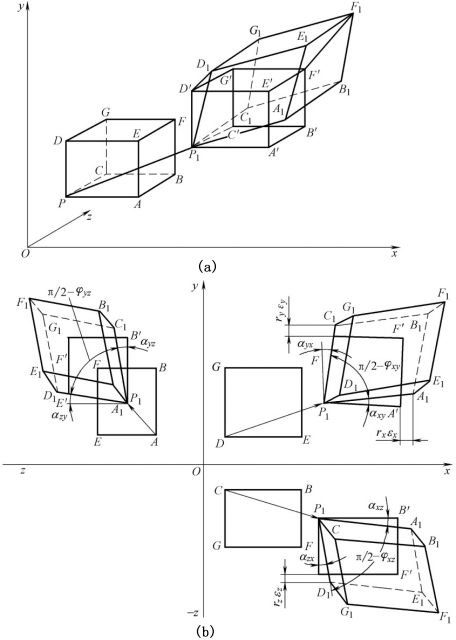
图9-18 单元体变形
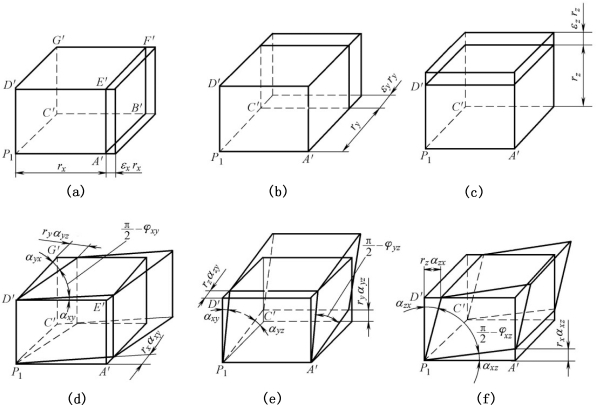
图9-19 单元体变形的分解
(1)单元体在x方向的长度变化了δrx,其正应变为![]() (见图9-19(a))。
(见图9-19(a))。
(2)在y方向的长度变化了δry,其正应变为![]() (见图9-19(b))。
(见图9-19(b))。
(3)在z方向的长度变化了δrz,其正应变为![]() ,(见图9-19(c))。
,(见图9-19(c))。
(4)单元体的P1C'G'D'面(也即x面)在xoy平面中偏转了αyx角,y面(P1A'E'D')偏转了αxy角,形成了工程切应变φxy=αxy+αyx(见图9-19(d))。
(5)y面和z面在yoz平面分别偏转了αzy角αyz,形成了工程切应变φyz=αyz+αzy(见图9-19(e))。
(6)z面和x面在zox平面分别偏转了αxz角αzx,形成了工程切应变φzx=αzx+αxz(见图9-19(f))。
将上述6个变形叠加起来就可得到图9-18(a)中偏斜的六面体P1A1···G1。于是该单元体的变形就可以用上述的εx、εy、εz、φxy、φyz、φzx等6个应变来表示。
3个工程切应变φ由6个偏转角α组成。它们之中实际上包含了切应变与刚体转动,将前述的式(9-40)、(9-41)、(9-42)推广至三维,得到的切应变γij为
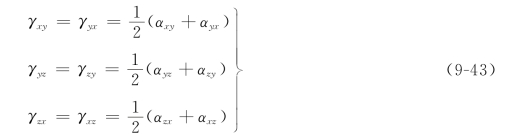
刚体转动为

式中,εx、αxy…等9个分量可构成一个张量,称为相对位移张量rij,而
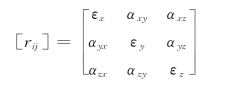
在一般情况下,αxy≠αyx;αyz≠αzy;αzx≠αxz,即rij≠rji,故它是非对称张量的分量。将rij叠加上一个为零的张量的分量(rji-rji)/2,即可把它分解为
![]()
将式(9-43)、(9-44)代入上式,可得
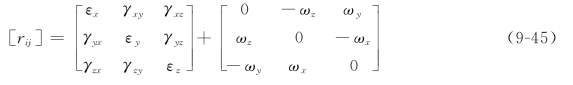
式中的后一项为反对称张量,表示刚体转动,称为刚体转动张量;前一项为对称张量,表示纯变形,这就是我们要重点讨论的应变张量,一般用[εij]表示,即
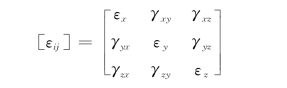
为便于记忆,两个下标的意义可以这样来理解:第一个下标表示通过P点的单元棱边(线元)的方向,第二个下标表示该线元变形的方向。例如,εx(即εxx)表示P点x方向线元在x方向的线应变,γxy表示x方向线元在y方向的偏转角,等等。
进一步观察图9-18(a)可知,当单元体PA…G刚性平移到P1A'…G'时,各角点之间的相对位置都没有发生变化。产生变形后,角点的相对位置才发生变化。其中P1的对顶角点F'移至F1,矢量F'F1就是F点相对于P点的位移,它集中反映了全部变形的结果。因此,只要从位移场出发,分析F点和P点的相对位移,就能建立起变形和位移的关系图。
3.位移分量与小应变几何方程
1)位移及其分量
变形体内一点变形前后的直线距离称为位移。在坐标系中,一点的位移矢量在3个坐标轴上的投影称为该点的位移分量,一般用u、v、w或角标符号ui来表示。
变形体内不同点的位移分量也是不同的。根据连续性假设,位移分量应是坐标的连续函数,而且一般都有连续的二阶偏导数,该函数可表示为

或
![]()
式(9-46)表示变形体内的位移函数,即位移场。
一般情况下,位移场是待求的,而且求解比较复杂。但在某些比较简单而且理想的场合,可以通过几何关系直接求得位移场。例如,图9-47表示一矩形柱体在无摩擦的光滑平板间进行塑性压缩,这时该柱体在压缩后仍是矩形柱体,且可假定其体积不变,如设压缩量δH很小,则柱体内的位移场为
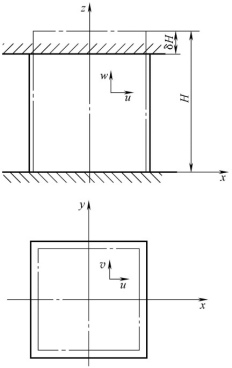
图9-20 光滑平板间镦粗时的位移
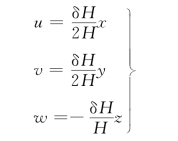
现在来研究变形体内无限接近两点的位移分量之间的关系。设受力物体内任一点M,其坐标为(x,y,z),小变形后移至M1,其位移分量为ui(x,y,z)。与M点无限接近的一点M',其坐标为(x+dx,y+dy,z+dz),小变形后移至![]() ,其位移分量为
,其位移分量为![]() ),如图9-21所示。将函数
),如图9-21所示。将函数![]() 按泰勒级数展开并略去高阶微量,可得
按泰勒级数展开并略去高阶微量,可得
![]()
式中,![]() 称为M'点相对于M点的位移增量。
称为M'点相对于M点的位移增量。
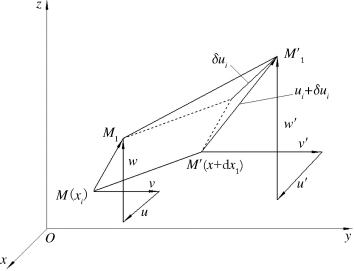
图9-21 变形体内无限接近两点的位移分量及其位移增量
式(9-47)说明,若已知变形物体内一点M的位移分量,则与其邻近一点M'的位移分量可以用M点的位移分量及其增量来表示,其中的位移增量δui可写成
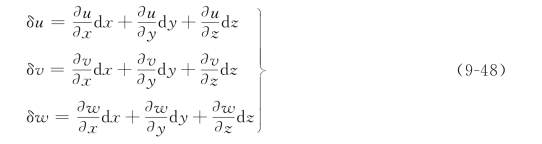
若无限接近两点的连线MM'平行于某坐标轴,如MM'∥x轴,则式(9-48)中的dx≠0,dy=dz=0,此时,式(9-48)变为

2)小应变几何方程
设图9-22中,abdc为单元体变形前在xoy坐标平面上的投影,b、c点为a点的邻近点,并设ac=dx,ac∥ox轴;ab=dy,ab∥oy轴。a1b1d1c1为单元体变形后的投影。设图中a点位移分量为u、v,则b、c点相对于a点的位移增量为
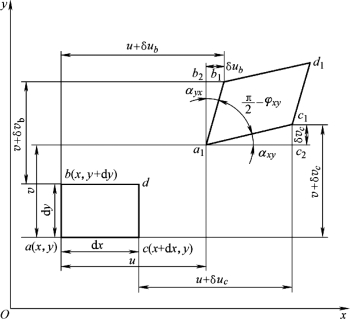
图9-22 位移分量与应变分量的关系

根据式(9-50)和图9-22的几何关系,可求出棱边ac(即dx)在x方向的线应变εx,即
![]()
同理,棱边ab(即dy)在y方向的线应变为
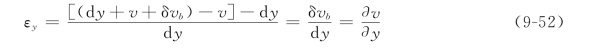
由图9-22的几何关系,有
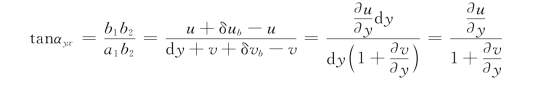
因为![]() ,其值远小于1,故有
,其值远小于1,故有

同理可得
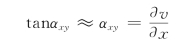
因而工程切应变为
![]()
则切应变为
![]()
类似地,由单元体在yoz和zox平面上投影的几何关系可得其余应变分量的公式。综合上述可得
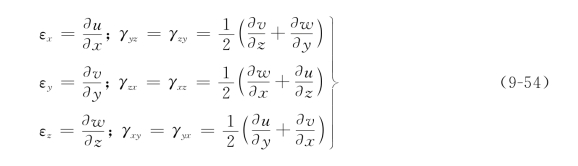
用角标符号表示为

式(9-54)表示小变形时位移分量和应变分量之间的关系,它是由变形几何关系导出的,故称为小应变几何方程。即如果物体中位移场为已知,则由几何方程可求得应变场。
4.应变连续方程
由小应变几何方程可知,6个应变分量取决于3个位移分量。很显然这6个应变分量不应是任意的,其间必存在一定的关系,才能保证变形物体的连续性。应变分量之间的关系称为应变连续方程或应变协调方程,应变连续方程可分为两组,即每个坐标平面内、不同平面间应变分量之间应满足的关系共6个式子。
1)坐标平面内的应变连续方程
在xoy坐标平面内,将几何方程式(9-54)中的εx、εy分别对y、x求两次偏导数,可得

由式(9-55)+式(9-56),得

同理,可得yoz、zox坐标平面内线应变分量与切应变分量的关系式,连同上式综合可得
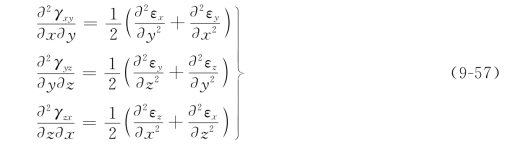
式(9-57)表明,在每个坐标平面内,两个线应变分量一经确定,则对应的切应变分量也就被确定了。(https://www.xing528.com)
2)不同平面间的应变连续方程
将式(13-54)中的εx对y、z,εy对z、x,εz对x、y分别求偏导,并将切应变分量γxy、γyz、γzx分别对z、x、y求偏导数,得
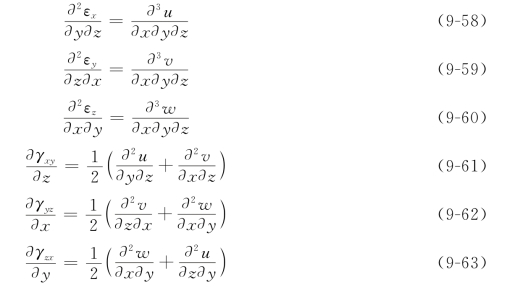
将式(9-61)+式(9-62)-式(9-63),得
![]()
再将上式对y求偏导数,并考虑到式(9-59),得

式(9-64)表明,在不同平面间的3个切应变分量一经确定,则线应变分量也就被确定了。
需要指出的是:如果已知一点的位移分量,并利用几何方程求得应变分量εij,则εij自然满足连续方程。但如果先用其他方法求得应变分量,则只有当它们满足连续方程时,才能用几何方程求得正确的位移分量。
例题9-2 设εx=a(x2-y2);εy=axy;γxy=2bxy。其中a、b为常数。试问上述应变场在什么情况下成立?
解:应变场成立必须满足应变连续方程,根据给定的εx、εy和γxy可求得
![]()
代入连续方程式(9-57)解得
![]()
这说明给定应变场只有在a=-2b时才能成立。
5.塑性变形体积不变条件
由基本假设,塑性变形时物体变形前后的体积保持不变,可用数学式表达。设单元体初始边长为dx、dy、dz,则变形前的体积为
![]()
考虑到小变形时,切应变引起的边长变化及体积变化都是高阶微量,可以忽略,则体积的变化只是由线应变引起的,如图9-23所示。在x方向上的线应变为
![]()
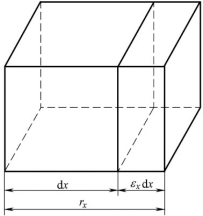
图9-23 单元体边长的线应变
所以
![]()
同理
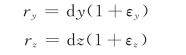
变形后单元体的体积为
![]()
将上式展开,并略去二阶以上的高阶微量,于是得单元体单位体积的变化(单位体积变化率)为
![]()
在塑性变形时,由于材料内部质点连续且致密,体积变化很微小,所以由体积不变假设可得
![]()
式中,εx、εy、εz为塑性变形的3个线应变分量。
式(9-65)称为塑性变形时的体积不变条件。由式(9-65)可以看出,塑性变形时3个线应变分量不可能全部同号,绝对值最大的应变永远和另外两个应变的符号相反。在金属塑性成形过程中,体积不变条件是一项很重要的原则,有些问题可根据几何关系直接利用体积不变条件来求解。
6.点的应变状态表达方式
点的应变张量与应力张量具有相似的形式、性质和特性。在研究点的应变状态时一些公式不需再推导,可直接由与应力张量相似性得到,只需将应变张量中的线应变分量和切应变分量分别与应力张量中的正应力分量和切应力分量相对应即可。
1)主应变、应变张量不变量、主切应变和最大切应变、主应变简图
(1)主应变。变形体内一点存在有3个相互垂直的应变主方向(也称应变主轴),该方向上的线元没有切应变,只有线应变,称为主应变,用ε1、ε2、ε3表示。
若取应变主轴为坐标轴,则应变张量为

(2)应变张量不变量。若已知一点的应变张量,求过该点的3个主应变,也存在一个应变状态的特征方程:
![]()
对于一个确定的应变状态,3个主应变具有单值性,故上述特征方程式中的系数I1、I2、I3也应具有单值性,即它们都是应变张量的不变量,其表达式为
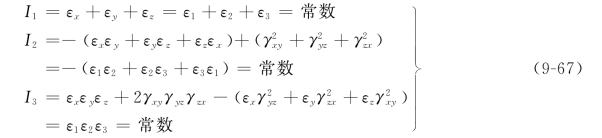
(3)主切应变和最大切应变。在与应变主方向成±45°角的方向上存在3对各自相互垂直的线元,它们的切应变有极值,称为主切应变。主切应变的计算公式为
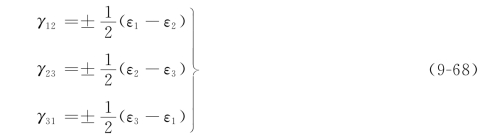
3对主切应变中,绝对值最大的主切应变称为最大切应变。若ε1≥ε2≥ε3,则最大切应变为
![]()
(4)主应变简图。用主应变的个数和符号来表示应变状态的简图称为主应变状态图,简称主应变简图或主应变图。3个主应变中绝对值最大的主应变反映了变形的特征,称为特征应变。由塑性变形的体积不变条件可知,特征应变等于其他两个应变之和,但方向相反。如用主应变简图来表示应变状态,根据体积不变条件和特征应变,则塑性变形只能有如下3种变形类型,如图9-24所示。
①压缩类变形:如图9-24(a)所示,特征应变为负应变(即ε1<0),另两个应变为正应变,即-ε1=ε2+ε3。
②剪切类变形(平面变形):如图9-24(b)所示,一个应变为零,其他两个应变大小相等,方向相反,即ε2=0,ε1=-ε3。
③伸长类变形:如图9-24(c)所示,特征应变为正应变(即ε1>0),另两个应变为负应变,即ε1=-(ε2+ε3)。
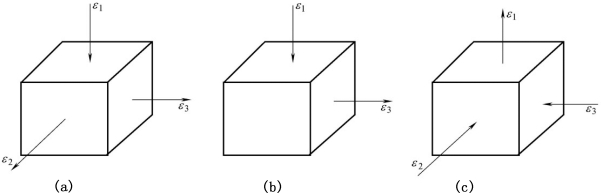
图9-24 3种变形类型
主应变简图对于分析塑性变形时金属流动具有重要意义,它可以用来判定塑性变形的类型。
2)应变偏张量和应变球张量
应变张量也可以分解为如下两个张量,即
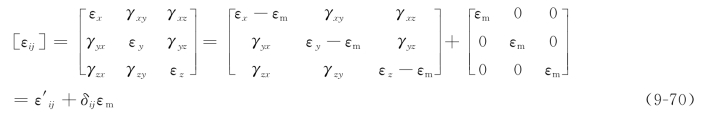
式中,![]() ,称为平均应变;
,称为平均应变;![]() 称为应变偏张量,表示变形单元体形状的变化;δijεm称为应变球张量,表示变形单元体体积的变化。
称为应变偏张量,表示变形单元体形状的变化;δijεm称为应变球张量,表示变形单元体体积的变化。
应变偏张量也有3个不变量,称为应变偏张量的第一、第二和第三不变量:
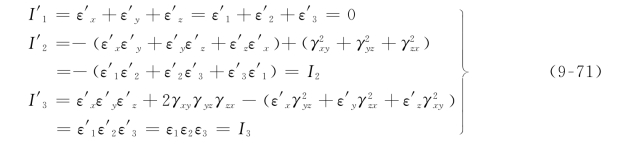
塑性变形时,根据体积不变条件,有εm=0,故此时应变偏张量即为应变张量。
3)八面体应变
如以3个应变主轴为坐标轴,同样可作出正八面体,八面体平面的法线方向线元的应变称为八面体应变,分为八面体线应变和八面体切应变,分别记为ε8、γ8。
八面体线应变为
![]()
八面体切应变γ8为
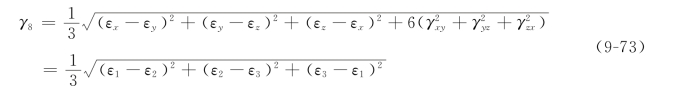
4)等效应变
取八面体切应变绝对值的![]() 倍所得之参量称为等效应变,也称广义应变或应变强度,记为
倍所得之参量称为等效应变,也称广义应变或应变强度,记为
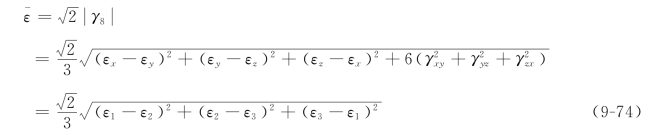
按照与应力分析中类似的方法可以推得等效应变的形式更简单的表达式:

等效应变有如下特点:
(1)等效应变是一个不变量。
(2)在塑性变形时,等效应变在数值上等于单向均匀拉伸或均匀压缩方向上的线应变ε1,即 =ε1。因单向应力状态时,其主应变为ε1,ε2=ε3,由体积不变条件可得
=ε1。因单向应力状态时,其主应变为ε1,ε2=ε3,由体积不变条件可得![]() ,代入式(9-74),得
,代入式(9-74),得
![]()
(3)等效应变并不代表某一实际线元上的应变,因此在坐标系中不存在这一特定线元。
(4)等效应变可以理解为代表一点应变状态中应变偏张量的综合作用。
例3设一物体在变形过程中某一极短的时间内的位移场为
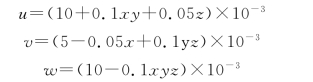
试求点A(1,1,1)的应变分量、应变球张量、应变偏张量、主应变、等效应变与最大剪应变。
解:根据小变形几何方程式(9-54),可得
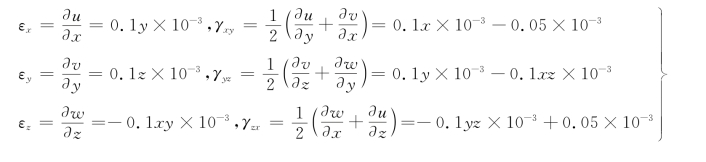
将P点坐标x=1,y=1,z=1代入上述各式,得P点的应变张量为

因![]() ,则该点的应变球张量、应变偏张量分别为
,则该点的应变球张量、应变偏张量分别为
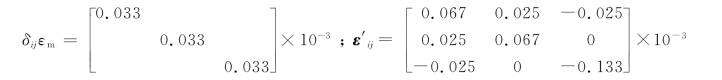
根据式(9-67)得3个应变不变量为

代入应变张量特征方程,得
![]()
令104·ε=t,方程变为
![]()
解方程得3个根为t1=1.264,t2=0.767,t3=-1.031,则3个主应变为
![]()
由式(9-74)得等效应变为
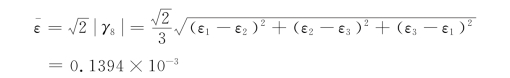
由式(9-69)得最大剪应变为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




