探究特殊应力状态的影响和表现

利用解析方法求解一般的三向应力状态问题是很困难的。某些特殊问题，如部分简单冲压工艺、镦粗工艺等可近似地简化为特殊应力状态，从而使得应力张量和平衡微分方程可以得到某些简化，有可能找到相应的解析解。

1.平面应力状态

平面应力状态的基本特征如下述。

①物体内所有质点在与某一方向垂直的平面上都没有应力，如取该方向为坐标的z轴，则有σz=τzx=τzy=0，只留下σx、σy、τxy这3个应力分量。z向必为主方向，所有质点都是两向应力状态；②各应力分量都与z坐标无关，因此整个物体的应力分布可以在xy坐标平面上表示出来。材料力学中的一些问题，如梁的弯曲、薄壁管扭转等都是平面应力状态。另外，薄壁容器承受内压以及塑性成形中的一些板料成形工序，例如拉深工艺等，由于壁厚或板厚方向的应力相对很小，可以忽略，所以一般也看成是平面应力状态。根据上述分析，平面应力状态的应力张量为

或

在两向应力状态中有一种“纯剪”状态，它的特点是在主剪平面上的正应力为零，如图9-12（a）所示。棒料或者管料在小变形扭转时就是这种状态。纯剪状态的应力莫尔圆如图9-15（b））所示，纯剪应力τ就是最大剪应力，主轴与坐标轴成45°角，主应力的特点是σ1=-σ2=τ。

图9-12　纯剪应力状态及其莫尔圆

平面应力状态时，由于σz=τzx=τzy=0，所以其平衡微分方程为

2.轴对称应力状态

回转体所受外力对称于回转轴且没有周向力时，则物体内的质点就处于轴对称应力状态。处于轴对称状态时，回转体的每个子午面都始终保持平面，而且各子午面之间的夹角始终不变。用圆柱坐标表示的单元体及应力状态如图9-13所示，其一般的应力张量为(www.xing528.com)

图9-13　圆柱坐标中单元体上的应力分量

平衡微分方程的一般形式为

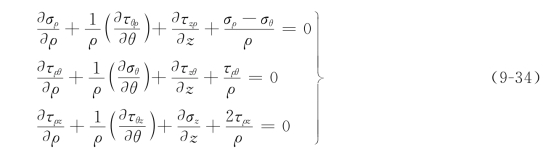
轴对称状态时，由于子午面（也即θ面）在变形过程中始终不会扭曲，所以其特点是：①在θ面上没有剪应力，即τρθ=τθz=0，故应力张量只有σρ、σθ、σz、τρz这4个分量，而且σθ是一个主应力；②各应力分量与θ坐标无关，对θ的偏导数都为零。所以，用圆柱坐标时的平衡微分方程为

用球坐标时的单元体及应力状态如图9-14所示，其应力分量为σρ、σθ、σφ、τρθ、τθφ、τφρ。一般的平衡微分方程为

轴对称状态时，τθρ=τθφ=0，各分量对θ的偏导数为零，故用球坐标时其平衡微分方程为

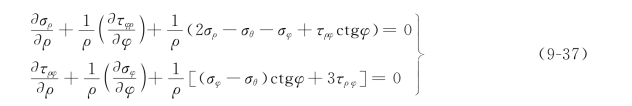
图9-14　球坐标中单元体上的应力分量