应力张量及其主要特性

由前面的论述可知，当物体受到一个外力作用时，其内部任意质点的应力状态是确定的。但是，随着坐标系的变化，应力分量将相应变化。由此可知，不同坐标系的应力分量之间必然存在一定的关系。若设图9-4中斜截面法线N是某一坐标系ox'y'z'的一个坐标轴，如x'轴，则式（9-7）所示的σ为新坐标系中的，N的方向余弦l、m、n就是新坐标轴x'在原坐标系中的方向余弦，改写为lx'x、lx'y、lx'z，简记为lx'i（i=x，y，z）。式（9-5a）可改写为

式（9-6）也可写成

将上式按求和约定展开，并考虑到i=j时，lx'i=ljx'，即可得到式（9-7）。在式（9-8）中的剪应力τ没有按坐标方向分成两个分量，但如给出新坐标系另两个坐标轴y'、z'在原坐标系中的方向余弦ly'i及lz'i，那么把Sj分别投影到y'及z'轴上，也即分别乘以ljy'及ljz'，即可直接求得x'微分面上的两个剪应力分量：

将（9-10）、（9-11）、（9-12）三式合并表示如下：

对y'及z'方向的微分面上的应力进行类似处理，得到

式（9-13）即为该应力状态在ox'y'z'坐标系中的9个分量，可通过原坐标系oxyz中的应力分量σij及x'、y'、z'轴的方向余弦求得。不同坐标系中的9个量可以用式（9-13）所示的线性关系来变换，则此9个量就构成一个特殊的物理量，叫做二阶张量，简称张量（参看附录B）。因此，一点的应力状态是张量，叫做应力张量。式（9-4）所示的矩阵叫张量矩阵。由剪应力互等、张量矩阵主对角线两边对称，得到应力张量为二阶对称张量，可表示为

应力张量具有张量的许多特性，如可以合并、分解，存在主方向、主值及不变量等等，它们对于分析应力状态很有用，同时对于判断材料成形性能优劣、制定合理成形工艺具有重要作用。应力张量的主应力及不变量、应力球张量、应力偏张量、主剪应力及最大剪应力、八面体应力和等效应力在塑性成形中具有重要意义，下面将分别展开论述。

1.主应力和应力不变量

根据式（9-7）及式（9-8），若一点应力状态确定，则有可能存在一组特殊的法线方向，使剪应力τ≡0。另外，由张量的性质可知，一个二阶对称张量必然有3个相互垂直的方向，叫做主方向。在主方向上，下标不同（i≠j）的分量均为零，此时下标相同（i=j）的分量叫做该张量的主值。对于应力张量，主值就是主方向上的3个正应力，叫做主应力；与3个主方向垂直的微分面叫主平面，主平面上剪应力为零；与3个主方向一致的坐标轴称为主轴。具体证明见附录B或相关张量专著。利用线性代数方法也可证明上述结论。

设图9-4中的法线方向余弦为l、m、n的斜截微分面ABC为主平面，面上的剪应力τ=0，由式（9-8）可得主应力σ=S，其在3个坐标轴方向上的投影相应为Sx、Sy及Sz，即

将S的分量代入式（9-5），整理得到以l、m、n为未知数的齐次线性方程组：

其解就是应力主轴的方向。此方程组的一组解是l=m=n=0。由解析几何可知，方向余弦之间必须满足

它们不能同时为零，因此必存在非零解。方程组（9-14）存在非零解的条件是方程组的系数所组成的行列式等于零，即

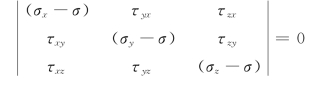
展开整理后得

设

则上式可写成

式（9-17）为一个以σ为未知数的三次方程，叫做应力状态的特征方程，方程必然有3个实根（证明见附录B），即3个主应力，用σ1、σ2、σ3表示。将解得的主应力代入式（9-14）并与式（9-15）联解，即可得到该主应力的方向余弦，即3个相互垂直的主方向。

对于一个确定的应力状态，只能有一组（3个）主应力的数值。因此，特征方程式（9-17）的系数J1、J2及J3是单值的，不随坐标而变。由此得出重要结论：尽管应力张量的各分量随坐标而变，但按式（9-16）组合起来的函数的值是不变的。因此，J1、J2及J3分别称为应力张量的第一、第二和第三不变量。存在不变量也是张量的特性之一。应力张量的这3个不变量在塑性加工中具有重要物理意义。

如果取三个主方向为坐标轴，则通常用下标1、2、3代替x、y、z，这时应力张量写为

将式（9-4a）的各分量代入式（9-7）、（9-8），即可得到主轴坐标系中斜截面上的正应力和剪应力公式：

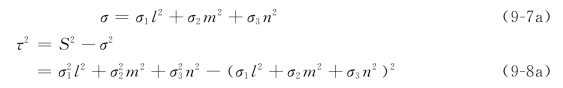
此时3个应力不变量为

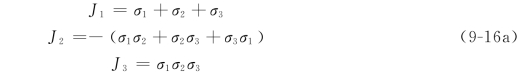
点的应力状态还可在主轴坐标系中用几何图形进行表示。将主轴坐标系的应力分量式（9-4a）代入式（9-5），得到任意斜截面上全应力的3个分量S1、S2及S3：

或

考虑到

得

对于一点的应力状态，主应力σ1、σ2、σ3是确定的，则（9-18）表示一个椭球面，叫做应力椭球面，它表示过一点的任意截面上全应力矢量S端点的轨迹（见图9-5），其主半轴的长度分别等于σ1、σ2、σ3。还可发现，3个主应力中的最大值和最小值即该点所有方向的应力中的最大值和最小值。

图9-5　应力椭球面

主应力的特点可以用于对成形过程中材料的应力状态进行区分：σ1，σ2，σ3≠0，称为三向应力状态，见图9-6（a）。此种应力状态常见于锻造、挤压、轧制等工艺；若3个主应力中有一个为零，则称为二向应力状态，见图9-6（b）。此时，应力椭球面退化为在某个平面上的椭圆轨迹。此种应力状态存在于弯曲、扭转等工艺中；若3个主应力中有两个相等，如σ1≠σ2=σ3，则可称为圆柱形应力状态，见图9-6（c）。此处“圆柱形”表示应力分布的特点，而不是应力椭球面的退化形状。单向应力状态时σ1≠σ2=σ3=0，也属于这种状态。在这种状态下，与σ1轴垂直的所有方向都是主方向，且这些方向上的主应力都相等；若3个主应力相等，则椭球面变为球面（见图9-6（d）），称为球应力状态。由式（9-8a）可知，此时τ≡0，即所有方向都没有剪应力，均为主方向，且所有方向的应力相等。

图9-6　各种应力状态

利用主应力表示应力张量可使运算大为简化。同时，塑性成形中质点主应力还被用来衡量变形金属工艺塑性的优劣。

例题9-1 设某点的应力状态如图9-7（a）所示，试求其主应力及主方向（应力单位：N/mm2）。

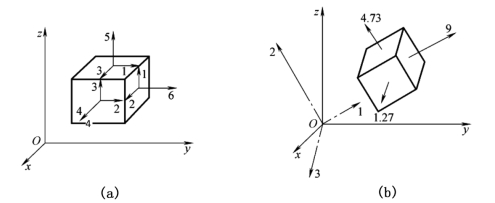
图9-7　某点应力状态、主应力和主方向

解 图9-7（a）所示的应力张量为

代入式（9-16），得

代入（9-17），得

解得

将应力分量代入式（9-14），并与式（9-15）联立，得

将解得的3个主应力值分别代入上式，并联解方程组（注：上列方程组中的前三式是不定方程组，可用其中两式与第四式联解，或者求出不定方程的通解代入第四式求解），得到的3个主方向的方向余弦为

所得主应力及主方向如图9-7（b）所示。

2.主剪应力和最大剪应力

金属塑性变形的一个重要指标是材料所受的剪应力。由前可知，主应力的方向对应正应力的极值。类似地，斜截面上的剪应力也必然存在极值，此极值称为“主剪应力”。主剪应力所在平面称为“主剪应力平面”。取3个主应力方向构成参考坐标系，则任意斜截面上的剪应力可由式（9-8a）确定：

(www.xing528.com)

考虑到3个方向余弦值不独立，将n2=1-l2-m2代入上式消去n得

对式（9-19）求极值，即分别对l、m求偏导并使之等于零，得

显然l=m=0是式（9-20）的一组解，则n=±1，为一对主平面，剪应力为零。此组解不是要找的解。当σ1=σ2=σ3，即球处于应力状态时，τ≡0，上式无解。如σ1≠σ2=σ3，则从第一式解得，圆柱处于应力状态。此时与σ1轴成45°（或135°）的所有平面都是主剪应力平面，单向拉伸就是如此。对于σ1≠σ2≠σ3的一般情况，如l≠0，m≠0，则式（9-20）中两式的方括号内的项必同时为零，因此将有σ1=σ2，与前提条件σ1≠σ2≠σ3不符，因此这种情况下式（9-20）无解。如l=0，m≠0，即斜截微分面始终平行于1轴（参见图9-8（a）），则由式（9-20）的第二式得

图9-8　主剪应力平面

由此解得

l=0，，从而。若l≠0，m=0，则可由式（9-20）第一式解得

如最初从式（9-8a）消去l或m，可同样求解。除去重复的解，还可以得到一组解为

上述3组解各表示一对相互垂直的主剪应力平面，它们分别与一个主平面垂直并与另两个主平面成45°角，如图9-8（b）所示。每对主剪应力平面上的主剪应力都相等。将上列3组方向余弦值代入式（9-8a），即可求得3个主剪应力如下：

主剪应力中绝对值最大的一个，即一点所有方向截面上的最大剪应力，叫做最大剪应力，以τmax表示。如设σ1≥σ2≥σ3，则

将3组方向余弦值代入式（9-7a），即可求得主剪应力平面上的正应力为

应注意到，每对主剪应力平面上的正应力都是相等的，图9-9所示为σ1σ2平面上的例子。

图9-9　主剪应力平面上的正应力

下面将6对特殊平面的结果列于表9-1中。

表9-1　6对特殊平面的方向余弦和应力

3.应力球张量和应力偏张量

与矢量类似，应力张量是可以分解的。设σm为3个正应力分量的平均值，即

σm叫做平均应力，是不变量，与坐标系无关。对于一个确定的应力状态，它是单值的。

3个正应力分量可表示为

将上式代入应力张量式（9-4），即可将应力张量分解成两个张量：

用张量的分量符号可简记为

其中，δij叫克氏符号（Kronecker delta），是单位球张量的标记，详见附录A。

张量的分量δijσm表示球应力状态，故称应力球张量。在球应力状态下，任何方向都是主方向，而且主应力相同，所以σm可看成是一种静水应力。另外，由于球应力状态在任何截面上都没有剪应力，所以它不能使物体产生形状变化和塑性变形，只能产生体积变化。

叫做应力偏张量，它是由原应力张量减去球张量后得到的，其分量表示为

由于应力球张量没有剪应力，任意方向都是主方向且主应力相同，因此，减去球张量后得到的的剪应力分量、主剪应力、最大剪应力及应力主轴等等都与原应力张量相同。应力偏张量只能使物体产生形状变化，而不能产生体积变化。应力偏张量同样有3个不变量，可用及表示。将应力偏张量的分量代入式（9-16），可得

对于主轴坐标系，则

将式（9-26）中的第一式两边平方后整理可得

将上式代入式（9-26），第二式可得

4.八面体应力和等效应力

设物体内任意点Q为原点，以该点的应力主轴为坐标轴，在无限靠近Q点处作等倾微分面，其法线与三根坐标轴的夹角都相等，即。坐标空间8个象限的等倾斜微分面可以形成一个正八面体（见图9-10）。这种微分面叫八面体平面，面上的应力叫八面体应力。

图9-10　八面体和八面体平面

八面体平面的方向余弦为

将上述方向余弦代入斜截面应力公式（9-7a），得八面体正应力为

将八面体平面的方向余弦代入式（9-8a），整理后得八面体剪应力为

可见，σ8就是平均应力或静水应力，是不变量。τ8则是与应力球张量无关的不变量。对于一个确定的应力偏张量，τ8是确定的。上述两式中的J1和分别用式（9-16）和（9-26）中的函数式代入，即可得到任意坐标系中的应力分量表示的八面体应力：

进一步地，将八面体剪应力τ8取绝对值，并乘以系数，所得到的量仍是一个不变量，称为“等效应力”，也称广义应力或应力强度，在本书中以¯σ表示。对于主轴坐标系，等效应力的表达式为

对于任意坐标系，则为

将式（9-26b）代入式（9-29）得

前面讨论的主应力、主剪应力、八面体应力等都是在某些特殊微分面上实际存在的应力，而等效应力则是不能在某特定微分面上表示出来的。但是，等效应力可以在一定意义上“代表”整个应力状态中的偏张量部分，因此，它和塑性变形的关系非常密切，在金属塑性成形中具有十分重要的意义。

具体地，根据式（9-29），单向应力状态下

三向应力状态下如σ1≥σ2≥σ3，则有

可见，和最大剪应力的2倍相差不大。