最简单易懂的应力状态解析

由前述可知，一点的应力状态无法用某一方向截面上的应力来完整描述。假设直角坐标系中一承受任意外力的物体处于静力平衡状态，在物体内任一点Q取一微小的六面体单元，该六面体的所有面分别平行于3个坐标平面。取六面体中3个相互垂直的表面作为微分面，若此3个微分面上的应力已知，则根据空间物体的静力平衡条件，该单元体任意方向上的应力都可确定，即在直角坐标系中可以用3个相互垂直的微分面上的应力来完整描述该质点的应力状态。相应地，3个微分面上的应力均可沿坐标轴方向分解为3个分量。考虑到每个微分面都平行于一个坐标平面，因此分解后必有一个应力分量为垂直于微分面的正应力分量，两个为平行于微分面的剪应力分量，3个微分面共有9个应力分量。因此，一点的应力状态通常可用9个应力分量来描述，如图9-3所示。

为了明确表示各微分面上的应力分量，微分面可用各自的法线方向命名，如图9-3中ABCD面叫x面，CDEF面叫y面等。每个应力分量通过两个下标进行标识，本书中约定，第一个下标表示应力分量的作用面，第二个下标表示作用方向。依此规则，两个下标相同的是正应力分量，如σxx表示x面上平行于x轴的正应力分量，可简写为σx；两个下标不同的是剪应力分量，如τxy表示x面上平行于y轴的剪应力分量。9个应力分量可表示如下：

图9-3　单元体上的应力分量

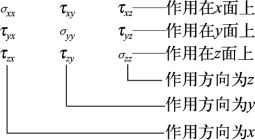
应力分量的正、负号本书中约定按如下方法确定：在单元体上，外法线指向坐标轴正向的微分面（图9-3中的前、右、上3个面）称为正面，反之称为负面；在正面上，指向坐标轴正向的应力分量取正号，指向负向的取负号。负面上的应力分量则相反，指向坐标轴负向的为正，反之为负。按此规定，正应力分量以拉为正，以压为负，图9-3中画出的剪应力分量都是正的。同时，考虑到单元体处于静力平衡状态，则单元体沿3个坐标轴方向的合力矩为零，由此可得到如下关系：

式（9-3）称为剪应力互等定律。它表明剪应力总是成对出现的。因此，一点的应力状态只需用6个独立的应力分量即可表示。

另外，一点应力状态还可以用符号σij（i，j=x、y、z）表示9个应力分量，下标i、j分别依次等于x、y、z，即可得到应力的9个分量，如i=x、j=x可得σxx，即σx；如i=x、j=y则得σxy，即τxy。也可以矩阵形式表示为

“σij”形式的符号叫带下标符号的应力张量，它可使书写大为简化，详见附录A。

上述应力状态表示中各应力分量的描述是基于直角坐标系的，实际塑性成形问题中还经常用特殊坐标系如柱坐标系、球坐标系及更为复杂的曲线坐标系中的应力状态来描述，相关论述可参考本章的后续内容及相关书籍。

由前述分析可知，如果一点的所有应力分量已知，则可通过静力平衡条件求得该点任意方向上的应力。在直角坐标系中任取一质点Q，设其应力分量为σij，若任意方向的斜截面ABC将Q点处的单元体切为一个四面体QABC（见图9-4），则ABC面上的应力就是质点在任意截面上的应力，可由四面体QABC的静力平衡条件确定。若设ABC面的法线为Ν，则其方向余弦为l、m、n（或lx，ly，lz）。

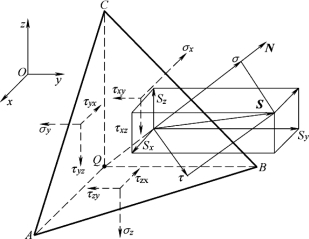
图9-4　斜截微分面上的应力

简写为

设ABC的面积为dA，QBC（x面）、QCA（y面）、QAB（z面）的面积分别为dAx、dAy及dAz，则

(www.xing528.com)

设ABC面上的全应力为S，其3个坐标轴方向的分量为Sx、Sy、Sz。由3个坐标轴方向的静力平衡条件得

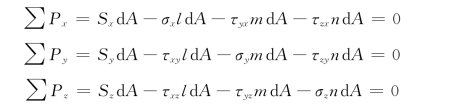
整理后可得Sx、Sy、Sz的表达式为

经整理简写为

这里下标i，j=x，y，z。式（9-5a）按附录A中的下标求和约定进行简写。

斜截微分面ABC上的全应力S可由下式确定：

进而斜截微分面上的正应力和剪应力也可确定。正应力σ就是S在法线N上的投影，即

将式（9-5）代入式（9-6），并考虑到τij=τji，整理后可得正应力为

由

可得斜截微分面上的剪应力为

如果质点处在物体的边界上，斜截微分面ABC为物体的外表面，设该面上作用的外力为Tj（j=x，y，z），则由静力平衡条件可知式（9-5）仍成立。用Tj代替式（9-5a）中的Sj，得到

上式即为应力边界条件表达式。