正弦交流电路基本知识模块4

一、交流电

所谓交流电,是指大小和方向都随时间作周期性变化的电流(或电动势、电压)。我们日常生活或生产中用的交流电是随时间按正弦规律交变的,所以称为正弦交流电,简称交流。

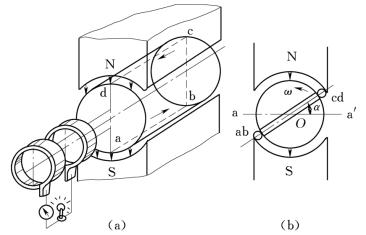
图1-19　交流发电机原理示意图

(a)透视图;(b)剖面图

注意:交流电的大小和方向都在变化,如果只有大小变化,而方向没有变化的不是交流电,而是直流电。例如:电池供电的电流、电压随时间的增加,电流逐渐减小,电压逐渐降低。

二、正弦交流电动势的产生

图1-19所示为一台交流发电机工作原理示意图。一对固定于机壳上的磁极,磁极间有一个可以自由转动的电枢,电枢上绕着绕组,绕组两端分别接在两个彼此绝缘的铜环上,铜环上装有电刷,通过铜环和电刷使绕组和外电路的负荷连接。

当磁场中的绕组被原动机带动转动时,绕组中产生了感应电动势。该电动势产生的电流通过灯泡和检流计构成了闭合电路,使外电路中的灯泡发光,检流计的指针摆动。

由前述导线切割磁力线产生感应电动势的原理可知,当L和v一定时,感应电动势的大小取决于B的大小。为了得到随时间按正弦规律变化的交流电动势,在制造发电机时将磁极做成一定的形状,使磁通密度沿着电枢表面垂直方向按正弦规律分布,即

式中 Bm——磁通密度的最大值,T;

α——绕组的一边与转轴O所组成的平面与中性面(两磁极间的分界面)间的夹角。

所以,感应电动势也是空间角α的正弦函数,即

式中 Em——感应电动势的最大值,V。

当绕组单位时间内旋转的角度(又称角速度)为ω时,空间角α=ωt,则感应电动势e随时间变化的规律可写成

式中 ωt——电动势在时间为t时的角度,称为电动势的相位角。

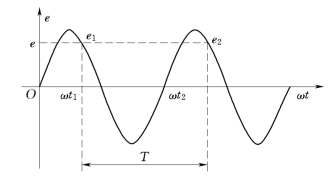
图1-20　正弦交流电的周期

三、周期和频率

正弦交流电随时间按正弦规律由正到负、由负到正周而复始地变化。变化一周所需要的时间称为周期,单位为s,符号用T表示,如图1-20所示。以电角度表示的一个周期为2π弧度,即

每秒正弦量交变的次数称为频率,单位为Hz(赫兹),用f表示。我国电网采用的频率是50Hz。周期和频率互为倒数,即

因为一个周期(360°)等于2π弧度,若将频率的单位Hz化为rad/s(弧度每秒),即为角频率ω,因此

【例1-5】 频率为50Hz的交流电,问它的周期和角频率各是多少?

解:　

ω=2πf=2×3.14×50=314(rad/s)

四、瞬时值与最大值

(1)瞬时值。交流电任一时刻的数值称为瞬时值。用英文小写字母表示。如电流用i、电压用u、电动势用e等。

(2)最大值。正弦交流电瞬时值中的最大值。用有下标m的英文大写字母表示。如交流电流、电压、电动势的最大值分别用Im、Um、Em表示。对于给定的正弦交流电的最大值是常数,在一个周期内出现两次,即正最大值和负最大值。

五、有效值

交流电的瞬时值是随时间变化的,用瞬时值来反应交流电在电路中产生的效果很不方便。同时,用最大值也不能确切地反映出交流电的大小。工程中常用有效值。

如果一个交变电流通过一个电阻,在一周期的时间内所产生的热量和某一直流电流通过同一电阻,在相等的时间内所产生的热量相等,则此直流值就定义为该交流电的有效值。即交变电流的有效值等于与它热效应相当的直流值。

交流电的有效值用英文大写字母表示,如用U、I、E分别表示电压、电流、电动势的有效值。

正弦交流电的有效值等于最大值的即0.707倍,或者说正弦交流电的最大值等于有效值的,即近似为1.414倍。即

在工程计算与实际应用中,电流、电压和电动势的数值通常指有效值。

【例1-6】 用伏特表测得电源电压为220V,问这个电压的最大值为多少?

解:　

六、相位、初相位和相位差

(一)相位、初相位

在交流发电机中,当电枢绕组平面的起始位置与中性面a-a'重合时,感应电动势瞬时值的表达式为(www.xing528.com)

e=Emsinα=Emsinωt　(1-28)

如果以电枢绕组平面在与中性面夹角为φ时作起始位置(即t=0时,α=φ),如图1-21所示。经过t(s)后,电枢绕组平面与中性面的夹角增加了ωt,因此绕组所处位置的角度为α=ωt+φ,则绕组中感应电动势的瞬时值应为

e=Emsin(ωt+φ)　(1-29)

式中 ωt+φ——相位角或相位。

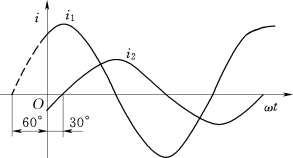
图1-21　电动势的相位和初相位

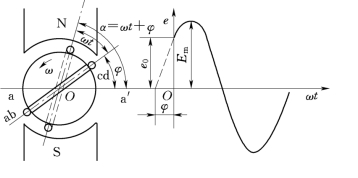
图1-22　初相位的正负值

相位是随时间变化的,它决定了正弦电动势瞬时值的大小和方向。t=0时的相位角φ,称为初相位角或初相位。在波形图上,初相位φ是正弦曲线正向过零点与坐标原点之间的角度。如正向过零点在纵轴左侧时,初相位是正值;在右侧时,初相位是负值。如图1-22中电流i1的初相位为+60°,电流i2的初相位为-30°,它们的瞬时值表达式分别为

(二)相位差

两个完全相同的电枢绕组,它们在电枢上的空间位置如图1-23(a)所示。由于它们绕在同一电枢上,所以两个绕组以同一角速度切割磁力线,它们产生的感应电动势分别为

这两个电动势的最大值和角频率相同,只是相位不同。两个同频率的正弦量在相位上的差别称为相位差,即

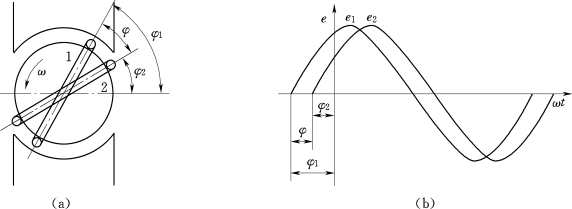
图1-23　相位差

(a)两绕组的空间位置;(b)电动势波形图

由图1-23(b)看出,由于e1和e2存在相位差,所以在同一时刻它们的瞬时值不相等,且e1总比e2先到达最大值,就是说e1在相位上超前e2为φ角,或者说e2较e1滞后φ角。

在图1-22中,i1和i2间的相位差为

φ1-φ2=60°-(-30°)=90°

就是说i1超前i290°,或者说i2滞后i190°。

如果两个同频率的正弦量的相位差为零,这两个正弦量为同相位;如果相位差为180°,则这两个正弦量为反相位。

七、正弦交流电的表示方法

正弦交流电一般有三种表示方法:解析法、曲线法、相量图法。一个正弦量的相量图,波形图,解析式是正弦量的几种不同表示方法,它们是一一对应的关系。

(一)解析法

利用正弦函数表达式形式表示正弦交流电的方法,也可称瞬时值表示法。

(二)曲线法

在平面直角坐标系中作出曲线的方法叫做曲线法,也称波形图法。横坐标表示电角度,或者时间,纵坐标表示电压(或电流,或电动势)大小。

作波形图一般采用五点作图法,如图1-24为函数u=100sin(100πt-π/6)的波形图。

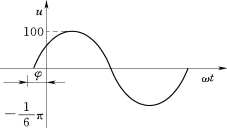
图1-24　函数波形图

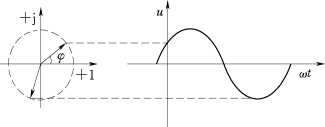
图1-25　振幅相量表示法

(三)相量图法

如果要对正弦交流电进行加,减运算,无论是运用波形图还是解析式表达式,都不是很方便。为此,引入正弦交流电的相量图表示法。

用一个在直角坐标中绕圆点作逆时钟方向不断旋转的矢量来表示正弦交流电的方法称为旋转矢量法,也称为相量图法。正弦量可以用振幅相量或有效值相量表示。振幅相量表示法:用正弦量的振幅值作为相量的模(大小),用初相角作为相量的幅角,如图1-25所示。

图1-26　有效值相量表示法

有效值相量表示法:用正弦量的有效值作为相量的模(长度大小),仍用初相角作为相量的幅角。例如,函数u=50sin(100πt+45°)的有效值相量表示法如图1-26所示。

应用相量图时注意以下几点。

(1)同一相量图中,各正弦交流电的频率应相同。

(2)同一相量图中,相同单位的相量应按相同比例画出。

一般取直角坐标轴的水平正方向为参考方向,逆时针转动的角度为正,反之为负。有时为了方便起见,也可在几个相量中任选其一作为参考相量,并省略直角坐标轴。

正弦交流电用相量表示后,它们的加,减运算可按平行四边形法则进行。