改进型混合蛙跳算法：MSFLA的优化

在SFLA中，在模因组子群内部迭代计算时，对Fw位置的调整和更新是算法核心环节。随着迭代次数增加，子群内个体青蛙位置的更新过多依赖于Fb而弱化了Fg，这样会导致趋同性，进而减少种群的多样性。同时，SFLA容易陷入局部最优解和求解精度低的缺陷。针对这些问题，本书提出了一种改进型SFLA算法（Modified Shuffled Frog-Leaping Algorithm，简称MSFLA）。该算法针对SFLA算法的不足，在两个方面进行了改进。第一，MSFLA改进了Fw位置更新策略；第二，用高斯变异随机扰动替代SFLA中随机产生新解，避免了SFLA盲目搜索的不足。MSFLA具有平衡全局与局部搜寻以及提高分类的求解精度能力。

1.Fw更新策略

在SFLA算法中，在产生一个Fnew_w之前会先将同一子群中Fb和Fw进行比较。如果Fnew_w＜Fb，再将Fg和Fw进行比较产生一个Fnew_w.不难看出，Fw更新过程中Fb的作用比Fg比大。这样容易使Fnew_w收敛于局部最优解。基于Fw更新公式（6-54）和（6-55），本书提出了一种新的Fw更新策略。

设Uz_c是第z组模因子群的中心点，则该中心点如式（6-56）：

式中　P——表示第z组中青蛙的数量；

d——表示维数。

设整个种群中位置最好的青蛙Fg是第S只青蛙，其中1≤S≤N.这里提出三个重要定义。

定义1：青蛙个体之间的距离采用欧氏距离来度量，定义为：

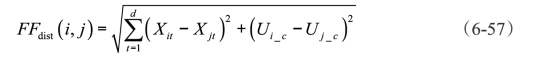
式中　Xi和Xj——分别表示两个青蛙个体（候选解）；

d——表示维数。

在定义1中，既考虑了个体之间的距离，又考虑了个体所在的子群中心点之间的距离。

定义2：青蛙个体与全局最优青蛙的最大距离定义为：

(www.xing528.com)

定义3：青蛙个体与全局最优青蛙的最小距离定义为：

本书提出了一种新的Fw更新策略，如式（6-60）和式（6-61）：

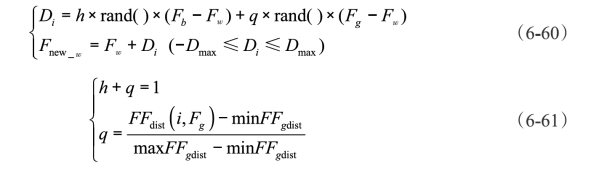
式中　h和q——分别表示局部最优解Fb和全局最优解Fg的学习因子。

当个体青蛙距离Fg越近，则h就越大，q就越小。此时，Fnew_w受Fb影响大于Fg，这样会使算法更加精确地进行局部搜索。反之，当个体青蛙距离Fg越远，则h就越小，q就越大。此时，Fnew_w受Fg影响大于Fb，这样加快收敛速度。

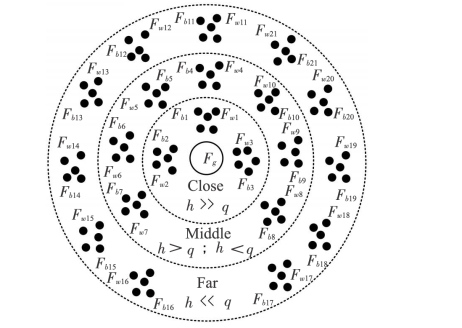
图6-11　MSFLA中Fw更新策略示意图

如图6-11所示，Fnew_w依赖于个体与Fg之间的距离，通过调节学习因子h和q达到最优更新策略。改进的更新策略不仅能够维持种群的多样性避免陷入局部最优解，还能够加快算法的收敛性。

2.基于高斯随机扰动的新解

在SFLA算法中，如果青蛙个体经过局部和全局搜索后，Fnew_w还没有原来的Fw好，就随机产生一个新解替换掉Fw，这样产生的Fw具有一定盲目性，可能会降低SFLA的收敛速度。本书结合高斯随机扰动产生一个Fnew_w替代SFLA中随机新解，具体方法如下：

式中　N（0，1）——服从均值为0，均方差为1的高斯分布；

Fw×N（0，1）——高斯分布型随机扰动项。

在原来Fw基础上加一个高斯随机扰动能够有效避免SFLA盲目搜寻。这样做一方面能够使Fnew_w不会一直陷入局部最差解。另一方面能够保证Fnew_w不会因为随机产生解，导致扰动过大使算法失真。