在分类器设计方面，样本数据是否可分是核心问题。如果样本数据都是线性可分，那么问题就很简单了。如果样本数据是非线性的，即线性不可分，则问题就比较麻烦，因为它可能造成线性分类器求不出解。在实际故障模式分类工程应用中，情况比较复杂，样本数据大都是非线性。但是线性分类的优点是不言而喻，为了解决这一问题，引入了核函数。
从空间角度分析，基于振动分析的旋转机械故障模式识别就是一个空间映射转换问题。它主要涉及四个空间，即测量空间、特征空间、决策空间以及类别空间。测量空间是指从数据采集系统获取的原始振动信号测量值所在的空间，即本书第3章所涉及内容。测量空间中的信息都是原始数据，比较复杂，为了提高故障识别准确率，为后续处理降低难度，我们根据特征提取算法对原始数据进行分析处理，将测量空间映射到特征空间，这就是本书第5章的内容。为了能够将特征空间的数据进行分类（如最小化错误分类），通常设计一个分类器使特征信息满足设定的目标函数，这样就完成了从特征空间到决策空间的映射过程，这也是本章的重要内容。一般情况下类别空间和决策空间是同一空间。
如何将线性不可分的数据样本转换为线性可分的数据样本？这就要利用核函数。它能够将低维原始输入空间的线性不可分样本数据映射到高维数据空间，转换为线性可分的样本数据，如图6-7所示。
设n为原始输入空间的维数，H为Hilbert空间，x为样本数据向量。如果存在非线性映射Φ能够将输入空间的样本数据映射到高维特征数据空间H中，如式（6-29），
使
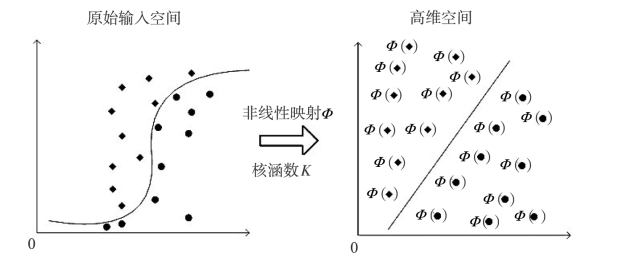
图6-7 核函数空间映射过程
在没有增加计算复杂度的前提下，通过K（xi，xj）能够将低维空间中的非线性分类数据转换到高维空间成为线性可分的数据。这时用内积K（xi，xj）替代最优分类面中的内积运算，则式（6-22）凸二次规划寻优函数变为：
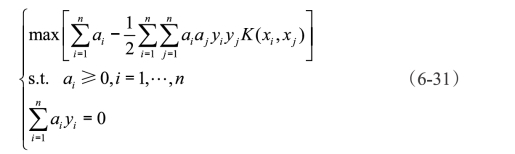
最优分类面的函数式（6-24）也相应地变成
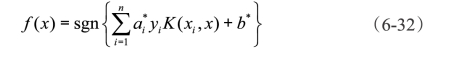
根据Hibert-Schmidt理论，凡是任意满足Mercer条件的对称函数都可以成为核函数。选择不同的内积函数能够设计不同的支持向量机，目前常用的有三种核函数：
1.q次多项式内积函数
内积核函数：
(www.xing528.com)
支持SVM的判别函数：
式中 l——表示支持矢量的个数。
2.径向基RBF内积函数
内积核函数：
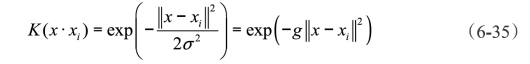
支持SVM的判别函数：
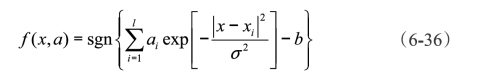
式中 σ——表示径向作用范围。
3.Sigmoid内积函数
内积核函数：
支持SVM的判别函数：
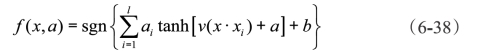
式中只有当参数v和a选取合理的值时才能够满足Mercer条件，一般选用v=2，a=1。
上述三种核函数都有其相应的参数，在实际应用中需要一些先验知识，选择不同的核函数或者相同核函数使用不同参数，都会导致分类结果大不相同。对于非线性而言，径向基RBF是最为常用核函数。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
