SVM: 基本思想与应用

支持向量机SVM是在最优分类面基础上发展起来，它的基本思想如图6-5所示。

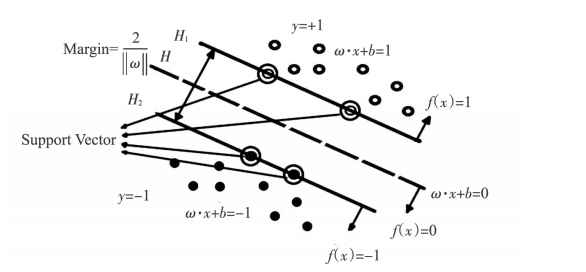
图6-5　二维两类线性可分最优分类面

图6-5中表示二维两类线性可分样本数据（分别用实心点和空心点表示），H表示为线性分类线，H1和H2分别表示穿越两类样本数据中离H最近的数据点，并且与H平行的两直线。H1和H2之间的距离称为分类间隔（Margin）。在二维空间中需要寻找的是最优线性分类线，一方面它必须准确地划分两类样本数据，使数据样本的训练错误率为零，即经验风险最小；另一方面它还要使分类间隔为最大，这样才能保证置信范围最小，即真实风险最小。上述讨论范围限于二维空间，以此类推到高维空间中，最优分类线则变成了最优分类面。

如果两类线性可分的样本数据集为（xi，yi），i=1，…，n，n ∈Rd，yi∈｛+1，-1｝，线性判别函数为：

其对应的分类面方程为：

将式（6-15）进行归一化处理，使两类中的所有样本都满足|f（x）|≥1，从图6-5可以清楚看到|f（x）|=1是距离分类面最近的样本集合。如果要求式（6-16）对全部样本数据进行正确分类，就要满足下列不等式：

求解最优分类面可以转化为约束优化问题，即在式（6-17）约束下，求式（6-18）的最小值：

为求得最小值可以定义如下Lagrange函数

(www.xing528.com)

其中ai≥0表示Lagrange系数，为求式（6-19）最小值，就得分别对变量ω、b和ai求偏微分方程并且令其方程为零求解：

由式（6-20）可推导出

根据式（6-17）和式（6-21），可将问题转化为如下凸二次规划寻优对偶问题：

式中sgn为符号函数，定义如下：

当0＜ξi＜1时，表示其对应的样本数据xi分类正确。当ξi≥1时，表示分类错误。当ξ=0时说明样本数据中没有离开群的点，即离群点（Outlier）。如图6-6所示，图中可以清楚看到，在H1和H2中分别都有一个来自H2和H1的离群点，离群点会给分类带来损失。但是承受这些损失带来的好处就是分类面不必为了满足准确分类的要求向这些点移动，从而保证了分类间隔最大化。为了能够准确度量这些损失给分类器带来的影响程度，引入了两个参数进行量化，一个就是上面提到的松弛因子ξ，另外一个就是惩罚因子C（Cost）。这样，目标函数（6-18）就变为：

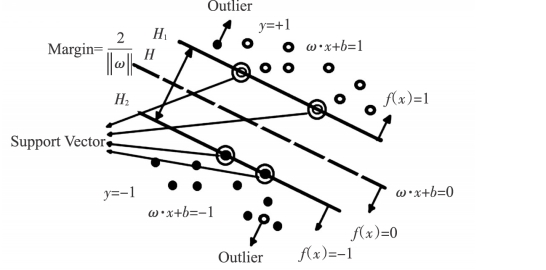
图6-6　离群点示意图

上述在线性不可分的情况下求得的最优分类面称为广义最优分类面。