小波基函数的应用与特点

通过上述各小节分析可知小波基是小波分析中的核心问题。针对不同的信号特征选择合适的小波基是小波变换的关键。同样的信号采用不同小波基分析处理可能得到完全不同的效果。选取小波基函数ψ（t）主要考虑其紧支性、对称性、正则性和消失矩。

1.紧支性

小波基函数是能够迅速衰减的振荡性短波。所谓衰减是指当t→∞时，ψ（t）的函数值能够迅速衰减为零。为了使小波时域局域化特性好，就必须是选择衰减快紧支宽度窄的小波基。在Mallat快速小波分解中，滤波器组滤波过程中存在截断误差。如果ψ（t）具有紧支性，则能够有效避免这一误差。在理想状态下，希望小波基在时域和频域上都具有紧支性，遗憾的是这很难办到。因此一般情况下偏重于小波基在时域下的紧支性。

2.对称性

对称性不仅能够构造出具有紧支的正则性，还能构造出具有线性相位的小波基函数。小波基的对称性对需要进行信号重构的场合来说意义重大。但是在振动信号分析中只对信号进行分解，不进行重构，因此对小波基的对称性要求不是十分严格。

3.正则性

小波基ψ（t）是否可微是正则性的表现形式。在实际工程应用中，正则性是对小波函数光滑程度的量化指标。正则性阶数越大说明小波基ψ（t）就越光滑，相应的，它在频域上的能量就更集中。对于正交小波而言正则性与消失矩阶数是互相有着密切联系的，正则性越大则消失矩越高。

4.消失矩

小波逼近光滑函数的收敛性是由消失矩决定的。它能够表示信号经过小波变换后能量集中的程度。采用消失矩阶数大的小波基进行信号分解后，小波变换的系数就越小，信号的能量就越集中。在小波快速分解算法中使用了滤波器的概念，消失矩阶数越大，它所对应的滤波器就越平坦。同时小波基函数的振荡性很强。因此小波基的消失矩需具有足够高的阶数，当然消失矩也不是越大就越高，太大的消失矩阶数会导致分析结果模糊。

考虑到机械设备的振动信号的特征，选择小波基时应该尽量选择消失矩阶数高、正则性大以及紧支撑区间大的小波基函数，对于对称性可以适当放宽要求。

本书介绍几种常见的小波函数：

1.Harr小波

Harr小波在时域范围内不具有连续可微特性，所以其小波特性表现得不是很好。但是Harr小波是目前最为简单的小波，所以一般作为展示小波原理性范例使用。Harr小波图像如图5-8所示。

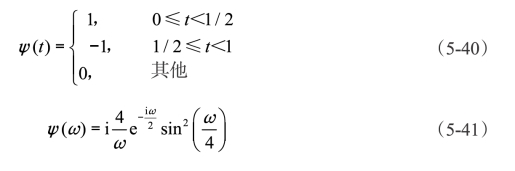
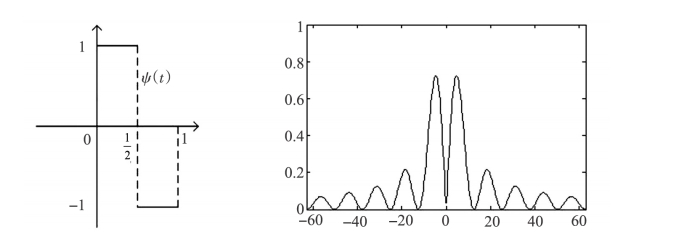
图5-8　Harr小波(www.xing528.com)

2.Daubechies小波

Daubechies小波简称为dbN，其中N表示消失矩的阶数。前面提到的Harr小波就是dbl小波，除了dbl外，Daubechies小波函数没有一个明确的表达式。它属于紧支撑正交小波，阶数越高越平滑。Daubechies小波图像如图5-9所示。

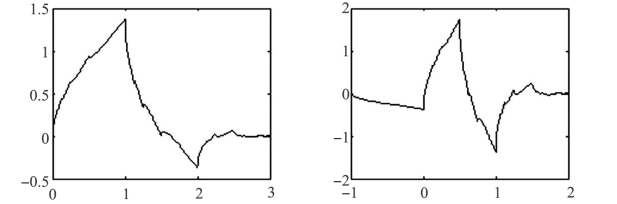
图5-9　Daubechies小波

3.Morlet小波

Morlet小波是一个较为常用的小波，它没有尺度出数，虽然它不具有紧支性，但Morlet小波，具有快速衰减的特性。它是Gabor小波的一个特例。Morlet小波图像如图5-10所示。

图5-10　Morlet小波

4.Gauss小波

Gauss小波是Gauss函数的一阶导数（Marr小波是Gauss函数的二阶导数），它具有很好的时间频率局部化特性，一般适用于边缘特征提取。

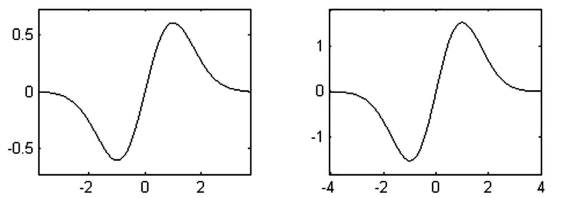
图5-11　Gauss小波

小波基的选取将直接对实验分析结果产生影响。因为旋转机械产生的振动信号是非平稳信号，信号包含瞬态和突变成分，在瞬态和突变的频率成分中波形是不规则的，所以选用小波基时必须考虑紧支性。通过比较，本书选用dbN系列的小波基，N为消失矩的阶数，N越大小波变换后表现出的高频细节信号能力越强。实验用的轴流泵转速为960r/min，它的基频为16Hz，故障系统主要分析其100Hz左右的频段，属于低频分量并且局部波形不是很光滑，考虑上述因素后小波基的消失矩不能太高，也即是正则性不能太好。另外，为了更好地反映出信号的局部化特征，小波基的紧支撑区间应该适当增大，dbN系列小波的支撑长度是2N-1。综上所述，本书选用db4作为小波基。