小波信号分解与重构技术

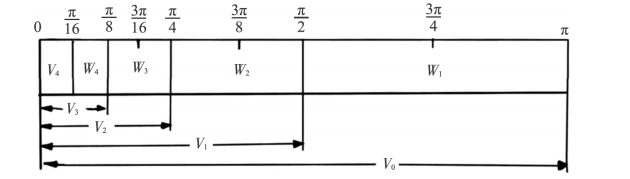
图5-6　频带划分

信号就被分解为高频信号空间Wj和低频信号空间Vj，Wj代表信号细节（Details）部分，Vj表示信号近似（逼近）部分（Approximations）。

信号是由多种频率成分构成，有高频也有低频。相对而言，信号中的低频率分量比高频率分量更加重要，低频成分是信号的特征标识别，而高频成分起修饰作用。例如声音信号，如果将它的低频分量去掉，我们什么都听不出来；如果将它的高频分量去掉，声音信号会发生改变，但是内容我们还是能够听出来。

那如何才能将原始信号分解为低频空间和高频空间呢？小波变换中通过滤波器组实现，滤波器组由低通滤波器（Low-Pass Filters，简称LPF）和高通滤波器（High-Pass Filters，简称HPF）构成。因为旋转机械故障特征提取时主要涉及小波分解技术，所以本书就小波信号分解过程进行详细说明：

（1）原始信号S与分别与低通分解滤波器h和高通分解滤波器g进行卷积运算，获取S中的低频分量Aj和高频分量Dj。

（2）分别对Aj和Dj进行下抽样（每隔一个元素抽取一个数据，如只要信号中的偶数项）获得离散低频（逼近）系数cAj和离散高频（细节）系数cDj。

（3）对cAj作为原始信号重复步骤（1）和（2），可计算出Aj+1、Dj+1和cAj+1、cDj+1。

（4）重复（1）～（3）步骤，可以得到一系列cA和离散高频（细节）系数cD。

将小波分解后，还可以利用小波分解系数还原出原始信号，即小波重构（Wavelet Reconstruction），也称为小波合成（Wavelet Synthesis）。由小波分解得到的cA和cD系数可以重构出原始波形。重构过程就是分解过程的逆过程：

（1）cA和cD经过上抽样（在两个元素之间内插入一个零值）分别与低通重构滤波器h*、高通重构滤波器进行卷积获得低频分量Aj+1和高频分量Dj+1。

（2）将Aj+1与Dj+1相加得到Aj，再将Aj与Dj相加得到Aj-1，以此类推，最后A1与D1相加获得原始信号S。

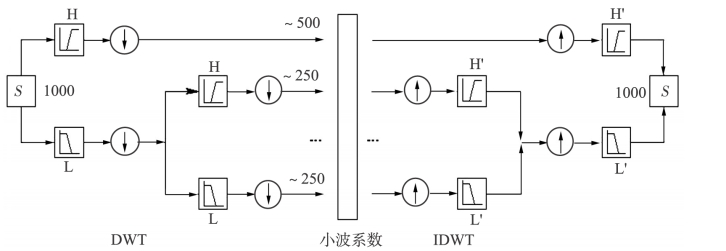
图5-7　小波分解和重构的示意图(www.xing528.com)

通过上述分析可知，滤波器组能够实现信号的分解和重构，这种思想被引入到快速小波变换（Fast Wavelet Transform，简称FWT）中，也称Mallat算法。小波变换是运用信号和小波基函数进行内积计算，而FWT是运用信号和滤波器组进行卷积计算。这样计算量大大降低，FWT算法类似于FFT在Fourier变换中的地位。FWT中最重要的就是滤波器组的选择，为了实现FWT，通常需要采用正交镜像滤波器组，它们的计算与前面章节提到的尺度函数φ以及小波函数ψ（t）有关，与尺度j无关。若h表示离散低通分解滤波器，g表示离散高通分解滤波器，h*表示离散低通重构滤波器，g*表示离散高通重构滤波器，则对一个小波基而言，它的尺度函数φ和小波函数ψ是确定的，且存在一个双尺度关系式：

根据式（5-33）可以求出h*，再根据下列方程式可以依次求出h、g和g*：

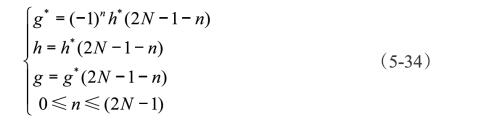
有了h、j、h*和g*就能够求出尺度系数cA和cD。如果Pjf（t）表示f（t）∈L2（R）在空间Vj中的正交投影，则

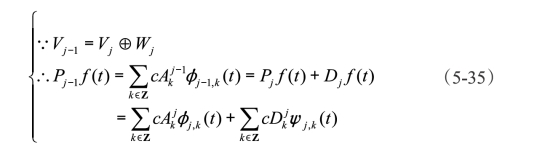
根据φ和ψ的平移性和伸缩正交性，可从式（5-35）分别推导出以下等式：

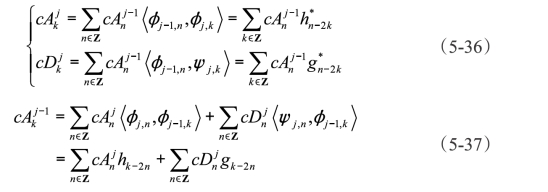
式（5-36）和（5-37）就是著名的Mallat小波分解算法和Mallat小波重构算法，它们统称为一维信号的离散小波变换Mallat算法。cA是离散近似信号的系数，cD表示离散细节信号系数。可以看出，cD实质上就是小波变换所得到的系数WTf（j，b）。Mallat算法的卷积表示方式如下：

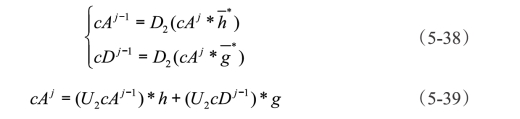
式中　D2——表示二元下抽样；

U2——表示二元上抽样；

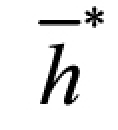——表示h的共轭反转。

从上述描述可以知道，Mallat算法一方面将小波多分辨分析和滤波器之间的关系进行了剖析；另一方面通过卷积实现了小波快速变化。因此它在小波研究中的地位相当高。