如何计算滚珠丝杠副的力并选择适合驱动马达？

（1）轴向负载F_a

图10-4所示为滚珠丝杠副受力图。

对图10-4a所示的丝杠加一转矩T后，在圆周力F_r的作用下，与螺母联接的滑台及工件将被驱动作轴向运动。设轴向负载F_a集中作用于螺旋槽工作面上，则丝杠螺旋面推动螺母组件运动的推力方向必为沿着接触点的法线方向，此力称为法向力F_N。F_N和摩擦力f合成为全反力F_R。设螺母组件沿螺旋槽作等速运动，在轴向负载F_a、圆周力F_r和全反力F_R的共同作用下处于平衡状态。由力的封闭三角形可得正向轴向负载为

F_a=F_r／tan（λ+ρ） （10-1）

对于图10-4b所示的反方向受力的滚珠丝杠副，同理，由力的封闭三角形原理可得反向轴向负载为

F_a=F_r／tan（λ-ρ） （10-2）

两式中 F_a——沿丝杠的轴向负载（N）；

F_r——加于丝杠的圆周力（N）；

ρ——丝杠副的摩擦角，ρ=arctanμ，μ为摩擦因数；

λ——丝杠的螺旋升角，tanλ=P_h／（πd₀），P_h为丝杠副的导程，d₀为丝杠副的螺纹中径，对于滚珠丝杠副，d₀为在螺旋滚道径向滚珠中心的径距。

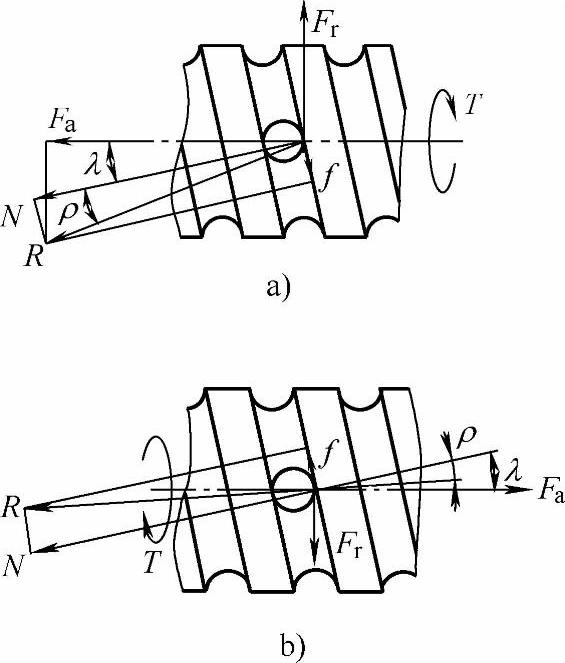
图10-4 滚珠丝杠副受力图

a）工作方向（正向）受力图 b）反向受力图

（2）负载转矩T_L

对于图10-4a所示的工作方向负载，当丝杠转动时，为克服丝杠的轴向负载F_a所需的转矩为

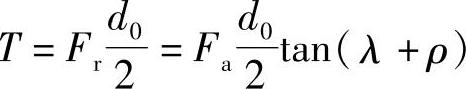
因丝杠转动时，转矩T所作的功为

W₁=2πT=F_aπd₀tan（λ+ρ）

而丝杠转动一周时，驱动负载移动的距离为导程P_h，所以移动负载所作的功为

W₂=F_aP_h=F_aπd₀tanλ

因此，丝杠传动的效率为

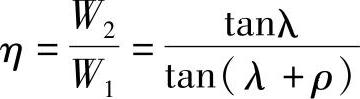
所以考虑传动效率时，滚珠丝杠的负载转矩为

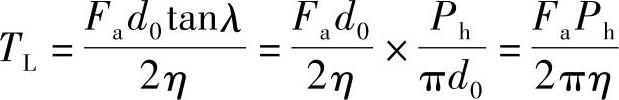
对于滚珠丝杠对反向负载的自锁性能，由式（10-2）可知，加于丝杠的反向圆周力为F_r=F_atan（λ-ρ），于是可得

1）当λ＜ρ时，F_r＜0，能自锁。

2）当λ＞ρ时，F_r＞0，不能自锁。

对于钢-钢组合滑动摩擦螺旋副，摩擦因数μ=0.12～0.17，摩擦角ρ=arctan（0.12～0.17）=6.8°～9.6°。所以这种螺旋副能自锁。

对于滚珠丝杠副的滚动摩擦螺旋副，摩擦因数μ=0.001～0.003，摩擦角ρ=arctan（0.001～0.003）=0.057°～0.167°。实际上，滚珠丝杠的螺旋升角λ大于2°，所以不能自锁。

为了防止滚珠丝杠副不能自锁而产生逆转动，特别是当用于垂直方向传动时，如果部件重量没有平衡，则会因其自重作用而发生逆转。所以要采取防逆转措施，如采用单向联轴器或反制动装置等。

（3）预载摩擦转矩T_P

为了消除滚珠丝杠副的轴向间隙，以免产生反向运动回差，需通过螺母对丝杠施加轴向预载。因此，在计算滚珠丝杠传动转矩时，需考虑因预载力所产生的摩擦转矩。预载摩擦转矩T_p计算式如下

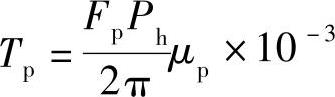
式中 T_p——预载产生的摩擦转矩（N·m）；

P_h——导程（mm）；

μ_p——螺母预载后丝杠副的摩擦因数，通常取μ_p=0.1～0.3；

F_p——对丝杠副的预紧力（N）。

对丝杠副的预紧力F_p可取轴向工作负载的1／3，即F_p=F_a／3。

若轴向工作负载未能确定，可按下式计算预紧力

F_p=ξC_a

式中 C_a——滚珠丝杠副的额定动负载（N），可在产品说明书中查到；

ξ——与驱动负载有关的系数，可按如下选取：轻负载ξ=0.05，中负载ξ=0.10，重负载ξ=0.15。

（4）加速传动系统运动构件所需的惯性转矩T_J

传动系统如果要求频繁起动、停止和响应时间较短，则要考虑由于系统的惯性所引起的惯性转矩。

由负载、传动链和电动机转子的惯性所引起的、折算到电动机输出轴的惯性转矩T_J按下式计算

T_J=（J_L+J_M）ε

式中 T_J——加速传动系统所需的惯性转矩（N·m）；

J_L——系统运动构件折算到电动机输出轴的转动惯量（kg·m²）；

J_M——电动机转子转动惯量（可在产品说明书查得）（kg·m²）；

ε——电动机输出轴的角加速度（rad／s²）。

系统运动构件折算到电动机输出轴的转动惯量J_L，可根据电动机类型和有关参数按下式计算

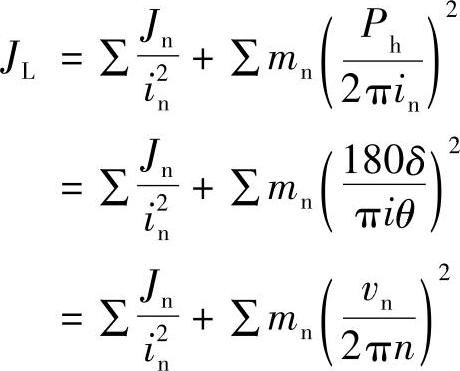
式中J_n、i_n——系统各转动构件的转动惯量（kg·m²）和相应传动比；

m_n、v_n——各直线运动构件的质量（kg）及其移动速度（m／mjn）；

P_h——丝杠导程（m）；(www.xing528.com)

δ——每一脉冲工作台的移动量（m）；

θ——每一脉冲电动机的转角（°）；

n——电动机转速（r／mjn）。

现以图10-5为例，计算系统运动构件折算到电动机输出轴的转动惯量。由上式，有

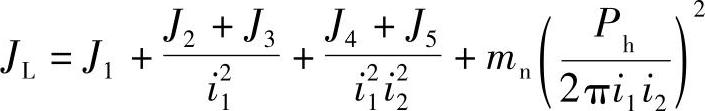
式中 J₁、J₂、J₃、J₄——齿轮1、2、3、4的转动惯量（kg·m²）；

J₅——丝杠的转动惯量（kg·m²）；

m_n——工件、工作台和螺母的总质量（kg）；

P_h——丝杠导程（m）；

i₁、i₂——第1、2级传动比。

所以图10-5所示传动系统的惯性转矩T_J为

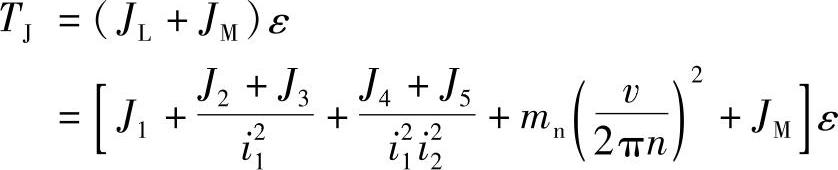
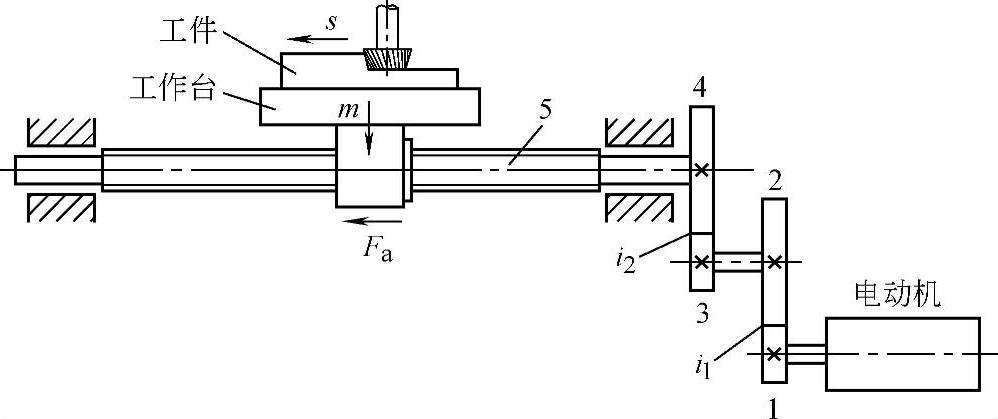
图10-5 典型齿轮-滚珠丝杠传动系统

如果要求在t_a秒（几分之一秒）内达到电动机额定转速n，则角加速度ε可按线性规律计算，即

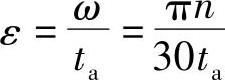
式中 ω——电动机轴角速度（rad／s）；

n——电动机额定转速（rad／mjn）；

t_a——加速时间（s），t_a≈3～4t_m，t_m为电动机时间常数，可查产品说明书，t_a也可按需要设定。

圆柱齿轮和丝杠的转动惯量可按圆柱体转动惯量计算，于是一个圆柱齿轮的转动惯量为

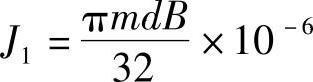
式中J₁——齿轮转动惯量（kg·m²）；

m——齿轮质量（kg）；

d——齿轮分度圆直径（mm）；

B——齿轮的齿宽（mm）。

丝杠的转动惯量为

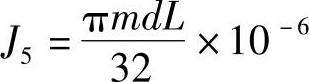
式中 J₅——丝杠转动惯量（kg·m²）；

m——丝杠质量（kg）；

d——丝杠公称直径（mm）；

L——丝杠长度（mm）。

（5）电动机的选择

滚珠丝杠传动系统中电动机的总驱动转矩T_M由如下三部分组成：

1）滚珠丝杠的负载转矩T_L，用以驱动加于丝杠的外部负载所需的转矩。

2）预载产生的摩擦转矩T_p，用以克服因螺母对丝杠预载力而产生的内部摩擦力所需的转矩。

3）加速传动系统所需的惯性转矩T_J，用以克服传动轮系的齿轮、滚珠丝杠副、工作台及工件等的惯性所需的转矩。

电动机总驱动转矩T_M的计算式为

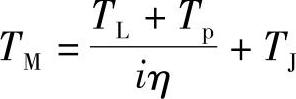
传动链的总效率η通常为η=0.95～0.98。

传动比i的确定，应考虑电动机转子的转动惯量、额定转速、负载轴及传动系统的转动惯量和负载轴转速这四个量的匹配。它们应有如下的关系

J_Mn_M=J_an_a最佳总传动比为

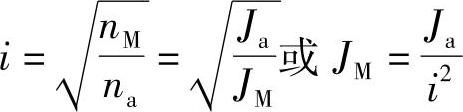
式中 i——电动机输出轴至生产机械负载轴的最佳总传动比；

n_M——电动机额定转速（r／mjn）；

n_a——负载轴的转速（r／mjn）；

J_M——电动机转子的转动惯量（kg·m²）；

J_a——负载轴及传动系统的转动惯量（kg·m²）。

上式表明，其总传动比的最佳值，是使折算到电动机轴上的负载转动惯量等于电动机转子的转动惯量。符合此原则时，电动机的驱动力矩有一半用于加速负载，另一半用于驱动电动机转子。这就是按转动惯量最小原则确定最佳总传动比法。所谓最小转动惯量，是指传动链中各运动构件的转动惯量折算到电动机轴上的等效转动惯量为最小。因惯性小，则传动快捷灵敏，定位精确和稳定。对于需要经常作正反转和时停时动的传动系统，特别是小功率伺服传动系统，更需按此原则来确定传动链的总传动比和分配各级传动比，以取得最佳的传动效果。

选择电动机时的注意事项为：

1）惯性要匹配，通常电动机的转动惯量应满足J_M=（1～4）J_L。

2）电动机的额定转矩T₀必须大于总负载转矩T_M，即T₀＞T_M。

3）电动机转速为n（r／mjn），加于电动机输出轴的负载转矩为T_M（N·m），则所需电动机功率P（W）为

P=（1.05～1.10）30T_Mn／π