正切和正割机构的工作原理及应用

图6-25所示是最基本的正切机构。摆杆1槽内的可移动滑块2与顶杆3铰连。摆杆绕O点摆动α角，顶杆的位移y按正切规律变化。即

y=ltanα

若输入角从OY轴起算，则为余切机构。

这种机构的缺点是滑动摩擦大，巨在大角度变化时会引起正切值的迅速增大而使机构难以调节。所以一般限于在30°～45°范围内工作。

图6-21所示的正弦尺调节机构很容易改为正切机构。只要把销子2固定在滑尺3上，而在旋钮上开槽，即可使滑尺的位移量x按正切规律变化。

图6-26所示是类似于正切机构的正割机构，其输出位移量为

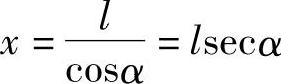
若转角α由OY轴起算，则按余割机构规律变化，其输出位移量为

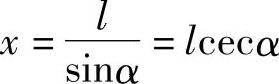
图6-27所示是能同时实现正切和正割组合运算的三角函数机构。其输出位移量为

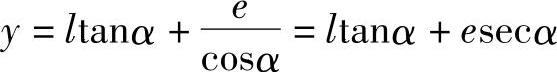
由上式可知，当e=0时，则为图6-25所示的正切机构；当l=0时，则为图6-26所示的正割机构。

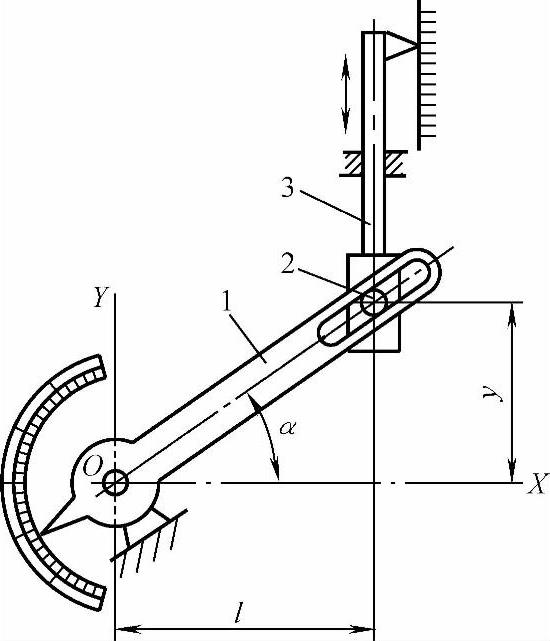
图6-25 正切机构

1—摆杆 2—可移动滑块 3—顶杆(www.xing528.com)

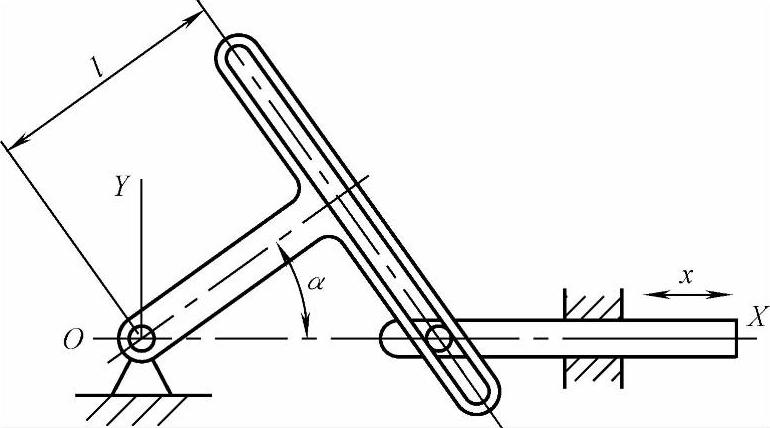
图6-26 正割机构

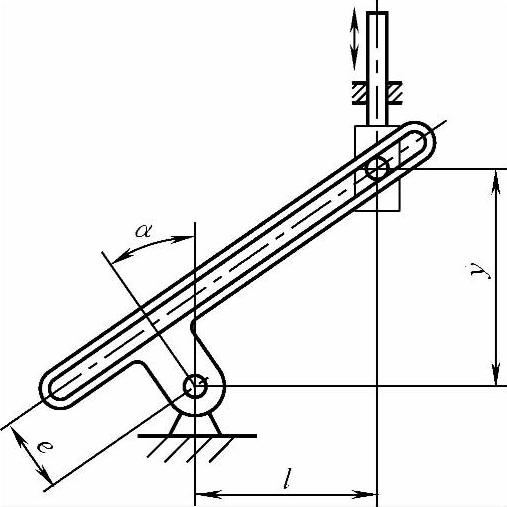
图6-27 正切和正割组合机构

图6-28 具有两个输入变量的正切机构

1—轴 2—螺杆 3—移动架 4—带齿条的滑块 5—圆盘 6—长齿轮 7—蜗杆 8—滑块 9—销子

以上的三角函数机构均只含有一个变量α，结构比较简单。图6-28所示是具有两个输入变量的较复杂的正切机构。圆盘5兼作蜗轮，在蜗杆7的传动下绕固定轴心O转动。圆盘开有一个导槽，滑块8可在槽内滑动。带齿条的滑块4可在移动架3的槽内滑动。滑块4和滑块8通过销子9铰连于A。圆盘水平中心线与移动架的中心线垂直相交于B。于是直角三角形OAB的两直角边OB和AB的长度可改变。

蜗杆驱动圆盘的转角α为输入转角量；轴1及两对锥齿轮副驱动两螺杆2，使移动架对圆盘中心产生的位移量x为输入线性量。两个输入量的合成结果使A、B两点的位置改变，于是有与之相应的输出位移量y。由三角形可得它们的关系为

y=xtanα

机构也可用滑块4的齿条与长齿轮6的啮合传动，把输出位移量y变为输出回转量α_y。

这种机构也可看成是乘法机构。其输出就是位移变量与转角的正切之乘积。

应注意的是，转角α只能在0°～50°范围内变化，因为转角过大将使正切值急剧增大，以致机构卡死。