正弦余弦机构的构造与应用

正弦和余弦机构通常可用曲柄连杆、槽架、齿轮和偏心轮等构件组成。

（1）曲柄连杆式正（余）弦机构

图6-19所示是曲柄连杆式正（余）弦机构的基本原理。设l₁为曲柄长度，l₂为连杆长度，转动曲柄以转角α作为输入量，则可得到按该角的正弦或余弦变化规律的直线运动输出量x或y。由图6-19可知

x=l₁cosα

y=l₁sinα

（2）槽架式正（余）弦机构

在某些自动化仪表中，有一种如图6-20所示的槽架式正（余）弦机构。圆盘1转动，通过销子2推动槽架3作直线位移运动。销子的角位移量α是输入量；槽架的滑尺所作的直线位移x是输出量，它遵循正（余）弦规律变化。即

x=rsinα

或 x=rcosβ

因α与β互为余角，所以正弦值和余弦值同时出现。

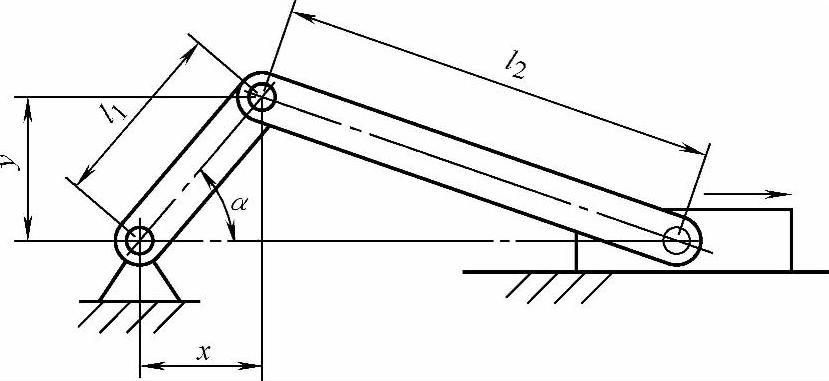
图6-19 曲柄连杆式正（余）弦机构的基本原理

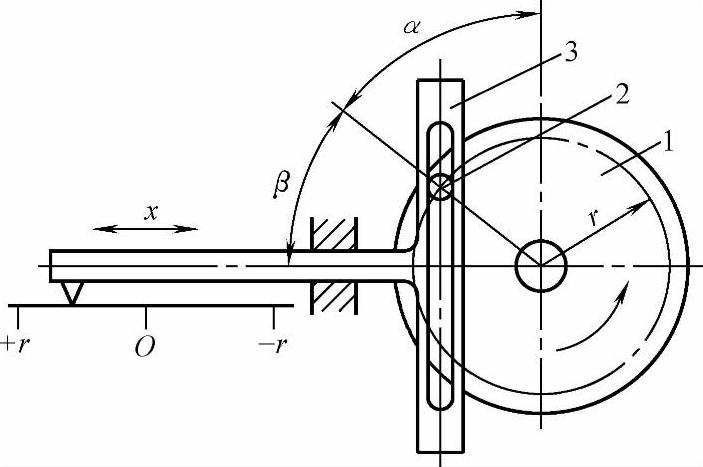
图6-20 槽架式正（余）弦机构

1—圆盘 2—销子 3—槽架

根据上述机构原理可制成如图6-21所示的正弦尺调节机构。滑尺3开有槽，旋钮1装有销子2。销子与槽滑动配合。销子的旋转半径为r，当转动旋钮时，滑尺的直线位移量x则在±r范围内按正弦规律变化。

为了在同一转角中同时得到其正弦和余弦两个函数值，可采用双槽架机构（见图6-22）。

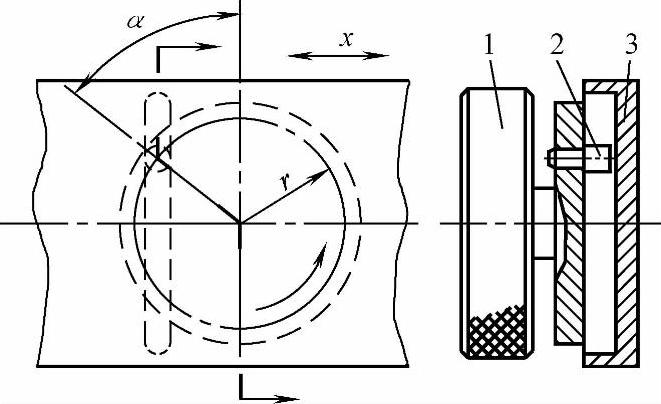
图6-21 正弦尺调节机构

1—旋钮 2—销子 3—滑尺

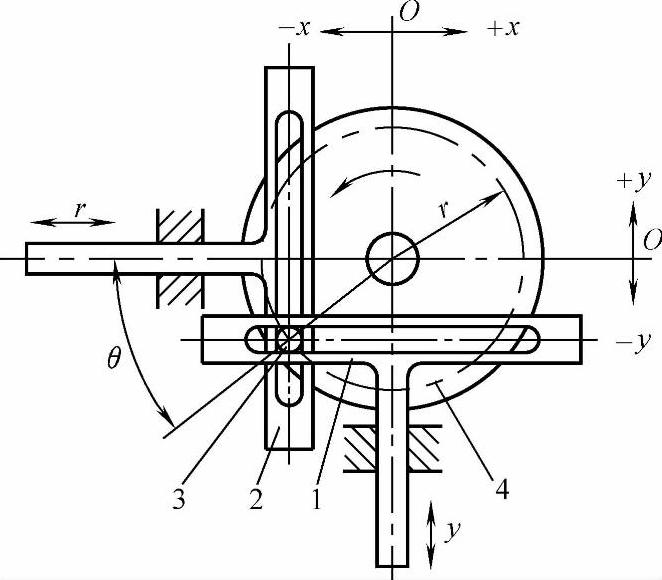
图6-22 双槽架正（余）弦机构

1、2—槽架 3—销子 4—圆盘

机构的两个槽架1和2用同一圆盘4上的销子3驱动。这样就可以把圆盘某一个输入转角量同时转换为按正弦和余弦规律变化的两个输出位移量。槽架1和2各输出端的位移量y和x分别为

y=rsinα

x=rcosα(www.xing528.com)

（3）行星齿轮式余弦机构

图6-23所示是内啮合行星轮系余弦机构。内齿轮1固定不动，与之啮合的行星齿轮3在转臂2的驱动下既作自转又绕内齿轮作公转。行星齿轮的节径正好等于内齿轮的节圆半径。在此条件下，行星齿轮节圆上的某一点（销子4）在传动过程中所描出的轨迹是一条特殊的内摆线：直线。而巨这销子在此直线上的运动是按余弦规律变化的。

由运动学分析可知，内摆线的运动方程为

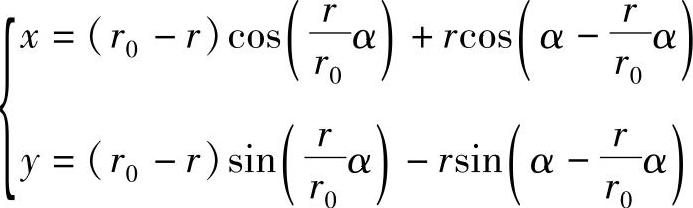
式中r₀——内齿轮节圆半径；

r——行星齿轮节圆半径；

α——转臂的输入转角。

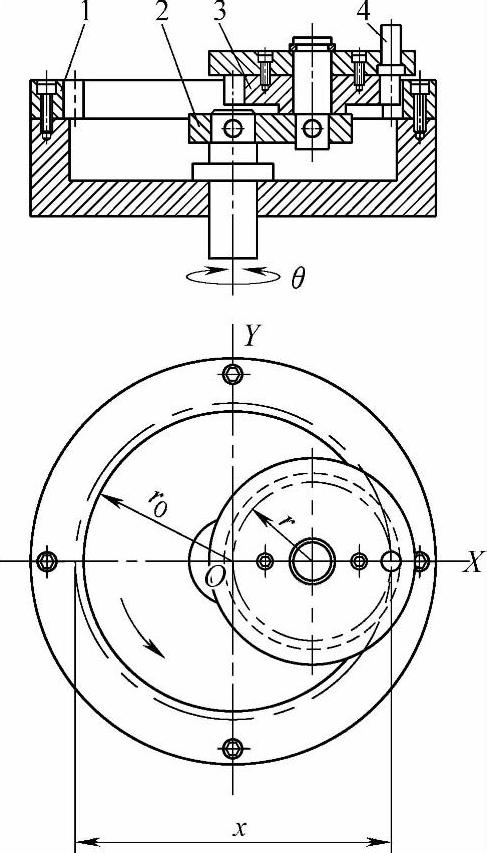
图6-23 内啮合行星齿轮式余弦机构

1—内齿轮 2—转臂 3—行星齿轮 4—销子

当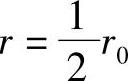时，上式变为

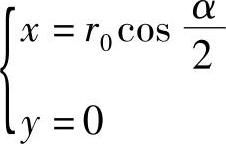
上式表明，这种机构的销子4按余弦规律作直线运动。这种机构的优点是没有槽架式机构的那种滑动摩擦，所以运动平稳。

（4）偏心轮式正（余）弦机构

图6-24所示是利用偏心轮的转动来推动从动杆作直线运动的正（余）弦机构。这种直线运动近似地按正弦规律变化。用公式表示为

y=esinα

式中 e——圆盘凸轮的几何中心对其旋转中心的偏心量；

α——圆盘凸轮的转角。

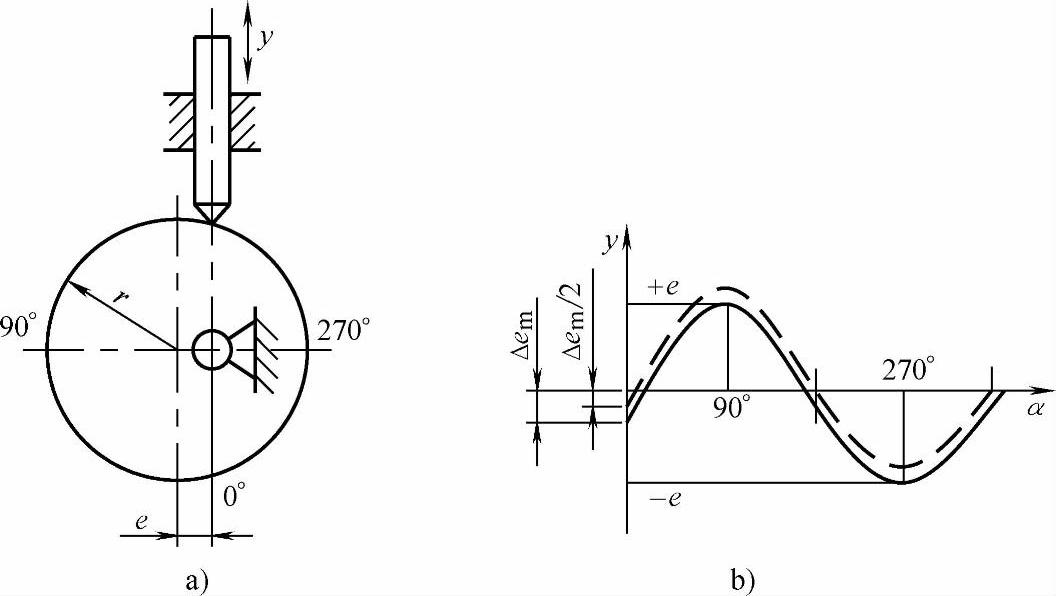
图6-24 偏心轮式正（余）弦机构

a）结构图 b）输入输出量曲线图

这种机构的输出值有一定的误差，误差的大小如图6-24b所示。在0°和180°有最大误差Δe_m，其值为

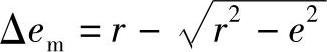
式中 r——圆盘凸轮半径。

由上式可见，若增大圆盘凸轮半径r，减小偏心e，则可使误差减小，但误差仍存在。如图6-24b所示，当把最大误差减小到Δe_m／2时，曲线仍有失真。