基于相似三角形原理的杠杆式乘法机构及其应用

杠杆式乘法机构是基于相似三角形原理。图6-10所示机构由杠杆1、2和3及两个滑块组成。根据相似三角形关系，有

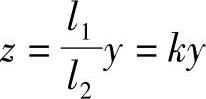
式中，k=l₁／l₂是比例系数，为不变因子。y是输入量，为可变因子。可见，这种机构可实现常量与变量相乘的运算。

为防止机构发生卡死，杠杆1对O-x轴的夹角应在45°范围内。

如果把图6-10所示机构的距离l₁设计为可变量，则有如图6-11所示的两个变量相乘的杠杆式乘法机构。这时杠杆2的位置x可用螺杆4来改变。同样按相似三角形原理得两输入变量x和y与输出量z的关系为

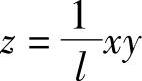
式中，l是杠杆1的摆动中心至杠杆3轴线的距离，称之为结构常数。

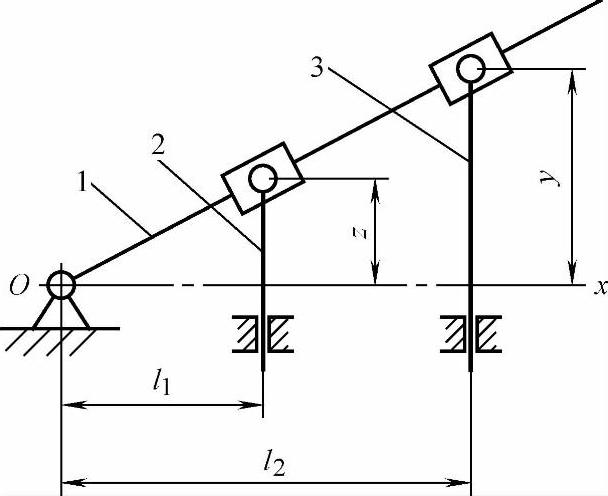
图6-10 常量与变量相乘的杠杆式乘法机构

图6-11 两个变量相乘的杠杆式乘法机构

1、2、3—杠杆 4—螺杆

图6-12所示机构是图6-11所示机构的另一种形式，称为槽架式杠杆乘法机构。图6-12a为其结构图，其特点是三个槽板相交于动销B，两对锥齿轮2和两根螺杆3把回转运动变为槽板6沿x方向的移动，这是输入变量x。绕固定点C摆动的槽板5与齿条4铰连于A，齿轮1和齿条4的驱动，使点A沿y方向移动，这是输入变量y。槽板7在动销B的带动下作y向移动，这就是输出量z（或是通过槽板7上的齿条传给齿轮8以转角形式输出）。

由位移量x、y和z所构成的两个相似直角三角形，根据上述关系式有如下三种特殊情况：

1）若动销B与固定销C重合，而槽板6固定不动（x=0）（见图6-12b），则不管槽板5如何运动，槽板7均不会移动（z=0）。

2）若动销B与固定销C重合，而槽板5固定不动（y=0）（见图6-12c），则不管槽板6如何运动，槽板7也不会移动（z=0）。

图6-12 槽架式杠杆乘法机构

a）结构图 b）、c）、d）输出量为零的三种情况(www.xing528.com)

1、8—齿轮 2—锥齿轮 3—螺杆 4—齿条 5、6、7—槽板

3）只要槽板5的槽孔轴线正好在零线（O-O位置），不管槽板6在何位置，槽板7也不会有输出（见图6-12d）。

从理论上讲，除法机构可用上述乘法机构的逆运动来实现，但实际应用中会受到一定的限制。因为如果作除法机构，分母趋近于零会使其商变得很大。这时只要有一个很小的输入变化量，就会引起一个很大的输出量，甚至远超出杠杆的变化范围。而巨输入转矩也很大，机构容易磨损和卡死。

但是，通过一定的方法可用一般的乘法机构来进行除法运算。比如，要实现z=x／y的除法运算，可把式子看成是z=（1／y）x。这就是求y的倒数与x乘积的问题。若1／y可求，则其积可用乘法机构运算。这称为倒数求商。

这种方法的关键是要设计一个倒数机构。图6-13所示是一个简单的倒数机构，它由两个滑块1和2以及两臂成90°角的槽板式杠杆3组成。

当滑块1输入量为y时，杠杆3绕O点摆动，使滑块2有相应的输出量R，R与y的倒数成比例。由相似直角三角形△OCA和△ODB可知

即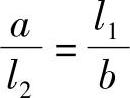

所以

因为l₁和l₂可看成是输入量y和输出量R，所以上式为

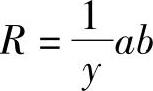
这就是倒数机构的运动公式。

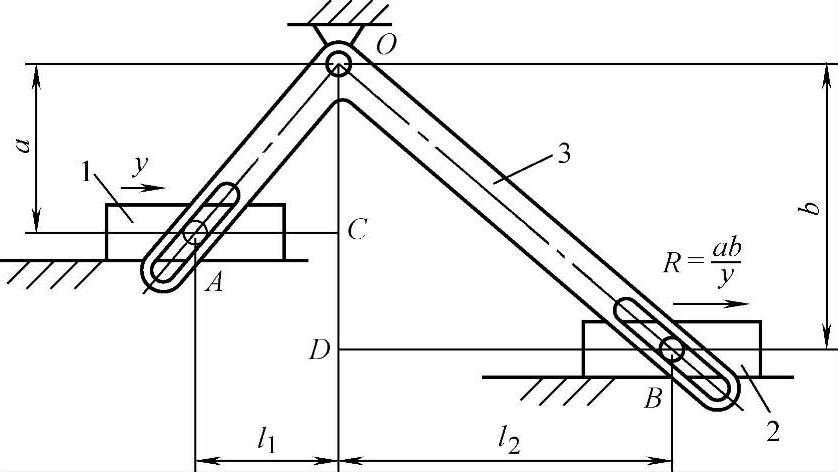
图6-13 倒数机构

1、2—滑块 3—槽板式杠杆

利用倒数机构与上述的乘法机构结合起来，便可成为一个求商的乘法机构。这时，倒数机构的输出量R就是乘法机构的输入量之一。其关系式为

z=Rx

式中 R——随输入变量y而改变的可变比例系数，R=ab／y。